7.一矿井深125 m，在井口每隔一段时间落下一个小球，当第11个小球刚从井口开始下落时，第1个小球恰好到达井底，则(1)相邻两个小球下落的时间间隔是______s；(2)这时第3个小球与第5个小球相距______.(g取10 m/s²)

[解析] 下落时间t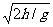＝＝5 s，则时间间隔为0.5 s，由位移公式得s₂－s₅＝25 m

[答案] 0.5　 35 m

6.某人用手表估测火车的加速度.先观测3 min，发现火车前进540 m；隔3 min后又观察1 min，发现火车前进360 m.若火车在这7 min内做匀加速直线运动，则火车的加速度为

A.0.03 m/s²　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 B.0.01 m/s²

C.0.5 m/s²　　　　　　　 　　　　　　　　　　　　　　　　　　　　　 D.0.6 m/s²

[解析] 解法1：对前3min内s₁＝v₀t₁+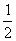at₁²

对最后1min内s₂＝［v₀+a(t₁+2)］·t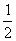₂+at₂²

代入已知数据联立解得a=0.01 m/s²

解法2：前3 min中间时刻的瞬时速度为

v₁=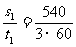 m/s=3 m/s

后1 min的中间时刻的瞬时速度为

v₂=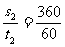 m/s=6 m/s

加速度为　 a=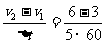 m/s²=0.01 m/s²

[答案] B

5.一匀变速直线运动的物体，设全程的平均速度为v₁，运动中间时刻的速度为v₂，经过全程位移中点的速度为v₃，则下列关系正确的是

A.v₁＞v₂＞v₃　　　　　　　　 　　　　　　　　　　　　　　　　　　 B.v₁＜v₂=v₃

C.v₁=v₂＜v₃　　　　　　　　 　　　　　　　　　　　　　　　　　　　 D.v₁＞v₂=v₃

[解析] 根据匀变速直线运动的规律知，v₁=v₂，由v-t图象不难得出，无论物体做匀加速直线运动，还是物体做匀减速直线运动，位移中点的速度都比中间时刻的速度大，即v₃＞v₂(如图a、b所示)

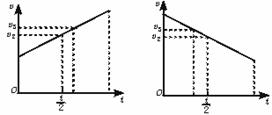
图a　　　　　　　　 图b

[答案] C

4.由高处的某一点开始，甲物体先做自由落体运动，乙物体后做自由落体运动，以乙为参考系，甲的运动情况是

A.相对静止

B.向下做匀速直线运动

C.向下做匀加速直线运动

D.向下做自由落体运动

[解析] 甲相对于乙的加速度为零.相对于乙的速度向下，故甲相对于乙向下做匀速直线运动，选项B正确.

[答案] B

3.以v=36 km/h的速度沿平直公路行驶的汽车，遇障碍刹车后获得大小为a=4 m/s²的加速度.刹车后3 s内，汽车走过的路程为

A.12 m　　　　　　　　 　　　　　　　　　　　　　　　　　　　 B.12.5 m

C.90 m　　　　　　　　 　　　　　　　　　　　　　　　　　　　 D.126 m

[解析] v=36 km/h=10 m/s，刹车时间为t=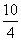 s=2.5 s＜3 s,则汽车在3 s内的位移为s= 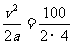m=12.5m.

[答案] B

2.1991年5月11日的《北京晚报》曾报道了这样一则动人的事迹：5月9日下午，一位4岁小男孩从高层塔楼的15层坠下，被同楼的一位青年在楼下接住，幸免于难.设每层楼高度是3 m，这位青年从他所在地方冲到楼下需要的时间是1.3 s，则该青年要接住孩子，至多允许他反应的时间是(g=10 m/s²)

A.3.0 s　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　 B.1.7 s

C.0.4 s　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　 D.1.3 s

[解析] 由自由落体运动知，小孩落地时间为t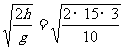＝ s＝3 s，故反应时间为1.7 s.

[答案] B

1.某质点的位移随时间变化的关系式为s=4t+2t²，s与t的单位分别是m与s，则质点的初速度和加速度分别为

A.4 m/s和2 m/s²　　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.0 和4 m/s²

C.4 m/s和4 m/s²　　　　　　　 　　　　　　　　　　　　　　　　 D.4 m/s和0

[答案] C

2.解题方法指导

(1)要养成根据题意画出物体运动示意图的习惯.特别对较复杂的运动，画出草图可使运动过程直观，物理图景清晰，便于分析研究.

(2)要注意分析研究对象的运动过程，搞清整个运动过程按运动性质的转换可分为哪几个运动阶段，各个阶段遵循什么规律，各个阶段间存在什么联系.

(3)由于本章公式较多，且各公式间有相互联系，因此，本章的题目常可一题多解.解题时要思路开阔，联想比较，筛选最简捷的解题方案.解题时除采用常规的公式解析法外，图像法、比例法、极值法、逆向转换法(如将一匀减速直线运动视为反向的匀加速直线运动)等也是本章解题中常用的方法.

●典例剖析

［例1］以速度为10 m/s匀速运动的汽车在第2 s末关闭发动机，以后为匀减速运动，第3 s内平均速度是9 m/s，则汽车加速度是　　 m/s²，汽车在10 s内的位移是　　 　m.

[解析] 第3 s初的速度v₀＝10 m/s，第3.5 s末的瞬时速度v_t=9 m/s (推论(2))

所以汽车的加速度：a=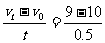 m/s²＝－2 m/s²

“-”表示a的方向与运动方向相反.

汽车关闭发动机后速度减到零所经时间：

t₂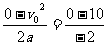＝ s=5 s＜8 s

则关闭发动机后汽车8 s内的位移为：

s₂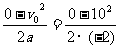＝ m＝25 m

前2 s汽车匀速运动：s₁＝v₀t₁

　　　　　　　　　　 ＝10×2 m＝20 m

汽车10 s内总位移：s=s₁+s₂

　　　　　　　　　 ＝20 m+25 m＝45 m

[说明] (1)求解类似于本题第二个空的问题时，一定要判断清楚所给时间内物体的运动情况，否则乱套公式，得到的多是错误的结论.

(2)本题求s₂时也可用公式s=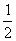at²计算.也就是说：“末速度为零的匀减速运动”可倒过来看作“初速度为零的匀加速运动”.

[设计意图] 通过本例说明对“刹车”类问题，要注意确定“刹车”时间.

［例2］一物体放在光滑水平面上，初速度为零.先对物体施加一向东的恒力F，历时1 s；随即把此力改为向西，大小不变，历时1 s；接着又把此力改为向东，大小不变，历时1 s；如此反复，只改力的方向，共历时1 min.在此1min内

A.物体时而向东运动，时而向西运动，在1 min末静止于初始位置之东

B.物体时而向东运动，时而向西运动，在1 min末静止于初始位置

C.物体时而向东运动，时而向西运动，在1 min末继续向东运动

D.物体一直向东运动，从不向西运动，在1 min末静止于初始位置之东

[解析] 物体初速度为零，在恒力的作用下将做匀变速直线运动.第1 s内向东匀加速，末速度为v，第2 s内力的方向改为向西，由于初速度向东，所以物体向西做匀减速运动，第2 s末时速度减为零.之后物体将重复前2 s内的运动，因此在1 min内的整个过程中，物体的运动方向始终向东，1 min末时的速度为零.所以选项D正确.

本题利用“图象法”求解亦很简单.根据题意，物体的速度图象如图2-2-1所示.

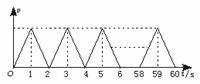
图2-2-1

由图象很容易得出：物体始终沿正方向(东)运动，位移s＞0，1 min末时速度为零.答案为D.

[思考] 如果在奇数秒末物体的速度v_m＝10 m/s，则物体在1 min内的位移多大?

[思考提示] 若物体在奇数秒末的速度为10 m/s，则物体在1 min内的平均速度为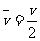 =5 m/s，则物体在1 min内的位移为s=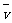t=300 m.

[设计意图] 通过本例说明，当物体的加速度周期变化时，如何判断物体的速度变化及位移，如何总结物体的运动规律.

［例3］跳伞运动员做低空跳伞表演，当飞机离地面224 m时，运动员离开飞机在竖直方向做自由落体运动.运动一段时间后，立即打开降落伞，展伞后运动员以12.5 m/s²的平均加速度匀减速下降.为了运动员的安全，要求运动员落地速度最大不得超过5 m/s.g=10 m/s².求：

(1)运动员展伞时，离地面的高度至少为多少?着地时相当于从多高处自由落下?

(2)运动员在空中的最短时间为多少?

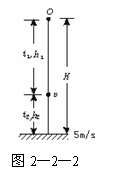[解析] 运动员跳伞表演的过程可分为两个阶段，即降落伞打开前和打开后.由于降落伞的作用，在满足最小高度且安全着地的条件下，可认为v_m=5 m/s的着地速度方向是竖直向下的，因此求解过程中只考虑其竖直方向的运动情况即可.在竖直方向上的运动情况如图2-2-2所示.

(1)由公式v_t²－v₀²＝2as可得

第一阶段：v²＝2gh₁　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

第二阶段：v²－v_m²＝2ah₂　　　　　　　　　　　　　　　　　　　　　　　　　 ②

又：h₁+h₂＝H　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

解①②③式可得展伞时离地面的高度至少为h₂＝99 m.

设以5 m/s速度着地相当于从高h′处自由下落.则

h′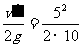＝ m＝1.25 m

(2)由公式s=v₀t+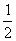at²可得：

第一阶段：h₁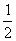＝gt₁²　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

第二阶段：h₂＝vt₂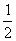－at₂²　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

又：t=t₁+t₂　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

解④⑤⑥式可得运动员在空中的最短时间为t=8.6 s.

[思考] 为什么展伞高度至少为99 m？为什么8.6 s为运动员在空中的最短时间？

[思考提示] 因为展伞高度99 m和在空中的运动时间8.6 s是按最大落地速度5 m/s求得，实际落地速度应为v≤5 m/s，故展伞高度h≥99 m，在空中运动时间t≥8.6 s.

[说明] 简要地画出运动过程示意图，并且在图上标出相对应的过程量和状态量，不仅能使较复杂的物理过程直观化，长期坚持下去，更能较快地提高分析和解决较复杂物理问题的能力.

[设计意图] 通过本例说明，对于这种多过程问题，应注意通过作图等手段，分析清楚各过程的特点及相互联系.然后根据各自的特点列方程求解.

［例4］火车以速度v₁匀速行驶，司机发现前方同轨道上相距s处有另一列火车沿同方向以速度v₂(对地、且v₁＞v₂)做匀速运动.司机立即以加速度a紧急刹车.要使两车不相撞，a应满足什么条件?

[解析] 此题有多种解法.

解法1：两车运动情况如图2-2-3所示，后车刹车后虽做匀减速运动，但在其速度减小至和v₂相等之前，两车的距离仍将逐渐减小；当后车速度减小至小于前车速度，两车距离将逐渐增大.可见，当两车速度相等时，两车距离最近.若后车减速的加速度过小，则会出现后车速度减为和前车速度相等之前即追上前车，发生撞车事故；若后车减速的加速度过大，则会出现后车速度减为和前车速度相等时仍未追上前车，根本不可能发生撞车事故；若后车加速度大小为某值时，恰能使两车在速度相等时后车追上前车，这正是两车恰不相撞的临界状态，此时对应的加速度即为两车不相撞的最小加速度.综上分析可知，两车恰不相撞时应满足下列两方程：

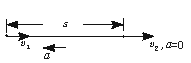
图2-2-3

　 v₁t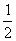－a₀t²＝v₂t+s　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

　 v₁－ɑ₀t＝v₂　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

解之可得：ɑ₀＝.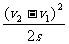

所以当a≥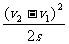时，两车即不会相撞.

解法2：要使两车不相撞，其位移关系应为

　 v₁t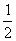－ɑt²≤s+v₂t

即　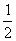　 at²+(v₂－v₁)t+s≥0

对任一时间t,不等式都成立的条件为

　 Δ＝(v₂－v₁)²－2ɑs≤0

由此得a≥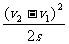

解法3：以前车为参照物，刹车后后车相对前车做初速度v₀＝v₁－v₂，加速度为a的匀减速直线运动.当后车相对前车的速度减为零时，若相对位移s′≤s,则不会相撞.故由

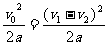　s′＝≤s

得　　 a≥.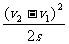

[说明] 解法1注重对运动过程的分析，抓住两车间距离有极值时速度应相等这一关键条件来求解；解法2中由位移关系得到一元二次方程，然后利用根的判别式来确定方程中各系数间的关系，这也是中学物理中常用的数学方法；解法3通过巧妙地选取参照物，使两车运动的关系变得简明.

[设计意图] (1)说明追及、相遇和避碰问题的分析方法；(2)说明如何根据临界条件求解临界问题：(3)说明一个物理问题可有多种分析方法.

※［例5］天文观测表明，几乎所有远处的恒星(或星系)都在以各自的速度背离我们而运动，离我们越远的星体，背离我们运动的速度(称为退行速度)越大；也就是说，宇宙在膨胀，不同星体的退行速度v和它们离我们的距离r成正比，即

v=Hr

式中H为一常量，称为哈勃常数，已由天文观察测定.为解释上述现象，有人提出一种理论，认为宇宙是从一个大爆炸的火球开始形成的，假设大爆炸后各星体即以不同的速度向外匀速运动，并设想我们就位于其中心，则速度越大的星体现在离我们越远，这一结果与上述天文观测一致.

由上述理论和天文观测结果，可估算宇宙年龄T，其计算式为T=　　　 .根据近期观测，哈勃常数H=3×10^－2 m/(s·光年)，其中光年是光在一年中行进的距离，由此估算宇宙的年龄约为　　　 年.

[解析] 由题意可知，可以认为宇宙中的所有星系均从同一点同时向外做匀速直线运动.由于各自的速度不同，所以星系间的距离都在增大.以地球为参照物，所有星系以不同的速度均在匀速远离.则由s=vt可得r=vT

所以，宇宙年龄：T=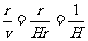

若哈勃常数H=3×10^－2 m/(s·光年)

则T=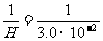×2.0×10⁸年=10¹⁰年

[说明] 本题是理论联系实际的题目，把宇宙现象转化为物理模型是解决本题的关键.该类题目的共同特点是：背景资料较长，信息较多.在审题过程中要能抓住主要矛盾，要学会透过现象看本质，要善于将实际问题抽象为物理问题.

[设计意图] 近几年高考加强了物理跟社会、生产、生活及科技的联系，对于这类题目又是学生的薄弱点.通过本例使学生明确，对于这类跟生产生活实际及科技联系的题目，建立物理模型是解这类题目的关键.同时使学生认识到这类题目看上去很难、很高深，其实物理模型可能很简单.

●反馈练习

★夯实基础

1.追及和相遇问题

在两物体同直线上的追及、相遇或避免碰撞问题中关键的条件是：两物体能否同时到达空间某位置.因此应分别对两物体研究，列出位移方程，然后利用时间关系、速度关系、位移关系而解出.

(1)追及

追和被追的两者的速度相等常是能追上、追不上、二者距离有极值的临界条件.

如匀减速运动的物体追同向的匀速运动的物体时，若二者速度相等了，追者位移仍小于被追者位移，则永远追不上，此时二者间有最小距离.若二者位移相等(追上)了，追者速度等于被追者的速度，则恰能追上，也是二者避免碰撞的临界条件；若二者位移相等时追者速度仍大于被追者的速度，则被追者还有一次追上追者的机会，其间速度相等时二者的距离有一个较大值.

再如初速为零的匀加速运动的物体追同向匀速运动的物体时，当二者速度相等时二者有最大距离，位移相等即追上.

(2)相遇

同向运动的两物体追及即相遇，分析同(1).

相向运动的物体，当各自发生的位移的绝对值的和等于开始时两物体间的距离时即相遇.

5.自由落体运动是初速度为0、加速度为g的匀加速直线运动，初速度为零的匀加速运动的所有规律和比例关系均适用于自由落体运动.

●疑难辨析