
2. 设集合A和集合B都是自然数集合N,映射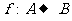 把集合A中的元素
把集合A中的元素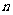 映射到集合B中的元素
映射到集合B中的元素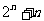 ,则在映射
,则在映射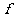 下,象20的原象是 (
)
下,象20的原象是 (
)
(A)2 (B)3 (C)4 (D)5
1.若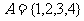 ,
,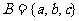 ,则
,则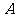 到
到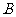 的映射有
个,
的映射有
个,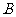 到
到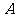 的映射有 个;若
的映射有 个;若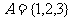 ,
,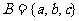 , 则
, 则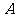 到
到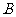 的一一映射有 个。
的一一映射有 个。
5.函数值域的求法:①配方法(二次或四次);②判别式法;③反函数法(反解法);④换元法(代数换元法);⑤不等式法;⑥单调函数法.
注:⑴求函数值域是函数中常见问题,在初等数学范围内,直接法的途径有单调性,基本不等式及几何意义,间接法的途径为函数与方程的思想,表现为△法,反函数法等,在高等数学范围内,用导数法求某些函数最值(极值)更加方便.
⑵常用函数的值域,这是求其他复杂函数值域的基础。
①
函数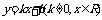 的值域为R;
的值域为R;
②
二次函数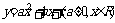
当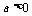 时值域是
时值域是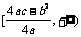 ,当
,当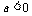 时值域是
时值域是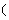

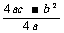 ];
];
③
反比例函数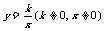 的值域为
的值域为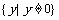 ;
;
④
指数函数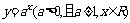 的值域为
的值域为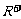 ;
;
⑤
对数函数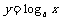
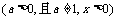 的值域为R;
的值域为R;
⑥
函数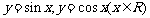 的值域为[-1,1];
的值域为[-1,1];
⑦
函数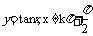 ,
,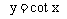
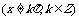 的值域为R;
的值域为R;
4.函数定义域的求法:列出使函数有意义的自变量的不等关系式,求解即可求得函数的定义域.常涉及到的依据为:①分母不为0;②偶次根式中被开方数不小于0;③对数的真数大于0,底数大于零且不等于1;④零指数幂的底数不等于零;⑤实际问题要考虑实际意义等.
注:求函数定义域是通过解关于自变量的不等式(组)来实现的。函数定义域是研究函数性质的基础和前提。函数对应法则通常表现为表格,解析式和图象。
3.函数的三要素:定义域,值域,对应法则. 从逻辑上讲,定义域,对应法则决定了值域,是两个最基本的因素。
2.函数定义:函数就是定义在非空数集A,B上的映射,此时称数集A为定义域,象集C={f(x)|x∈A}为值域。
1.映射:设非空数集A,B,若对集合A中任一元素a,在集合B中有唯一元素b与之对应,则称从A到B的对应为映射,记为f:A→B,f表示对应法则,b=f(a)。若A中不同元素的象也不同,且B中每一个元素都有原象与之对应,则称从A到B的映射为一一映射。
马鞍山市第二中学2009-2010学年度
12.⑴ ⑵
⑶ ⑷
⑸ ⑹
⑺ ⑻
⑼ ⑽
⑾ ⑿
⒀
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com