
6、如图所示,一些商场安装了智能化的自动扶梯。为了节约能源,在没有乘客乘行时,自动扶梯以较小的速度匀速运行,当有乘客乘行时自动扶梯经过先加速再匀速两个阶段运行。则电梯在运送乘客的过程中:
 A.乘客始终受摩擦力作用
A.乘客始终受摩擦力作用
B.乘客经历先超重再失重
C.乘客对扶梯的作用力先指向右下方,再竖直向下
D.扶梯对乘客的作用力始终竖直向上
5、下列说法中正确的是:
A.在α粒子散射实验中,使少数α粒子产生大角度偏转的力是原子核对粒子的库仑斥力
B.氢原子在辐射出一个光子后,核外电子的动能增大
C.已知氦原子的质量m1、电子质量m2、质子质量m3、中子质量m4,则质子和中子在结合成氦核时的质量亏损为(2 m4+2 m3-m1)
D.爱因斯坦狭义相对论的基本结论之一是运动物体长度会收缩,即l =l0 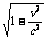 ,它是因时空条件不同而引起的观测效应
,它是因时空条件不同而引起的观测效应
4、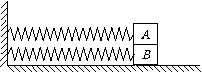 如图所示,质量相等的物块A、B叠放在光滑水平面上,两轻质弹簧的一端固定在竖直墙壁上,另一端分别与A、B相连接,两弹簧的原长相同,与A相连的弹簧的劲度系数小于与B相连的弹簧的劲度系数。开始时A、B处于静止状态。现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置(A、B无相对滑动,弹簧处于弹性限度内),撤去这个力后:
如图所示,质量相等的物块A、B叠放在光滑水平面上,两轻质弹簧的一端固定在竖直墙壁上,另一端分别与A、B相连接,两弹簧的原长相同,与A相连的弹簧的劲度系数小于与B相连的弹簧的劲度系数。开始时A、B处于静止状态。现对物块B施加一水平向右的拉力,使A、B一起向右移动到某一位置(A、B无相对滑动,弹簧处于弹性限度内),撤去这个力后:
A.A受到的合力总等于弹簧对B的弹力
B.A受到的合力总大于弹簧对B的弹力
C.A受到的摩擦力始终与弹簧对它的弹力方向相同
D.A受到的摩擦力与弹簧对它的弹力方向有时相同,有时相反
3、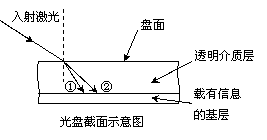 在信息技术迅猛发展的今天,光盘是存
储信息的一种重要媒介.光盘上的信息通常是通过激光束来读取的.若激光束不是垂直投射到盘面上,则光线在通过透明介质层时会发生偏折而改变行进的方向,如图所示.下列说法中不正确的是:
在信息技术迅猛发展的今天,光盘是存
储信息的一种重要媒介.光盘上的信息通常是通过激光束来读取的.若激光束不是垂直投射到盘面上,则光线在通过透明介质层时会发生偏折而改变行进的方向,如图所示.下列说法中不正确的是:
A.图中光束①是红光,光束②是蓝光
B.在光盘的透明介质层中,光束①比光束②传播速度更快
C.若光束①、②先后通过同一单缝衍射装置,光束①的中央亮纹比光束②的窄
D.若光束①、②先后通过同一双缝干涉装置,光束①的条纹宽度比光束②的宽
2、足球运动员在距球门正前方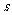 处的罚球点,准确地从球门正中央横梁下边缘踢进一球.横梁下边缘离地面的高度为
处的罚球点,准确地从球门正中央横梁下边缘踢进一球.横梁下边缘离地面的高度为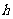 ,足球质量为
,足球质量为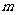 ,空气阻力忽略不计.运动员至少要对足球做的功为
,空气阻力忽略不计.运动员至少要对足球做的功为 .
.
下面给出功 的四个表达式中只有一个是合理的,你可能不会求解
的四个表达式中只有一个是合理的,你可能不会求解 ,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断,
,但是你可以通过一定的物理分析,对下列表达式的合理性做出判断.根据你的判断, 的合理表达式应为:
的合理表达式应为:
A.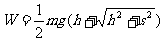
B.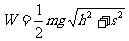
C.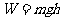
D.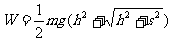
孝感三中---严防转载
1、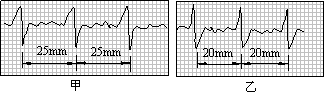
 心电图仪(如右图所示)通过一系列的传感手段,可将与人心跳对应的生物电流情况记录在匀速运动的坐标纸上.医生通过心电图,可以了解到被检者心跳的情况,例如,测量相邻两波峰的时间间隔,便可计算出1 min内心脏跳动的次数(即心率).同一台心电图仪正常工作时测得待检者甲、乙的心电图分别如图甲、乙所示.若医生测量时记下被检者甲的心率为60次/ min,则可推知乙的心率和这台心电图仪输出坐标纸的走纸速度大小分别为
心电图仪(如右图所示)通过一系列的传感手段,可将与人心跳对应的生物电流情况记录在匀速运动的坐标纸上.医生通过心电图,可以了解到被检者心跳的情况,例如,测量相邻两波峰的时间间隔,便可计算出1 min内心脏跳动的次数(即心率).同一台心电图仪正常工作时测得待检者甲、乙的心电图分别如图甲、乙所示.若医生测量时记下被检者甲的心率为60次/ min,则可推知乙的心率和这台心电图仪输出坐标纸的走纸速度大小分别为
A.48次/ min,25 mm/s B.75次/ min,25 mm/s
C.75次/ min,45 mm/s D.48次/ min,36 mm/s
4. 4 5.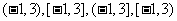 .6.
.6. 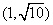 . 7. 1 . 8.
. 7. 1 . 8.
 .9.
.9. 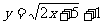 . 10是
. 10是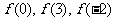 . 11.__(1,3]____12.是
. 11.__(1,3]____12.是 . 13.是___①_____.
14. 1
.
. 13.是___①_____.
14. 1
.
5解:由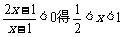 ,设集合
,设集合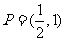
由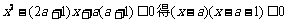
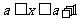 ,设集合
,设集合
p是q的充分不必要条件得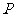 是
是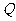 的真子集,故
的真子集,故 得
得
16解:(1)由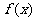 =
=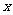 +
+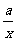 得
得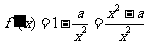 ,
2分
,
2分
当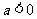 时,
时,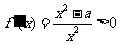 恒成立,所以函数
恒成立,所以函数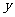 =
=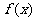 在
在 上为增函数; 4分
上为增函数; 4分
当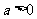 时,令
时,令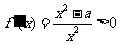 ,解得
,解得 ,
,
令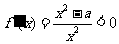 ,解得
,解得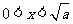 ,
,
所以函数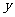 =
=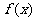 在
在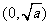 上为减函数;在
上为减函数;在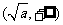 上为增函数。 7分
上为增函数。 7分
(2)由(1)可知当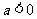 时,函数
时,函数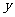 =
=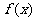 在
在 上为增函数,
上为增函数,
此时函数的值域为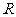 ,不合题意;
9分
,不合题意;
9分
当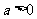 时,函数
时,函数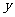 =
=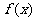 在
在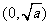 上为减函数;
上为减函数;
在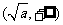 上为增函数,此时函数的值域为
上为增函数,此时函数的值域为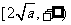 ,即
,即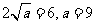 。
。
综上,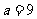 。
14分
。
14分
17解:方法一:由定义在R上的函数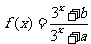 是奇函数得对一切
是奇函数得对一切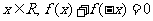 恒成立
恒成立
即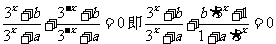 ,
,
整理得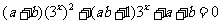 对任意
对任意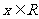 恒成立,
恒成立,
故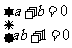 ,解得
,解得 ,
,
又因为函数的定义域为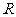 ,故
,故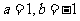 。
5分
。
5分
方法二:由题意可知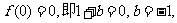 此时
此时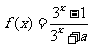 ,
,
又由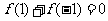 得
得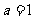 ,此时
,此时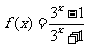 ,经检验满足
,经检验满足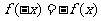 符合题意。
符合题意。
(不检验扣1分) 5分
(2)由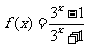 得
得
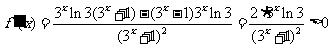 恒成立,
恒成立,
故函数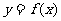 在R上为增函数。
10分
在R上为增函数。
10分
(3) 函数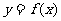 为奇函数且在R上为增函数
为奇函数且在R上为增函数
由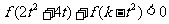 得
得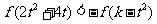
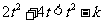 12分
12分
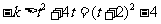 对一切
对一切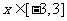 恒成立
恒成立
所以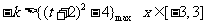
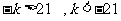 15分
15分
注:若选择用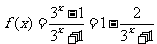 在R上为增函数,此时要用定义给出证明。
在R上为增函数,此时要用定义给出证明。
18解:(1)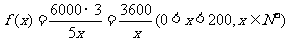 ,
2分
,
2分
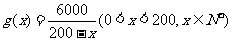 。
4分
。
4分
(2)令
故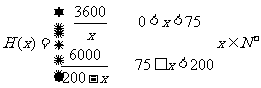 9分
9分
(3)即求函数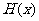 的最小值。当
的最小值。当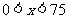 时,
时,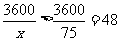 ,当
,当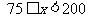 时,
时,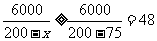 ,故当
,故当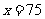 时
时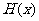 的最小值为
的最小值为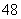 。
。
综上,为了在最短时间内完成工作,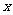 应取
应取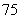 。
15分
。
15分
19 解(1)当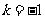 时,
时,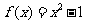 ,又
,又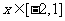 ,故
,故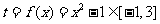
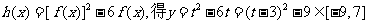 ,
,
也即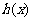 的最大值为7.此时
的最大值为7.此时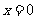 。
7分
。
7分
(2)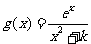 ,
,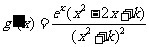 ,因为
,因为 在区间(2,3)上不单调,故
在区间(2,3)上不单调,故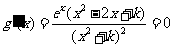 在区间(2,3)上有根,且不能有两个相等的根。
在区间(2,3)上有根,且不能有两个相等的根。
令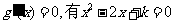 则
则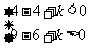 ,解得
,解得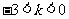 。
16分
。
16分
20解.(1) 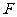
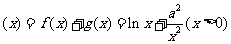
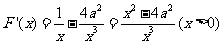
 由
由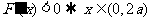 。
。
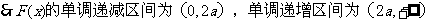 4分
4分
(2)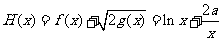 ,
,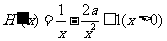 ,则
,则
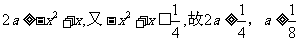 ,
,
所以实数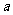 的最小值为
的最小值为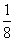 。
10分
。
10分
(3)若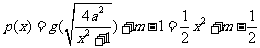 的图象与
的图象与
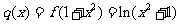 的图象恰有四个不同交点,
的图象恰有四个不同交点,
即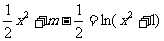 有四个不同的根,亦即
有四个不同的根,亦即
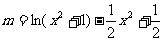 有四个不同的根。
有四个不同的根。
令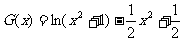 ,
,
则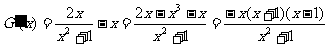 。
。
当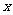 变化时
变化时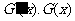 的变化情况如下表:
的变化情况如下表:
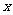 |
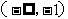 |
(-1,0) |
(0,1) |
(1, ) ) |
 的符号 的符号 |
+ |
- |
+ |
- |
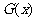 的单调性 的单调性 |
↗ |
↘ |
↗ |
↘ |
由表格知: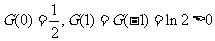 。
。
又因为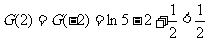 可知,当
可知,当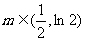 时,
时,
方程
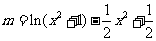 有四个不同的解.
有四个不同的解.

 16分
16分
1.是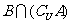 或
或 或
或 等. 2.为
等. 2.为 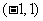 . 3{1,2,3,6}___.
. 3{1,2,3,6}___.
15(本题满分14分)设命题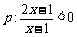 ,命题
,命题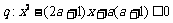 ,若p是q的充分不必要条件,求实数
,若p是q的充分不必要条件,求实数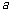 的取值范围.
的取值范围.
16(本题满分14分) 已知函数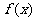 =
=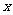 +
+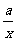 (x>0), a为常数,且
(x>0), a为常数,且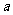
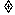 0.
0.
(1)研究函数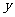 =
=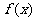 的单调性,并说明理由;
的单调性,并说明理由;
(2)如果函数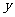 =
=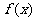 的值域为
的值域为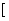 6,+∞
6,+∞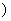 ,求
,求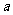 的值.
的值.
17(本题满分15分)已知定义域为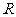 的函数
的函数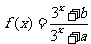 是奇函数.
是奇函数.
(1)求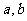 的值;
的值;
(2)讨论函数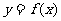 的单调性;
的单调性;
(3)若对任意的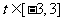 ,不等式
,不等式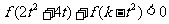 恒成立,求实数
恒成立,求实数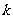 的取值范围.
的取值范围.
18(本题满分15分)某车间有200名工人,要完成6000件产品的生产任务,每件产品由3个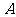 型
零件和1个
型
零件和1个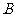 型零件配套组成.每个工人每小时能加工5个
型零件配套组成.每个工人每小时能加工5个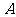 型零件或者1个
型零件或者1个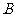 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工
型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一种型号的零件.设加工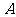 型零件的工人人数为
型零件的工人人数为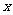 名(
名(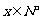 ).
).
(1)设完成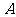 型零件加工所需时间为
型零件加工所需时间为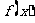 小时,完成B型零件加工所需时间为
小时,完成B型零件加工所需时间为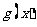 小时,写出
小时,写出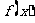 ,
,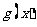 的解析式;
的解析式;
(2)当A、B两种零件全部加工完成,就算完成工作.全部完成工作所需时间为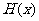 小时,写出
小时,写出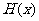 的解析式;
的解析式;
(3)为了在最短时间内完成工作,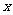 应取何值?
应取何值?
19(本题满分16分)已知函数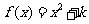
(1)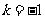 时,设,求
时,设,求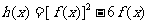 ,
,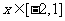 的最大值.
的最大值.
(2)若函数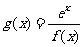 ,且
,且 在区间(2,3)上不单调,求实数k的取值范围.
在区间(2,3)上不单调,求实数k的取值范围.
20(本题满分16分)已知函数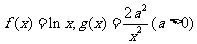 ,设
,设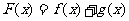 。
。
(1)求F(x)的单调区间;
(2)若以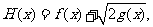 图象上任意一点
图象上任意一点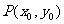 为切点的切线的斜率
为切点的切线的斜率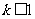 恒成立,求实数
恒成立,求实数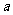 的最小值;
的最小值;
(3)是否存在实数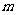 ,使得函数
,使得函数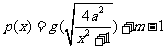 的图象与
的图象与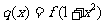 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出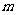 的取值范围,若不存在,说明理由。
的取值范围,若不存在,说明理由。
南通市2010届高三数学十校联考调研检测(理科)
14.对于在区间[a,b]上有意义的两个函数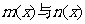 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有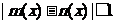 ,则称
,则称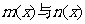 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数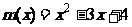 与
与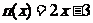 在区间[a,b]上是“密切函数”,则
在区间[a,b]上是“密切函数”,则 的最大值为 ▲ .
的最大值为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com