
21.对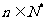 ,不等式
,不等式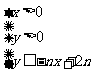 所表示的平面区域为
所表示的平面区域为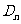 ,把
,把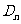 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
(1) 求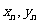
(2) 数列 满足
满足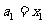 且
且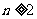 时,
时,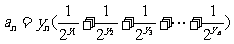 ,求数列
,求数列 的前n项和
的前n项和 .
.
(3) 设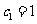 ,当
,当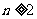 时,
时,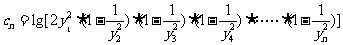 ,且数列
,且数列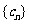 的前n项和
的前n项和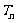 ,求
,求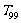 .
.
20.(本小题满分13分)甲方是一农场,乙方是一工厂. 由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润x(元)与年产量t(吨)满足函数关系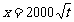 。若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格)。[七彩教育网独家]
。若乙方每生产一吨产品必须赔付甲方s元(以下称s为赔付价格)。[七彩教育网独家]
(1)将乙方的年利润w(元)表示为年产量t(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙方生产影响的经济损失金额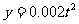 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格s是多少?
19.已知F1、F2是椭圆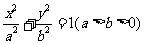 的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足
的左、右焦点,A是椭圆上位于第一象限内的一点,点B也在椭圆上,且满足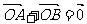 (
(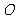 是坐标原点),
是坐标原点), ,若椭圆的离心率等于
,若椭圆的离心率等于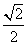 .
.
(1)求直线AB的方程;
(2)若三角形ABF2的面积等于4 ,求椭圆的方程;
,求椭圆的方程;
(3)在(2)的条件下,椭圆上是否存在点M,使得三角形MAB的面积等于8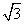 .
.
18.已知函数[七彩教育网独家]f(x)= 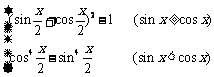
(1)画出f(x)在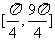 上的图象,并写出x∈
上的图象,并写出x∈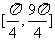 上的单调区间;
上的单调区间;
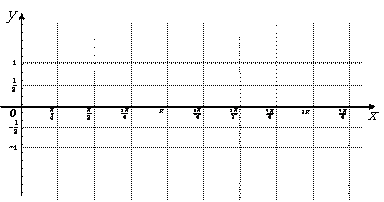 (2)若x∈R,判断f(x)是否为周期函数。如果是,求出最小正周期。
(2)若x∈R,判断f(x)是否为周期函数。如果是,求出最小正周期。
17. 已知某单位有50名职工,现要从中抽取
已知某单位有50名职工,现要从中抽取
10名职工,将全体职工随机按1~50编号,并
号顺序平均分成10组,按各组内抽按编取的
编号依次增加5进行系统抽样。
(1)若第5组抽出的号码为22,写出
所有被抽出职工的号码;
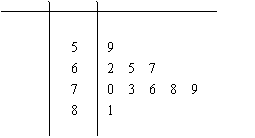
(2)分别统计这10名职工的体重(单
位:公斤),获得体重数据的茎叶图如图所
示,求该样本的方差;
(3)在(2)的条件下,从这10名职工中随机抽取两名体重不轻于73公斤( 73公斤)的职工,求被抽取到两名职工体重之和大于等于154公斤的概率。
73公斤)的职工,求被抽取到两名职工体重之和大于等于154公斤的概率。
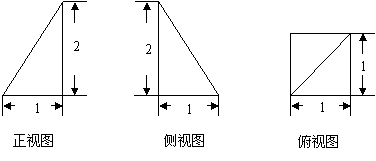
16.已知一个四棱锥P-ABCD的三视图(正视图与侧视图为直角三角形,俯视图是带有一条对角形的正方形)如下,E是侧棱PC上的动点。
(1)求四棱锥P-ABCD的体积;
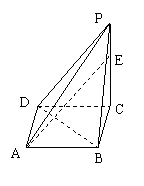 (2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
(2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
15.设n阶方阵
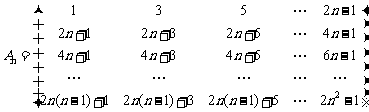
任取A n中的一个元素,记为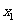 ;划去
;划去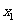 所在行与列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取A n-1中一个元素,记为
所在行与列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取A n-1中一个元素,记为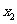 ,划去
,划去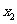 所在行与列,……将最后剩下的一个元素记为
所在行与列,……将最后剩下的一个元素记为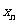 ,记
,记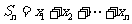 ,
,
若n=3时,则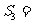 , 若n=k时,则
, 若n=k时,则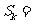 。
。
{007}
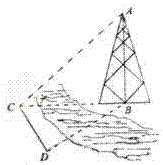
14.如图,测量河对岸的塔高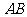 时,可以选与塔底
时,可以选与塔底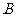 在
在
同一水平面内的两个测点 与
与 .测得∠BCD=15°,
.测得∠BCD=15°,
∠BDC=30°,CD=30米,并在点 测得塔顶
测得塔顶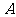
的仰角为60°, 则塔高AB= 米。
13. 已知
已知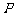 是边长为2的正
是边长为2的正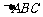 边
边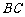 上的动点,
上的动点,
则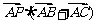 =
=
12.用辗转相除法求得459和357的最大公约数是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com