22．(本小题满分12分)

设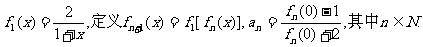

(Ⅰ)求数列{a_n}的通项公式；

(Ⅱ)若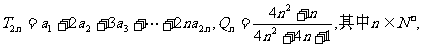试比较9T_2n与Q_n的大小，并说明理由.

21．(本小题满分12分)

已知点H(-3，0)，点P在y轴上，点Q在x轴的正半轴上，点M在直线PQ上，且满足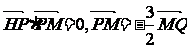

(Ⅰ)当点P在y轴上移动时，求点M的轨迹C；

(Ⅱ)过点T(-1，0)作直线l与轨迹C交于A、B两点，若在x轴上存在一点E(x₀,0)，使得△ABE是等边三角形，求x₀的值.

20．(本小题满分12分)

苏南某城市在发展过程中，交通状况逐渐受到大家更多的关注，据有关统计数据显示，从上午6点到中午12点，车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间关系可近似地用如下函数给出：

　 求从上午6点到中午12点，通过该路段用时最多的时刻.

已知每盘比赛双方胜出的概率均为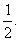

(Ⅰ)根据比赛规则，高三(1)班代表队共可排出多少种不同的出场阵容？

(Ⅱ)高三(1)班代表队连胜两盘的概率是多少？

(Ⅲ)高三(1)班代表队至少胜一盘的概率为多少？

19．(本小题满分12分)

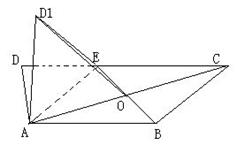
如图，在梯形ABCD中，AB∥CD，∠ADC=90°3AD=DC=3，AB=2，E是DC上一点，满足DE=1，连接AE，将△DAE沿AE折起到△D₁AE的位置，使得∠D₁AB=60°，设AC与BE的交点O.

(Ⅰ)试用基向量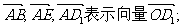

(Ⅱ)求异面直线OD₁与AE所成的角；

(Ⅲ)判断平面D₁AE与平面ABCE是否垂直？并说明理由.

18．(本小题满分12分)

17．(本小题满分12分)

在△ABC中，角A、B、C的对边分别为a、b、c且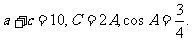

　　 求：(Ⅰ)(Ⅱ)b的值.

16．如果函数f(x)的定义域为R，对于

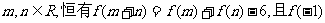是不大于5的正整数，当x>－1时，f(x)>0.那么具有这种性质的函数f(x)=　　　　　 　(注：填上你认为正确的一个函数即可，不必考虑所有可能的情形).

15．△ABC的内角A满足tanA－sinA<0,且sinA+cosA>0，则角A的取值范围是____ 　.

14．若a、b表示直线α、β、表示平面，给出三个命题：

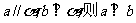　 ① 若; ② 若;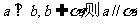

③ 若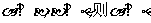.其中正确的命题是 　　　　　　　　　(将你认为正确命题的序号都填上).

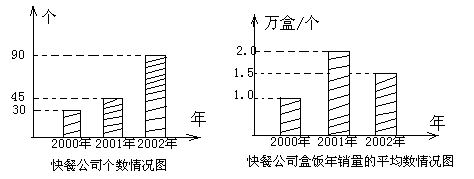
13．一个高中研究性学习小组对本地区2000年至2002年快餐公司发展情况进行了调查，制成了该地区快餐公司个数情况的条形图和快餐公司盒饭年销售量的平均数情况条形图(如图)，根据图中提供的信息可以得出这三年中该地区每年平均销售盒饭　　 　_____________万盒.