6、解答三角高考题的策略。

(1)发现差异：观察角、函数运算间的差异，即进行所谓的“差异分析”。

(2)寻找联系：运用相关公式，找出差异之间的内在联系。

(3)合理转化：选择恰当的公式，促使差异的转化。

5、三角函数的图象

(1)画三角函数的图象应先求函数的周期，然后用五点法画出函数一个周期的图象．

(2)函数y=sinx，y=cosx，y=tanx，y=cotx　 图象的对称中心分别为

∈Z)的直线．

4、三角函数的值域

(1)由|sinx|≤1、|cosx|≤1得函数y=cscx、y=secx的值域是|cscx|≥1、|secx|≥1．

(2)复合三角函数的值域问题较复杂，除了代数求值域的方法都可以适用外，还要注意三角函数本身的特点，特别是经常需要先进行三角变换再求值域．

常用的一些函数的值域要熟记．

③y=tanx+cotx∈(-∞，-2]∪[2，+∞)．

3、三角形中的三角变换

三角形中的三角变换，除了应用上述公式和上述变换方法外，还要注意三角形自身的特点．

正弦定理　 (R为外接圆半径)．

余弦定理　 c² = a²+b²－2bccosC，b² = a²+c²－2accosB，a² = b²+c²－2bccosA．

它们的变形形式有：a = 2R sinA，，．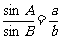

(4)面积公式：

．

解斜三角形的常规思维方法是：

(1)已知两角和一边(如A、B、C)，由A+B+C = π求C，由正弦定理求a、b．

(2)已知两边和夹角(如a、b、c)，应用余弦定理求c边；再应用正弦定理先求较短边所对的角，然后利用A+B+C = π，求另一角．

(3)已知两边和其中一边的对角(如a、b、A)，应用正弦定理求B，由A+B+C = π求C，再由正弦定理或余弦定理求c边，要注意解可能有多种情况．

(4)已知三边a、b、c，应余弦定理求A、B，再由A+B+C = π，求角C．

2、和差化积、积化和差公式，这两组公式现在不要求记忆，但要会使用．

(1)要明确，这两组公式是解决正、余弦的加、减、乘的运算关系式．

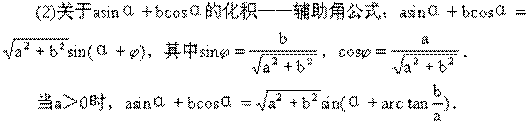
(3)对下列关系式要熟记：

1、余弦的二倍角公式的变形--升幂公式、降幂公式必须熟练掌握．要明确，降幂法是三角变换中非常重要的变形方法．

20．(本小题满分13分)

　　　 已知数列

　　　 (1)求、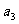的值；

　　　 (2)证明当

山西省太原十中2010届高三下学期第二次模拟考试数学试题

19．(本小题满分14分)

　　　 已知O为坐标原点，点E、F的坐标分别为(－1，0)和(1，0)，点P满足

　　　 (1)求动点P的轨迹C的方程；

　　　 (2)过E点做直线与C相交于M、N两点，且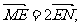求直线MN的方程.

18．(本小题满分13分)

　　　 已知函数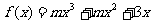在R上是增函数，求实数m的取值范围.

17．(本小题满分14分)

　　　 已知直三棱柱ABC-A₁B₁C₁中，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA₁=a，D、E、F分别为B₁A、C₁C、BC的中点.

　　　 (1)求证：DF//平面ABC；

　　　 (2)求二面角B₁-AF-B的大小(用反三角函数表示)；

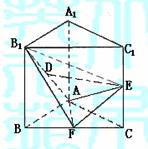　 　　　 (3)求三棱锥F-B₁AE的体积.