
9.八个国家中,沙漠面积广布的两个国家是
A.喀麦隆、苏丹 B.赞比亚、南非 C.苏丹、纳米比亚 D.纳米比亚、南非
下图为我国某区域地图,读图完成6-8题。

6.图示区域棉花种植区主要分布在
A.山区 B.城市周边地区
C.塔里木河下游 D.盆地中部
7.图示区域城乡聚落规划时优先考虑的因素是
A.丰富的水源 B.便捷的交通 C.适宜的气候 D.平坦的地形
8.乌鲁木齐的某地理要素等值线由里向外逐渐减小,该等值线最不可能代表的是
A.降水量 B.土地租金 C.气温分布 D.人口自然增长率
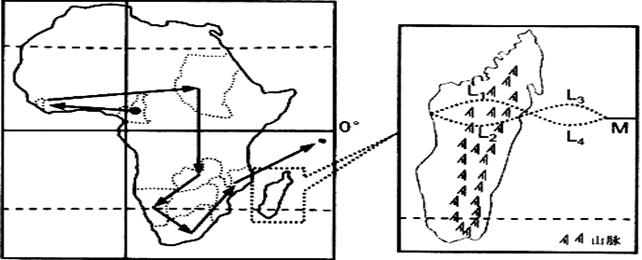
下图是国家主席胡锦涛先后对喀麦隆、利比里亚、苏丹、赞比亚、纳米比亚、南非、莫桑比克、塞舌尔8个国家访问线路示意图。
读我国四座城市气温年较差和年降水量坐标图,读图完成4-5题。

4.一般年份,影响这四座城市所在区域农业发展的不利因素或灾害分别是
A.a热量,b光照,c伏旱,d洪涝 B.a水分,b春旱,c伏旱,d洪涝
C.a热量,b春旱,c伏旱,d台风 D.a水分,b盐碱,c光照,d台风
5.依据四地所处的温度带判断,其适宜种植的农作物分别是
A.a棉花,b冬小麦,c油菜,d甘蔗 B.a甜菜,b春小麦,c水稻,d水稻
C.a亚麻,b棉花,c油菜,d甘蔗 D.a春小麦,b冬小麦,c橡胶,d水稻
下图中图甲为晨昏线与北半球纬线圈相切点P的纬度年变化示意图,图乙为太阳直射点Q位置周年变化图,读图完成1-3题。

图甲 图乙
1、图中①~⑤代表一个回归年中P点五个的纬度位置,图乙中a~e代表一个回归年中Q点的五个纬度位置,下列关于PQ两点位置相关性的说法中,正确的是
A.P点位于①时,Q可能在a处 B.P点位于③时,Q可能在b处
C.P点位于④时,Q一定在c处 D.P点位于⑤时,Q一定在d处
2、下列关于P点的纬度变化与现象的选项中,正确的是
A.P点从①到②时,上海的昼长逐日变长 B.P点从③到④时,上海的昼长逐日变短
C.P点位于②④时,上海白昼最长 D.P点位于⑤时,上海昼夜平分
3、下列关于Q点的纬度变化与现象的选项中,错误的是
A.Q点从a到c时,新加坡的正午太阳高度逐日减小
B.Q点从b到d时,地中海沿岸温和多雨
C.Q点位于c时,从大西洋驶入地中海的货轮顺风顺水
D.Q点位于e时,北印度洋环流呈顺时针方向流动
本部分共35题,每题4分,共140分。在每题给出的四个选项中,只有一项是最符合题目要求的。
22. (本小题满分12分)(理科)已知函数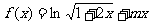 .
.
(I)若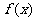 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数 的取值范围;
的取值范围;
(II)当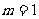 ,且1≥
,且1≥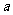 >
>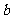 ≥0时,证明:
≥0时,证明: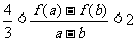 .
.
答案:(I)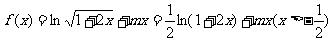 ,
,
∴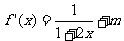 ……2分
……2分
对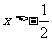 ,
,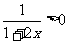 ,故不存在实数m,
,故不存在实数m,
使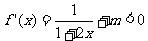 对
对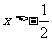 恒成立,……4分
恒成立,……4分
由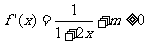 对
对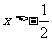 恒成立得,
恒成立得,
 ≥
≥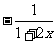 对
对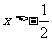 恒成立
恒成立
而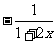 <0,故m≥0
<0,故m≥0
经检验,当m≥0时,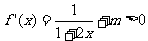 对
对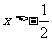 恒成立
恒成立
∴当m≥0时,f (x)为定义域上的单调递增函数.…… 6分
(II)当m = 1时,令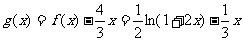
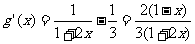 ,
,
在[0,1]上总有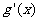 ≥0,
≥0,
即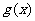 在[0,1]上递增
在[0,1]上递增
∴当1≥a > b≥0时,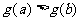 ,
,
即 ……9分
……9分
令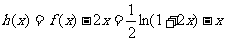 ,由(2)知它在[0,1]上递减,
,由(2)知它在[0,1]上递减,
∴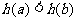
即
综上所述,当m = 1,且1≥a > b≥0时,
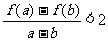 . ……12分
. ……12分
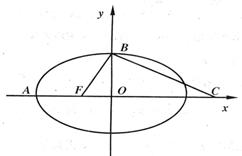 (文科)如图,F是椭圆
(文科)如图,F是椭圆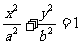 (
(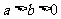 )的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为
)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为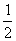 .点C在x轴上,BC⊥BF,B,C,F三点确定的圆M的半径为2.
.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M的半径为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点A的直线l与圆M交于P、Q两点,且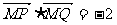 求直线l的方程.
求直线l的方程.
答案:(Ⅰ)F(-c,0),∵椭圆的离心率为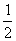 ,
,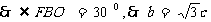 ,
,
∴ B(0,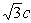 ),C(3c,0)
),C(3c,0)
∴ 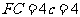 ,解得
,解得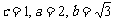
∴所求的椭圆方程为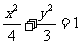 ……………………………………6分
……………………………………6分
(II) 点A的坐标为(-2,0),圆M的方程为(x-1)2+y2=4,
过点A斜率不存在的直线与圆不相交,设直线l2的方程为y=k(x+2),…………………………………7分
∵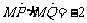 ,又
,又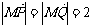 ,∴cos<MP,MQ>=
,∴cos<MP,MQ>=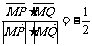 ……………9分
……………9分
∴∠PMQ=120°,圆心M到直线l2的距离d=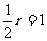 ,
,
所以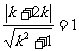 ,∴k=
,∴k=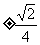 .
.
所求直线的方程为x+2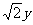 +2=0或X-2
+2=0或X-2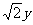 +2=0.……………………………12分
+2=0.……………………………12分
21. (本小题满分12分) (理科)长度为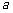 (
( )的线段
)的线段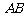 的两个端点
的两个端点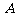 、
、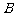 分别在
分别在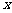 轴和
轴和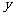 轴上滑动,点
轴上滑动,点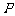 在线段
在线段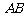 上,且
上,且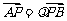 (
( 为常数且
为常数且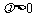 ).
).
(I)求点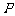 的轨迹方程
的轨迹方程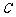 ,并说明轨迹类型;
,并说明轨迹类型;
(II)当 =2时,已知直线
=2时,已知直线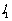 与原点O的距离为
与原点O的距离为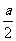 ,且直线
,且直线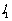 与轨迹
与轨迹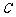 有公共点,求直线
有公共点,求直线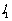 的斜率
的斜率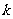 的取值范围.
的取值范围.
答案:(I)设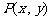 、
、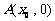 、
、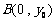 ,则
,则
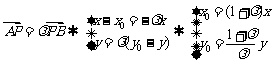 ,由此及
,由此及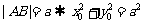 ,得
,得
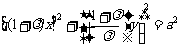 ,即
,即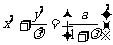 . (*) ……
3分
. (*) ……
3分
①当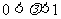 时,方程(*)的轨迹是焦点为
时,方程(*)的轨迹是焦点为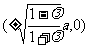 ,长轴长为
,长轴长为 的椭圆;
的椭圆;
②当 时,方程(*)的轨迹是焦点为
时,方程(*)的轨迹是焦点为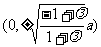 ,长轴长为
,长轴长为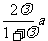 的椭圆;
的椭圆;
③当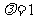 时,方程(*)的轨迹是焦点为以O点为圆心,
时,方程(*)的轨迹是焦点为以O点为圆心,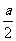 为半径的圆.…… 6分
为半径的圆.…… 6分
(II)设直线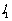 的方程:
的方程: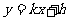 ,据题意有
,据题意有
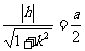 ,即
,即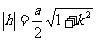 . ……9分
. ……9分
由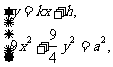 得
得
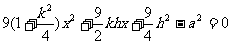 .
.
因为直线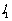 与椭圆
与椭圆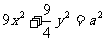 有公共点,所以
有公共点,所以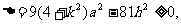
又把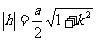 代入上式,得
代入上式,得 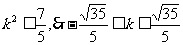 . ……12分
. ……12分
(文科)已知函数
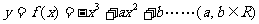 .
.
(Ⅰ) 当 时,若
时,若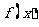 满足:
满足: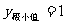 ,
,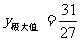 ,试求
,试求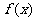 的解析式;
的解析式;
(Ⅱ)若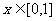 时,
时,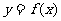 图像上的任意一点处的切线斜率k满足:
图像上的任意一点处的切线斜率k满足: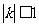 ,求
,求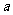 的取值范围.
的取值范围.
答案:(Ⅰ)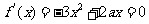 得
得 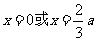 . ……2分
. ……2分
 时,x变化时
时,x变化时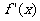 ,
,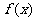 变化如下表:
变化如下表:
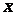 |
 |
0 |
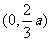 |
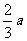 |
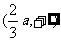 |
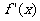 |
- |
0 |
+ |
0 |
- |
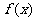 |
  |
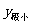 |
   |
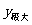 |
  |
所以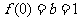 ,
,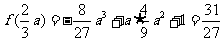 , ……4分
, ……4分
即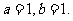
故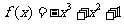 . …… 6分
. …… 6分
(Ⅱ)由题设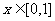 时,恒有
时,恒有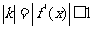 ,
,
即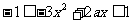 在
在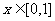 上恒成立.
……8分
上恒成立.
……8分
当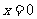 时,
时,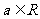 ;
;
当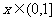 时,由
时,由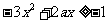 恒成立,即
恒成立,即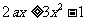 ,
,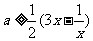 ,所以
,所以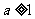 (函数
(函数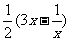 在
在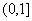 上为增函数). …… 10分
上为增函数). …… 10分
另一方面,由 恒成立,
恒成立,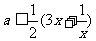 ,
,
所以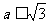 (当且仅当
(当且仅当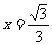 时,取最值).
时,取最值).
综上所述: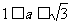 .
……12分
.
……12分
20. (本小题满分12分)(理科) (理科)有两辆汽车由南向北驶入四叉路口,各车向左转,向右转或向前行驶的概率相等,且各车的驾驶员相互不认识.
(I)规定:“第一辆车向左转,第二辆车向右转”这一基本事件用“(左,右)”表示。又“(直,左)”表示的是基本事件:“第一辆车向前直行,第二车向左转”.请参照上面规定列出两辆汽车过路口的所有基本事件;
(II)求至少有一辆汽车向左转的概率;
(III) 设有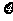 辆汽车向左转,求
辆汽车向左转,求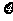 的分布列和数学期望.
的分布列和数学期望.
答案: (I) (左,左);(左,直);(左,右);
(直,右);(直,左);(直,直);
(右,右);(右,直);(右,左)
基本事件共有9种. ……4分
(II)至少有一辆汽车向左转的事件数有5种,
所求概率P= 5/9. ……8分
(III)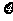 的分布列为
的分布列为
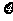 |
0 |
1 |
2 |
|
P |
4/9 |
4/9 |
1/9 |
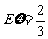 .
……12分
.
……12分
(文科)2009年6月1日起颁布实施的《食品安全法》取消了食品免检,某品牌10箱食品在出厂前进行质量检测,已知其中有2箱是次品.
(I)任意取出2箱进行检测,求其中至少有一箱是次品的概率;
(II)为了保证使2箱次品全部被检测出的概率不低于0.6,最少应抽取几箱产品做检测?
答案:(I)取出2箱进行检测,全是正品的概率为 ,至少有一箱是次品的概率为
,至少有一箱是次品的概率为
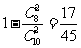 .
…………4分
.
…………4分
(II)设至少应抽取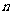 箱产品做检验,则
箱产品做检验,则
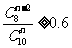 …………8分
…………8分
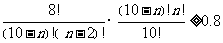 ,
,
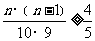 ,
,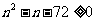 ,
, 或
或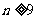 .…………12分
.…………12分
因此,最少应抽取9箱产品做检测才能保证使2箱次品全部被检测出的概率不低于0.8. …………12分
19. (本小题满分12分)(理科)已知数列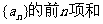
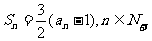
(Ⅰ)求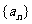 的通项公式;
的通项公式;
(Ⅱ)设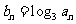 ,求数列
,求数列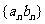 的前
的前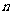 项和.
项和.
答案:(Ⅰ)因为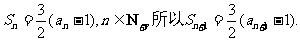
两式相减,得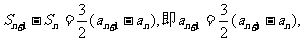
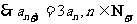 ………………3分
………………3分
又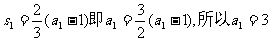
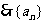 是首项为3,公比为3的等比数列。
是首项为3,公比为3的等比数列。
从而 ………………6分
………………6分
(Ⅱ)由(Ⅰ)知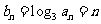 ,设数列
,设数列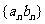 的前
的前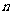 项和为
项和为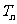 ,
,
则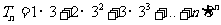 ,
,
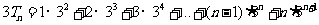 ,
,
两式相减得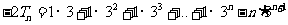 ………………10分
………………10分
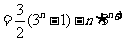 ,
,
所以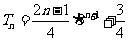 .
………………12分
.
………………12分
(文科)已知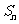 是数列
是数列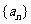 的前
的前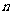 项和,
项和,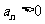 ,
,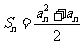 ,
,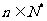 ,
,
(Ⅰ)求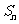

(Ⅱ)若数列 满足
满足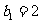 ,
,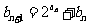 ,求
,求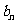

答案:(Ⅰ)当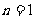 时,
时,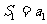
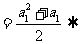
 .由
.由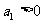 ,得
,得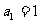
当 时,
时, 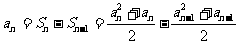 … …3分
… …3分
整理得
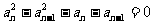 ,
, 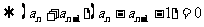
由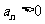 ,只有
,只有 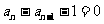 ,即
,即 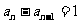
所以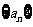 是
是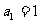 ,公差为
,公差为 的等差数列,
的等差数列, 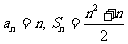 ……6分
……6分
(Ⅱ) 由(Ⅰ)得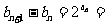
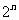
所以
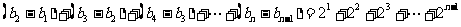
…… 9分
即 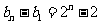 ,
,
又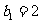 ,所以
,所以 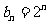 ……12分
……12分
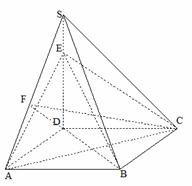
18. (本小题满分12分)(理科) 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,
(本小题满分12分)(理科) 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,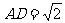 ,E是SD上的点.
,E是SD上的点.
(Ⅰ)求证:AC⊥BE;
(Ⅱ)求二面角C-AS-D的余弦值.
答案: (理科)法一:(Ⅰ)连结BD.因为底面ABCD是正方形,所以AC⊥BD.
 因为SD⊥平面ABCD,AC
因为SD⊥平面ABCD,AC 平面ABCD,
平面ABCD,
所以AC⊥SD.………………………2分
又因为SD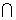 BD=D,
BD=D,
所以AC⊥平面BDS.………………4分
因为BE 平面BDS,
平面BDS,
所以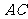 ⊥
⊥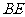 .……………………6分
.……………………6分
(Ⅱ)因为SD⊥平面ABCD,所以SD⊥CD.
因为底面ABCD是正方形,所以AD⊥CD.
又因为SD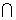 AD=D,所以CD⊥平面SAD,
AD=D,所以CD⊥平面SAD,
所以CD⊥AS.………………………8分
过点D在平面SAD内作DF⊥AS于F,连结CF.
由于,DF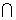 CD=D,所以AS⊥平面DCF。所以AS⊥CF.
CD=D,所以AS⊥平面DCF。所以AS⊥CF.
故∠CFD是二面角C-AS-D的平面角.………………………………………10分
在Rt△ADS中, ,
,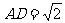 ,可求得
,可求得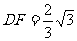 .
.
在Rt△CFD中,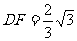 ,
,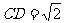 ,可求得
,可求得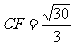 .
.
所以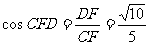 .即二面角C-AS-D的余弦值为
.即二面角C-AS-D的余弦值为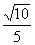 .………………12分
.………………12分
法二:(Ⅰ)如图以D为原点建立空间直角坐标系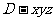 .则D(0,0,0),A(
.则D(0,0,0),A( ,0,0),B(
,0,0),B( ,
, ,0),C(0,
,0),C(0, ,0),E(0,0,
,0),E(0,0, ),S(0,0,2),
),S(0,0,2),
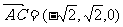 ,
,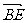 =
=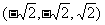 .…………………3分
.…………………3分
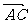 ·
·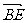 =2-2+0=0,所以
=2-2+0=0,所以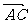 ⊥
⊥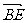 .即AC⊥BE.…………………………………6分
.即AC⊥BE.…………………………………6分
(Ⅱ)由(Ⅰ)得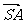 =(
=( ,0,-2),
,0,-2),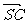 =(0,
=(0, ,-2).
,-2).
设平面ACS的法向量为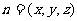 ,
,
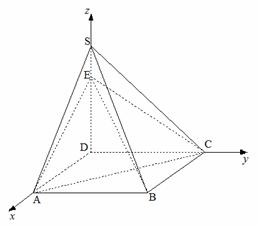 则由n⊥
则由n⊥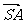 ,n⊥
,n⊥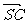 得
得
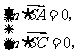
即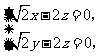
取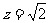 ,得
,得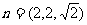 .…………………………………………………9分
.…………………………………………………9分
易知平面ASD的一个法向量为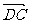 =(0,
=(0, ,0).
,0).
设二面角C-AS-D的平面角为θ.则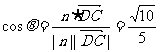 .
.
即二面角C-AS-D的余弦值为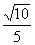 .…………………………………………12分
.…………………………………………12分
 (文科)在直三棱柱
(文科)在直三棱柱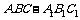 中,
中,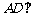 平面
平面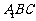 ,其垂足
,其垂足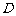 落在直线
落在直线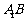 上.
上.
(Ⅰ)求证: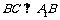 ;
;
(Ⅱ)若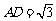 ,
,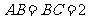 ,
,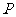 为
为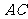 的中点,求三棱锥
的中点,求三棱锥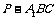 的体积.
的体积.
答案: (Ⅰ) 三棱柱
三棱柱 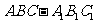 为直三棱柱,
为直三棱柱,
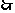
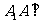 平面
平面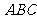 ,又
,又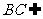 平面
平面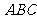 ,
,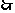
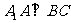 -----------------------------------2分
-----------------------------------2分

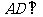 平面
平面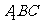 ,且
,且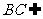 平面
平面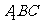 ,
,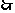
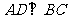 .
.
又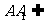 平面
平面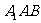 ,
,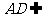 平面
平面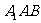 ,
,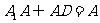 ,
,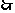
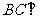 平面
平面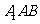 ,--------------5分
,--------------5分
又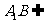 平面
平面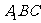 ,
,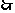
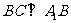 -----------------------------------6分
-----------------------------------6分
(Ⅱ)在直三棱柱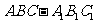 中,
中,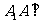
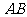 .
.
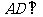 平面
平面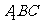 ,其垂足
,其垂足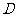 落在直线
落在直线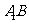 上,
上,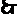
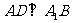 .
.
在 中,
中,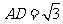 ,
,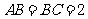 ,
,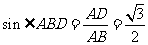 ,
,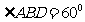 ,
,
在 中,
中, 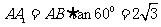 -----------------------------------8分
-----------------------------------8分
由(Ⅰ)知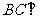 平面
平面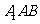 ,
,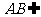 平面
平面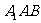 ,从而
,从而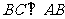 ,
,
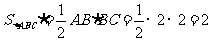 .
.

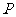 为
为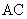 的中点,
的中点,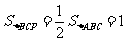 -----------------------10分
-----------------------10分
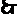
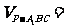
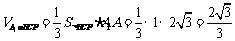 ---------------------12分
---------------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com