
21. (本小题满分12分)(理科) 已知椭圆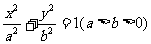 的左右焦点分别为
的左右焦点分别为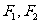 ,短轴两个端点为
,短轴两个端点为 ,且四边形
,且四边形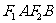 是边长为2的正方形.
是边长为2的正方形.
(I)求椭圆方程;
(II)若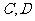 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点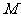 满足
满足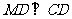 ,连接
,连接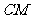 ,交椭圆于点
,交椭圆于点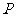 .求证:
.求证: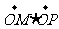 为定值.
为定值.
答案:(I)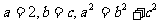 ,
, ,
,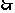 椭圆方程为
椭圆方程为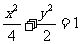 .
.
…………………………………………………………4分
(II)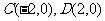 ,设
,设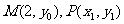 ,则
,则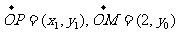 .
.
直线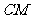 :
: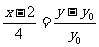 ,
,
即 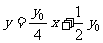 ,……………………………6分
,……………………………6分
代入椭圆 , 得
, 得
 。……………………………………………8分
。……………………………………………8分
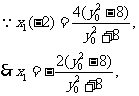
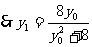 .
.
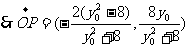 ,………………………………………………10分
,………………………………………………10分

 (定值).……………………12分
(定值).……………………12分
(文科)已知实数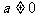 ,函数
,函数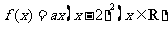 .
.
(Ⅰ)若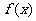 的图象在点
的图象在点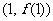 处的切线与直线
处的切线与直线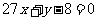 平行,求函数
平行,求函数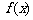 的极值;
的极值;
(Ⅱ)若对任意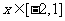 ,不等式
,不等式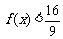 恒成立,求实数
恒成立,求实数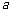 的取值范围.
的取值范围.
答案:(Ⅰ)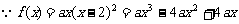 ,
,
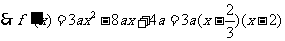 .
.
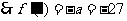 ,得
,得
 ------------2分
------------2分
令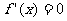 得
得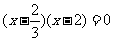 ,∴
,∴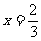 或
或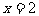 .
.
又函数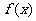 在
在 上为增函数,在
上为增函数,在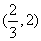 上为减函数,
上为减函数,
在 上为增函数------------4分
上为增函数------------4分
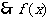 在
在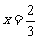 时取得极大值 ,
时取得极大值 ,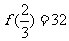 .
.
在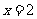 时取得极小值
时取得极小值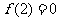 ------------6分
------------6分
(Ⅱ)由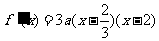 ,知
,知
当 时,函数
时,函数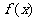 在
在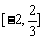 上是增函数,在
上是增函数,在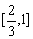 上是减函数.
上是减函数.
此时,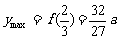 . 又对
. 又对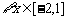 ,不等式
,不等式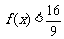 恒成立 .
恒成立 .
∴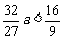 ,得
,得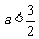 ,
,
∴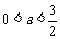 . ------------9分
. ------------9分
当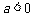 时,函数
时,函数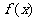 在
在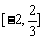 上是减函数,在
上是减函数,在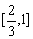 上是增函数.
上是增函数.
又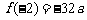 ,
,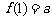 , 此时,
, 此时,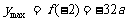 .
.
又对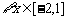 ,不等式
,不等式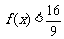 恒成立 .
恒成立 .
∴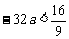 得
得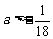 , ∴
, ∴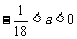 .
.
故所求实数的取值范围是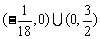 . ---------------12分
. ---------------12分
20. (本小题满分12分)(理科)已知数列{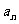 }满足
}满足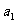 =2,
=2,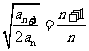 .
.
(I)求数列{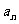 }的通项公式;
}的通项公式;
(II)设 ,试推断是否存在常数A,B,C,使对一切
,试推断是否存在常数A,B,C,使对一切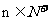 都有
都有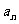 =
=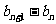 成立?若存在,求出A,B,C的值,若不存在,说明理由.
成立?若存在,求出A,B,C的值,若不存在,说明理由.
答案:(I) 由已知,得 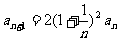 ,
,
即 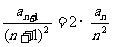 , ………………………3分
, ………………………3分
所以数列{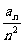 }是公比为2的等比数列,首项为
}是公比为2的等比数列,首项为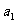 =2,
=2,
故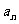 =
=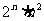 . ………………………6分
. ………………………6分
也可以用累积法
(II) 因为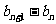 =
=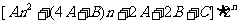 ,
,
若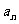 =
=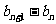 恒成立,则
恒成立,则 恒成立,所以
恒成立,所以
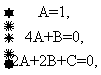 ………………………9分
………………………9分
解出 A=1,B=-4,C=6.
故存在常数A,B,C满足条件. ………………………12分
(文科)已知等差数列 和等比数列
和等比数列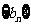 ,
,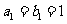 且
且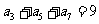 ,
,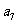 是
是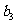 和
和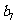 的等比中项.
的等比中项.
(Ⅰ)求数列 、
、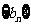 的通项公式;
的通项公式;
(Ⅱ)若 ,求数列
,求数列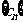 的前
的前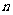 项和
项和 .
.
答案:(Ⅰ)设等差数列 的公差为
的公差为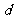 ,等比数列
,等比数列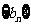 的公比为
的公比为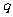 ,由题意知:
,由题意知:
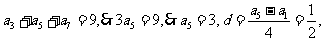
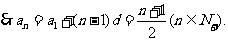 …………4分
…………4分
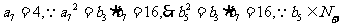 ,
,
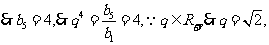
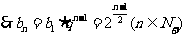 . …………6分
. …………6分
(II) 因为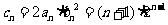 , …………8分
, …………8分
所以 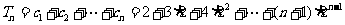 . (1)
. (1)
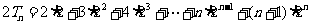 . (2) …………10分
. (2) …………10分
由(1)减(2), 得
 ,
,
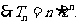 …………12分
…………12分
19. (本小题满分12分)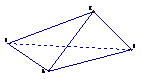
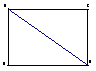 已知矩形ABCD中,
已知矩形ABCD中,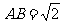 ,
,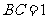 ,现沿对角线
,现沿对角线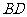 折成二面角
折成二面角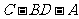 ,使
,使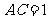 (如图).
(如图).
(I)求证: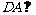 面
面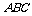 ;
;
(II)求二面角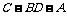 平面角的大小.
平面角的大小.
答案:(I)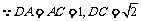 ,
,
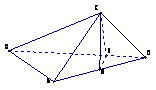
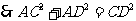 ,
,
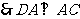 . …………3分
. …………3分
又 ,
,
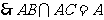
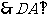 平面
平面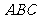 . …………6分
. …………6分
(II)方法一:取AB中点M,连CM,过M作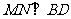 交BD于N,连CN.
交BD于N,连CN.

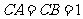 ,
,
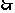
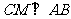 ,
,
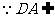 平面
平面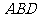 ,
,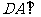 平面
平面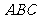 ,
,
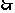 平面
平面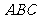
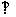 平面
平面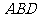 . …………8分
. …………8分
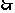
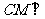 平面
平面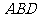 ,
,
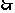
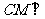
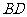 .
.
又
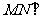
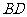 ,
,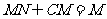
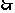
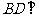 平面
平面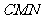 ,
,
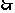

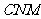 为二面角
为二面角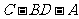 的平面角. …………10分
的平面角. …………10分
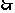
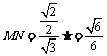 ,
,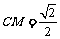 ,
,
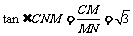 ,
,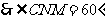 ,
,
故二面角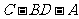 平面角的度数为
平面角的度数为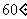 . …………12分
. …………12分
方法二:取AB中点M,连CM.
∵AC=AB=1, ∴CM⊥AB.
又∵平面ABC⊥平面ABD,∴CM⊥平面ABD.
取BD中点H,∴MH∥AD.
∵AD⊥AB, ∴MH⊥AB.
分别以AB,MH,MC为x,y,z轴建立空间直角坐标系. …………6分
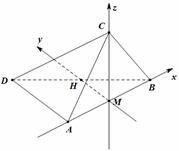 得
得 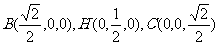 ,
,
∴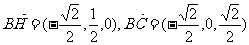 .
.
…………8分
设平面BCD的法向量为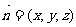 ,
,
∴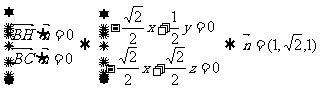 .
…………10分
.
…………10分
又∵平面ABD的法向量为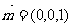 ,
,
∴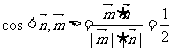
显然二面角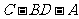 为锐角,所以它的大小为
为锐角,所以它的大小为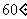 . …………12分
. …………12分
18. (本小题满分12分)为了让更多的人参与2010年在上海举办的“世博会”,上海某旅游公司面向国内外发行总量为2000万张的旅游优惠卡,其中向境外人士发行的是世博金卡(简称金卡),向境内人士发行的是世博银卡(简称银卡)。现有一个由36名游客组成的旅游团到上海参观旅游,其中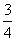 是境外游客,其余是境内游客。在境外游客中有
是境外游客,其余是境内游客。在境外游客中有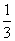 持金卡,在境内游客中有
持金卡,在境内游客中有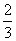 持银卡.
持银卡.
(I)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(II)在该团的境内游客中随机采访3名游客,设其中持银卡人数为随机变量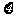 ,求
,求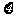 的分布列及数学期望
的分布列及数学期望 .
.
答案:(I)由题意得,境外游客有27人,其中9人持金卡;境内游客有9人,其中6人持银卡.设事件 为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
为“采访该团3人中,恰有1人持金卡且持银卡者少于2人”,
事件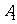 为“采访该团3人中,1人持金卡,0人持银卡”,
为“采访该团3人中,1人持金卡,0人持银卡”,
事件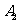 为“采访该团3人中,1人持金卡,1人持银卡”。
为“采访该团3人中,1人持金卡,1人持银卡”。 
 .
. 
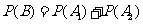
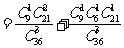 ………………………………………………………3分
………………………………………………………3分
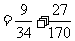
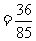
所以,在该团中随机采访3人,恰有1人持金卡且持银卡者少于2人的概率是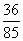 。
。
…………………………………………………………6分
(II)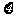 的可能取值为0,1,2,3
的可能取值为0,1,2,3
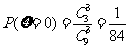 ,
,  .
. 

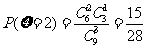 ,
,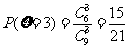 ,.
,. 

所以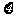 的分布列为
的分布列为
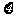 |
0 |
1 |
2 |
3 |
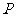 |
 |
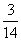 |
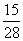 |
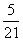 |
…………………………………………………………10分
所以 , ……………………12分
, ……………………12分
(文科)高考数学考试中共有12道选择题,每道选择题都有4个选项,其中有且仅有一个是正确的。评分标准规定:“在每小题给出的上个选项中,只有一项是符合题目要求的,答对得5分,不答或答错得0分”。某考生每道选择都选出一个答案,能确定其中有8道题的答案是正确的,而其余题中,有两道题都可判断出两个选项错误的,有一道题可能判断一个选项是错误的,还有一道题因不理解题意只能乱猜。试求出该考生的选择题:
(I)得60分的概率;
(II)得多少分的概率最大?
答案:(I)要得60分,必须12道选择题全答对. …………2分
依题意,易知在其余的四道题中,有两道题答对的概率各为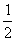 ,有一道题答对的概率为
,有一道题答对的概率为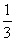 ,还有一道题答对的概率为
,还有一道题答对的概率为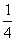 ,所以他做选择题得60分的概率为:
,所以他做选择题得60分的概率为:
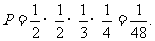 …………6分
…………6分
(II)依题意,该考生选择题得分的可能取值有:40,45,50,55,60共五种
得分为40,表示只做对有把握的那8道题,其余各题都做错,于是其概率为:
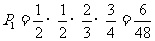 .
.
类似的,可知得分为45分的概率:
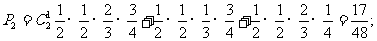
得分为50的概率: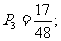
得分为55的概率: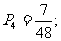
得分为60的概率: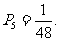
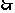 该生选择题得分为45分或50分的可能性最大. …………12分
该生选择题得分为45分或50分的可能性最大. …………12分
请把解答过程写在答题卡相应位置上.)
17. (本小题满分10分)已知a、b、c是△ABC三边长,关于x的方程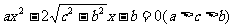 的两根之差的平方等于4,△ABC的面积
的两根之差的平方等于4,△ABC的面积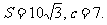
(I)求 C;
C;
(II)求a、b的值.
答案:(I)设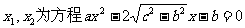 的两根.
的两根.
则 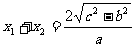 ,
, .
……………………………2分
.
……………………………2分
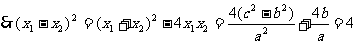 .
.
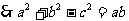 .
………………………………4分
.
………………………………4分
又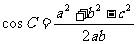 ,
,
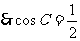 ,
,
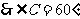 .
…………………………………………6分
.
…………………………………………6分
(II)由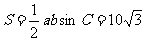 ,
,
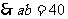 . ①
. ①
由余弦定理 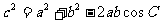 ,
,
即 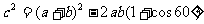 ,
,
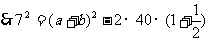 ,
,
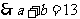 . ②
……………………………8分
. ②
……………………………8分
由①、②,得 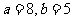 . …………………………………10分
. …………………………………10分
16. (理科)秋末冬初,流感盛行,特别是甲型H1N1流感传染性强.重庆市某医院近30天每天入院治疗甲流的人数依次构成数列{a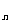 },已知a
},已知a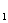 =1,a
=1,a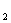 =2,且
=2,且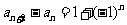 (n∈N
(n∈N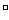 ),则该医院30天入院治疗甲流感的人数共有 .
),则该医院30天入院治疗甲流感的人数共有 .
答案:255. 由于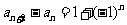 ,所以
,所以 ,
,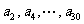 构成公差为2的等差数列,所以
构成公差为2的等差数列,所以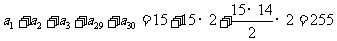 .
.
(文科)某企业三月中旬生产A、B、C三种产品共3000件,根据分层抽样的结果;企业统计员制作了如下的统计表格:
|
产品类别 |
A |
B |
C |
|
产品数量(件) |
|
1300 |
|
|
样本容量(件) |
|
130 |
|
由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是 件.
答案:800.
15. 已知球O是棱长为12的正四面体S-ABC的外接球,D,E,F分别是棱SA,SB,SC的中点,则平面DEF截球O所得截面的面积是_______.
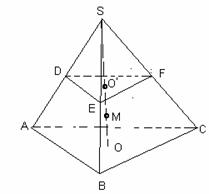 答案:48
答案:48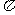 .作图如右,设M点球心,可为高SO的四等分点处,
.作图如右,设M点球心,可为高SO的四等分点处,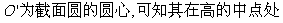 ,易求出
,易求出
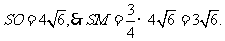
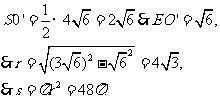
14. 设变量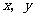 满足约束条件
满足约束条件 ,则目标函数
,则目标函数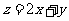 的最小值为______.
的最小值为______.
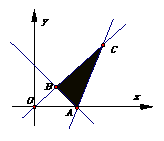 答案:3. 本题考查线性规划的有关知识,以及数形结合的数学思想方法.
答案:3. 本题考查线性规划的有关知识,以及数形结合的数学思想方法.
设变量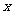 、
、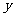 满足约束条件
满足约束条件 在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),则目标函数
在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),则目标函数
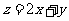 的最小值为3.
的最小值为3.
13. (理科)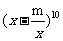 的展开式中,常数项为252,则
的展开式中,常数项为252,则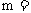 ______.
______.
答案: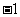 .注意到
.注意到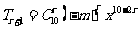 ,由
,由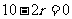 ,得
,得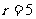 ,所以常数项是
,所以常数项是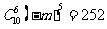 ,解得
,解得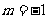 .
.
(文科)在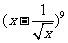 的展开式中,常数项是第___项.
的展开式中,常数项是第___项.
答案:7.
12. 两旅客坐火车外出旅游,希望座位连在一起,且有一个靠窗,已知火车上的座位的排法如右图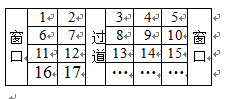 所示,则下列座位号码符合要求的应当是(
).
所示,则下列座位号码符合要求的应当是(
).
A. 48,49 B. 62,63
C. 75,76 D. 84,85
答案: D. 通过逻辑推理与分析,容易知道, 只有D符合条件.
第Ⅱ卷(非选择题,共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com