
3. 2009年,有3位科学家因构建了显示不同抗生素是如何抑制核糖体功能的三维模型而获得诺贝尔化学奖。下列有关说法错误的是( )
A.抑制细菌核糖体的功能,细菌就难以存活
B.三维模型可用于研发新抗生素和治疗疾病
C.三维模型的构建与蛋白质和RNA的空间结构相关
D.核糖体中的核酸是其自身蛋白质合成的直接模板
2.下图表示植物细胞的部分结构及其生理功能。下列有关叙述中,正确的是( )
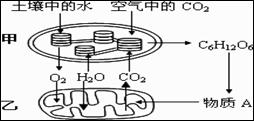 A.图示状态表示光合作用速率小于呼吸作 用速率
A.图示状态表示光合作用速率小于呼吸作 用速率
B.甲中不含有而乙中含有将ADP转变成ATP的酶
C.在甲中随水的分解产生[H],在乙中随 水的产生消耗[H]
D.C6H12O6可以在乙中直接彻底氧化分解
1.研究人员测得沼气池中两种代谢类型的细菌的数量变化如图。下列说法不正确的是( )
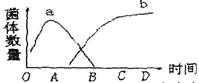 A.a代表好氧性细菌,b代表厌氧性细菌
A.a代表好氧性细菌,b代表厌氧性细菌
B.在OB时间段内,a类细菌的种内斗争逐渐增强
C.在沼气池这个生态系统中,两类细菌很可能都属于 分解者
D.细菌a的生命活动为细菌b的大量繁殖创造了条件
6、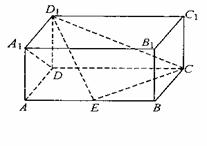 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D;
(2)当E为AB的中点时,求点A到面ECD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为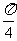 .
.
(1)证明:连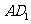 ,在长方体ABCD-A1B1C1D1中,
,在长方体ABCD-A1B1C1D1中,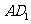 为
为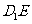 在平面
在平面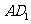 的射影,
的射影,
而AD=AA1=1,则四边形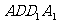 是正方形
是正方形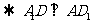 ,
,
由三垂线定理得D1E⊥A1D ……………3分
(2)点A到面ECD1的距离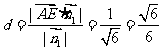 ……………7分
……………7分
(3)当AE=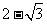 时,二面角D1-EC-D的大小为
时,二面角D1-EC-D的大小为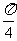 。……………12分
。……………12分
5、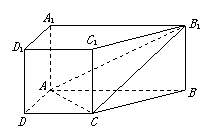 直棱柱
直棱柱 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形,
∠BAD=∠ADC=90°,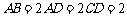 .
.
(Ⅰ)求证:AC⊥平面BB1C1C;
(Ⅱ)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
证明:(Ⅰ) 直棱柱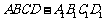 中,BB1⊥平面ABCD,
中,BB1⊥平面ABCD,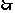 BB1⊥AC.
BB1⊥AC.
又 ∠BAD=∠ADC=90°,
∠BAD=∠ADC=90°,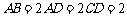 ,
,
∴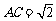 ,∠CAB=45°,∴
,∠CAB=45°,∴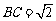 ,
,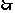 BC⊥AC分
BC⊥AC分
又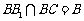 ,
,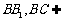 平面BB1C1C,
平面BB1C1C,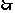 AC⊥平面BB1C1C.
AC⊥平面BB1C1C.
(Ⅱ)存在点P,P为A1B1的中点.
证明:由P为A1B1的中点,有PB1‖AB,且PB1= AB.
AB.
又∵DC‖AB,DC= AB,
AB,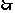 DC ∥PB1,且DC= PB1,
DC ∥PB1,且DC= PB1,
∴DC PB1为平行四边形,从而CB1∥DP.
又CB1 面ACB1,DP
面ACB1,DP  面ACB1,
面ACB1,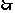 DP‖面ACB1.
DP‖面ACB1.
同理,DP‖面BCB1.
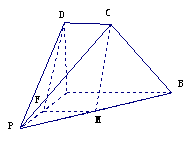
4、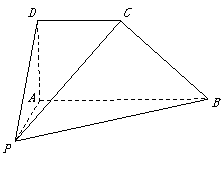 如图,在四棱锥P-ABCD中,CD//AB
, AD⊥AB ,
如图,在四棱锥P-ABCD中,CD//AB
, AD⊥AB ,
AD = DC = AB , BC⊥PC.
(1)求证:PA⊥BC ;
(2)试在线段PB上找一点M,使CM // 平面PAD, 并说明理由.
解:(1)连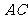 ,在四边形ABCD中,
,在四边形ABCD中,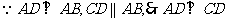 .
.
设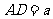 ,
,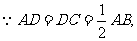
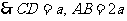 .
.
 在
在 中,
中, ,
,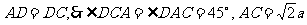
在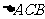 中,
中,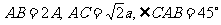
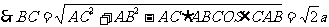 .
.
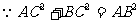 ,
,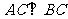
又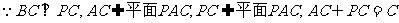 ,
,
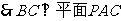

(2)当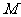 为
为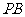 的中点时,
的中点时,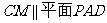
取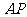 的中点
的中点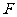 ,连结
,连结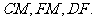 则
则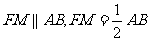 .
.
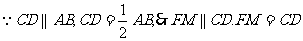
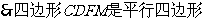 ,
,
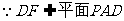 ,
,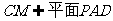 ,
,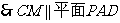 .
.
3、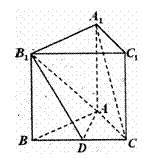 如图,正三棱柱
如图,正三棱柱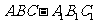 中,
中,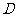 是
是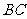 的中点,
的中点,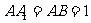
(Ⅰ)求证: ∥平面
∥平面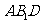 ;
;
(Ⅱ)求二面角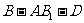 的大小。
的大小。
(Ⅰ)证明:连接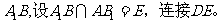
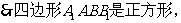
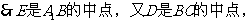
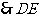 ∥
∥ 。 ……………………3分
。 ……………………3分
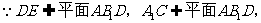
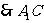 ∥平面
∥平面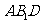 …………………………5分
…………………………5分
(Ⅱ)解:在平面
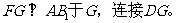
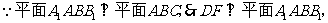
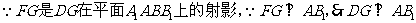
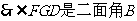 -
-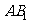 -
-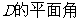 ……………………8分
……………………8分
设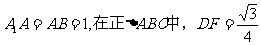 。
。
在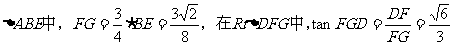
所以,二面角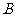 -
-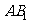 -
-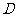 的大小为
的大小为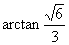 。 ………………12分
。 ………………12分
是否存在问题
2、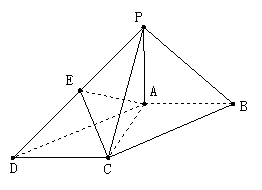 如图,在底面为平行四边形的四棱锥
如图,在底面为平行四边形的四棱锥 中,
中,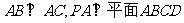 ,且
,且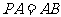 ,点
,点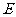 是
是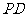 的中点。
的中点。
⑴求证: ;
;
⑵求证: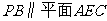 ;
;
⑶求二面角 的大小。
的大小。

1、 (高考模拟)在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足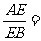
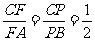 (如图1).将△AEF沿EF折起到
(如图1).将△AEF沿EF折起到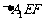 的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
的位置,使二面角A1-EF-B成直二面角,连结A1B、A1P(如图2)
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示).

解:不妨设正三角形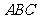 的边长为3,则
的边长为3,则
(1)在图1中,取 中点
中点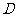 ,连结
,连结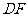 ,
,
则∵ 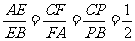 ,
,
∴ 而
而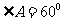 ,即△
,即△
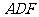 是正三角形
是正三角形
又∵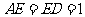 , ∴
, ∴
∴在图2中有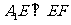 ,
,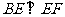 ,
,
∴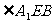 为二面角
为二面角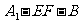 的平面角
的平面角
∵二面角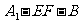 为直二面角, ∴
为直二面角, ∴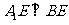
又∵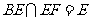 , ∴
, ∴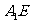 ⊥平面
⊥平面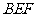 ,即
,即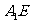 ⊥平面
⊥平面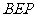 .
.
(2)直线A1E与平面A1BP所成角的大小为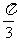 .
.
(3)二面角B-A1P-F为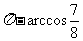 .
.
[方法探究]本题属于翻折问题,在翻折前的图1中易证EF⊥AB,而翻折后保持这一垂直关系,并且易证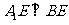 .
.
[技巧点拨]本题属于翻折问题,这是高考的热点题型. 求解翻折问题的策略是对比翻折前后,分析变与不变,一般地有:(1)分析翻折前后点的变化,注意点与点的重合问题以及点的位置的改变;(2)分析翻折前后长度与角度的变化,注意利用平面图形解决空间的线段长度以及空间角的大小;(3)若翻折后,线与线仍同在一个平面内,则它们的位置关系不发生任何变化;若翻折后,线与线由同一平面转为不同平面,则应特别注意点的位置变化.
关系求证和解二面角
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com