
7.近代史上,顽固派“其貌则孔也,其心则夷也”的指责主要针对下列哪位人物的思想主张?
A.魏源 B.李鸿章 C.康有为 D.孙中山
解析:“其貌则孔也,其心则夷也”说明此人表面推崇孔子,实质宣扬西方资产阶级民主思想。康有为打着孔子的旗号宣传维新变法的思想。故正确答案为C。
6.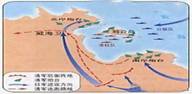 右图展示了近代某一次重要战役,对此叙述正确的是
右图展示了近代某一次重要战役,对此叙述正确的是
A.战役结束后清舰队全军覆没
B.清朝军民反割台斗争的关键战役
C.清军将领邓世昌于此役壮烈殉国
D.战役发生于清军运兵朝鲜途中
解析:图片展示的是威海卫战役。威海卫战役中,北洋舰队全军覆没。故正确答案为A。
5.“圣人不责人之必能,是以人人皆可以为圣。”这句话最符合下列哪位思想家的主张?
A.朱熹 B.李贽 C.陆九渊 D.黄宗羲
解析:“人人皆可以为圣”对孔子及儒家思想的正统地位提出了挑战。故正确答案为B。
4.东汉南阳太守杜诗“造作水排,铸为农器,用力少,见功多,百姓便之”,“水排”主要应用于
A.灌溉 B.制瓷 C.耕种 D.冶铁
解析:东汉南阳太守杜诗发明水力鼓风冶铁工具--水排。故正确答案为D。
3.“元起朔方,固已崇尚释教(佛教),及得西域,世祖以地广而险远,……思有以因其俗而柔其人,乃郡县土番之地,设官分职,而领之于帝师。”这里的“官”隶属于
A.宣政院 B.中书省 C.理藩院 D.行中书省
解析: “土番”即吐蕃,也就是西藏地区。元朝在中央设立宣政院,统领宗教事务和管理西藏地区。故正确答案为A。
2.诗人左思在其《咏史》中浓郁悲歌:“世胄蹑高位,英俊沉下僚。地势使之然,由来非一朝。”造成这一社会状况的制度原因是
A.征辟制 B.察举制 C.九品中正制 D.科举制
解析:“世胄蹑高位,英俊沉下僚。”指的是世家大族子弟依靠门第即可出任高官,而真正有才学,但出身低微的人,只能做地位卑下的小官。很显然造成这一状况的制度原因是九品中正制。故正确答案为C。
1.柳宗元《封建论》载:“时有叛国而无叛郡,秦制之得,亦以明矣。”符合这一论断的历史时期是
A.秦朝 B.西汉 C.南北朝 D.唐朝
解析:汉初在地方实行郡国并行制。故正确答案为B。
23、(本小题满分10分)
已知△ABC的三边长都是有理数。
(1)求证cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数。
[解析] 本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。
(方法一)(1)证明:设三边长分别为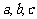 ,
, ,∵
,∵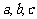 是有理数,
是有理数,
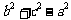 是有理数,分母
是有理数,分母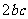 为正有理数,又有理数集对于除法的具有封闭性,
为正有理数,又有理数集对于除法的具有封闭性,
∴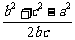 必为有理数,∴cosA是有理数。
必为有理数,∴cosA是有理数。
(2)①当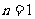 时,显然cosA是有理数;
时,显然cosA是有理数;
当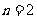 时,∵
时,∵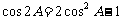 ,因为cosA是有理数, ∴
,因为cosA是有理数, ∴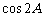 也是有理数;
也是有理数;
②假设当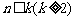 时,结论成立,即coskA、
时,结论成立,即coskA、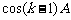 均是有理数。
均是有理数。
当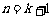 时,
时,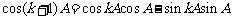 ,
,
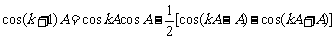 ,
,
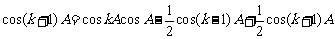 ,
,
解得: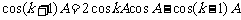
∵cosA,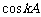 ,
,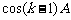 均是有理数,∴
均是有理数,∴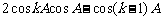 是有理数,
是有理数,
∴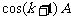 是有理数。
是有理数。
即当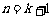 时,结论成立。
时,结论成立。
综上所述,对于任意正整数n,cosnA是有理数。
(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知
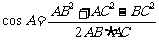 是有理数。
是有理数。
(2)用数学归纳法证明cosnA和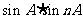 都是有理数。
都是有理数。
①当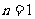 时,由(1)知
时,由(1)知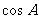 是有理数,从而有
是有理数,从而有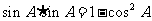 也是有理数。
也是有理数。
②假设当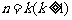 时,
时,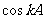 和
和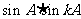 都是有理数。
都是有理数。
当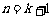 时,由
时,由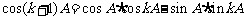 ,
,
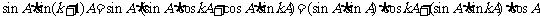 ,
,
及①和归纳假设,知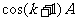 和
和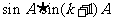 都是有理数。
都是有理数。
即当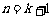 时,结论成立。
时,结论成立。
综合①、②可知,对任意正整数n,cosnA是有理数。
22、(本小题满分10分)
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
[解析] 本题主要考查概率的有关知识,考查运算求解能力。满分10分。
解:(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
|
X |
10 |
5 |
2 |
-3 |
|
P |
0.72 |
0.18 |
0.08 |
0.02 |
(2)设生产的4件甲产品中一等品有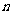 件,则二等品有
件,则二等品有 件。
件。
由题设知 ,解得
,解得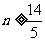 ,
,
又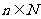 ,得
,得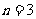 ,或
,或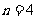 。
。
所求概率为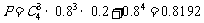
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
21. [选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A. 选修4-1:几何证明选讲
(本小题满分10分)
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
[解析] 本题主要考查三角形、圆的有关知识,考查推理论证能力。
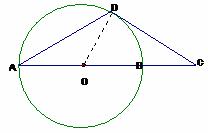 (方法一)证明:连结OD,则:OD⊥DC,
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
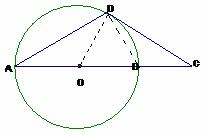 因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故AB=2BC。
B. 选修4-2:矩阵与变换
(本小题满分10分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
解:由题设得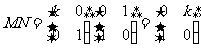
由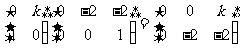 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1(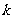 ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是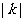 ,则由题设知:
,则由题设知: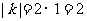 。
。
所以k的值为2或-2。
C. 选修4-4:坐标系与参数方程
(本小题满分10分)
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
[解析] 本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力。满分10分。
解: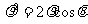 ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: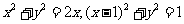 ,
,
直线3ρcosθ+4ρsinθ+a=0的普通方程为: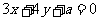 ,
,
又圆与直线相切,所以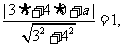 解得:
解得: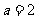 ,或
,或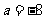 。
。
D. 选修4-5:不等式选讲
(本小题满分10分)
设a、b是非负实数,求证: 。
。
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明: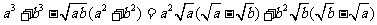
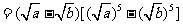
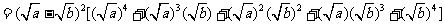
因为实数a、b≥0,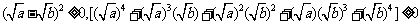
所以上式≥0。即有 。
。
(方法二)证明:由a、b是非负实数,作差得
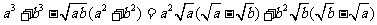
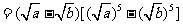
当 时,
时,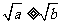 ,从而
,从而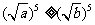 ,得
,得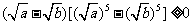 ;
;
当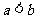 时,
时, ,从而
,从而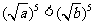 ,得
,得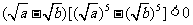 ;
;
所以 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com