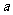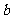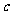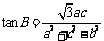6．在△ABC中，角A、B、C的对边分别为、、，且，则角B的大小是　 ★　 .

5．若不等式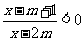成立的一个充分非必要条件是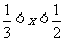，则实数的取值范围是　 ★　 .

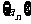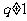4．各项都是正数的等比数列的公比，且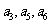成等差数列，则= 　★____.

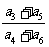3．某校高一、高二、高三共有3600名学生，其中高一学生1400名，高二学生1200名，高三学生1000名，现用分层抽样的方法抽取样本，已知抽取高一学生数为21，则每个学生被抽到的概率为 ★ .

2．已知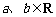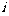，是虚数单位，若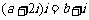，则a+b的值是 　★　 .

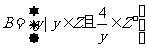1．若集合，，则集合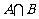的元素个数为　 ★　 .

22.在平面直角坐标系中，O为坐标原点，已知两点M(1，-3)、N(5，1)，若点C满足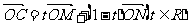，点C的轨迹与抛物线：y²=2px(p>0)交于D、E两点。

　 (1)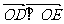，求抛物线的方程；

　 (2)过动点(a,0)且斜率为1的直线l与该抛物线交于不同的两点A、B，且|AB|2p。

　 (i)求a的取值范围；

　 (ii)若线段AB的垂直平分线交x轴于点Q，求QAB面积的最大值。

理科数学试题(二)第4页(共4页)

21.已知函数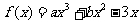在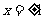处取得极值。

　 (1)求函数f(x)的解析式；

　 (2)求证；对于区间[-1，1]上任意两个自变量的值x₁，x₂，都有|f(x₁)-f(x₂)|4；

　 (3)若过点A(1,m)(m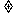-2)可作曲线y=f(x)的三条切线，求实数m的取值范围。

20.请看右边的程序框图：

　 若依次输入m=0,1,2,3,4,……，(m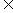N)，则由右边程序框图输出的数值A组成一个数列{a_n}。

　 (1)求a₁,a₂,a₃,a₄和数列{a_n}的通项公式；

　 (2)若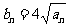，求数列{b_n}的前n项和S_n。

　 (1)求随机变量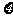的分布列及数学期望；

　 (2)设“函数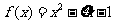在区间(2，3)上有且只有一个零点”为事件A，求事件A发生的概率。

　　　　　　　　　　　　 理科数学试题(二)第3页(共4页)

19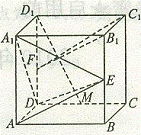．在正方体ABCD-A₁B₁C₁D₁中，E、F分别为棱BB₁和DD₁中点。

　 (1)求证：平面B₁FC₁//平面ADE；

　 (2)试在棱DC上求一点M，使D₁M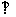平面ADE

　 (3)求二面角A₁-DE-A的余弦值。