
2.可根据内容要点适当发挥,但不要逐条翻译;
(17)(本小题满分10分)
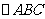 中,
中,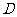 为边
为边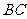 上的一点,
上的一点,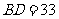 ,
,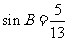 ,
,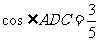 ,求
,求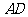 。
。
(18)(本小题满分12分)
已知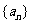 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
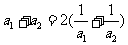 ,
,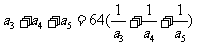
(Ⅰ)求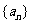 的通项公式;
的通项公式;
(Ⅱ)设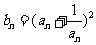 ,求数列
,求数列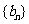 的前
的前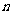 项和
项和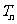 。
。
(19)(本小题满分12分)
如图,直三棱柱ABC-A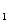 B
B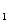 C
C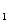 中,AC=BC, AA
中,AC=BC, AA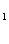 =AB,D为BB
=AB,D为BB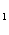 的中点,E为AB
的中点,E为AB 上的一点,AE=3 EB
上的一点,AE=3 EB
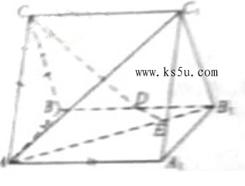 (Ⅰ)证明:DE为异面直线AB
(Ⅰ)证明:DE为异面直线AB 与CD的公垂线;
与CD的公垂线;
(Ⅱ)设异面直线AB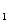 与CD的夹角为45°,求二面角A
与CD的夹角为45°,求二面角A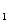 -AC
-AC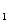 -B
-B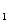 的大小
的大小
(20)(本小题满分12分)
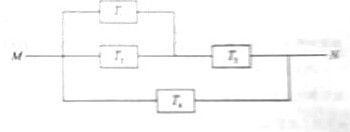
如图,由M到N的电路中有4个元件,分别标为T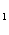 ,T
,T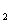 ,T
,T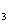 ,T
,T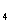 ,电源能通过T
,电源能通过T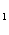 ,T
,T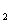 ,T
,T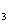 的概率都是P,电源能通过T
的概率都是P,电源能通过T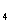 的概率是0.9,电源能否通过各元件相互独立。已知T
的概率是0.9,电源能否通过各元件相互独立。已知T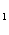 ,T
,T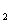 ,T
,T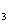 中至少有一个能通过电流的概率为0.999。
中至少有一个能通过电流的概率为0.999。
(Ⅰ)求P;
(Ⅱ)求电流能在M与N之间通过的概率。
(21)(本小题满分12分)
已知函数f(x)=x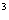 -3ax
-3ax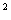 +3x+1。
+3x+1。
(Ⅰ)设a=2,求f(x)的单调期间;
(Ⅱ)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围。
(22)(本小题满分12分)
已知斜率为1的直线1与双曲线C: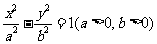 相交于B、D两点,且BD的中点为M(1.3)
相交于B、D两点,且BD的中点为M(1.3)
(Ⅰ)(Ⅰ)求C的离心率;
(Ⅱ)(Ⅱ)设C的右顶点为A,右焦点为F,|DF|·|BF|=17证明:过A、B、D三点的圆与x轴相切。
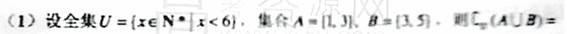
(A)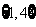 (B)
(B)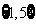 (C)
(C)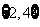 (D)
(D)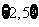
(2)不等式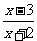 <0的解集为
<0的解集为
(A) (B)
(B)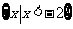 (C)
(C)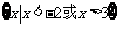 (D)
(D)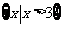
(3)已知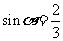 ,则
,则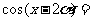
(A)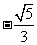 (B)
(B) (C)
(C)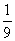 (D)
(D)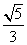
(4)函数y=1+(x-1)(x>1)的反函数是
(A)y=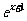 -1(x>0) (B) )y=
-1(x>0) (B) )y=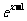 +1(x>0)
+1(x>0)
(C) y=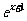 -1(x
-1(x 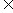 R) (D)y=
R) (D)y=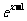 +1 (x
+1 (x
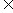 R)
R)
(5)若变量x,y满足约束条件 则z=2x+y的最大值为
则z=2x+y的最大值为
(A)1 (B)2 (C)3 (D)4
(6)如果等差数列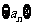 中,
中,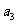 +
+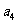 +
+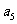 =12,那么
=12,那么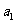 +
+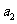 +•••…+
+•••…+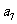 =
=
(A)14 (B) 21 (C) 28 (D) 35
(7)若曲线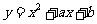 在点
在点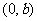 处的切线方程是
处的切线方程是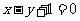 ,则
,则
(A)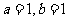 (B)
(B) 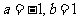
(C) 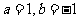 (D)
(D)
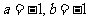
(8)已知三棱锥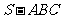 中,底面
中,底面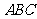 为边长等于2的等边三角形,
为边长等于2的等边三角形,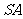 垂直于底面
垂直于底面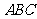 ,
,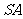 =3,那么直线
=3,那么直线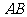 与平面
与平面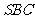 所成角的正弦值为
所成角的正弦值为
(A) 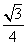 (B)
(B)
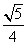
(C) 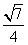 (D)
(D)
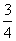
(9)将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有
(A) 12种 (B) 18种 (C) 36种 (D) 54种
(10)△ABC中,点D在边AB上,CD平分∠ACB,若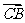 = a ,
= a , 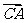 = b ,
= b , 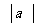 = 1 ,
= 1 ,
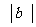 = 2, 则
= 2, 则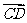 =
=
(A)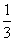 a +
a + 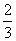 b (B)
b (B)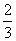 a +
a +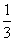 b (C)
b (C)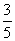 a +
a +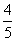 b
(D)
b
(D)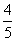 a +
a +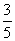 b
b
(11)与正方体ABCD-A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个
(12)已知椭圆C: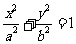 (a>b>0)的离心率为
(a>b>0)的离心率为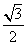 ,过右焦点F且斜率为k(k>0)的直线于C相交于A、B两点,若
,过右焦点F且斜率为k(k>0)的直线于C相交于A、B两点,若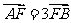 。则k =
。则k =
(A)1 (B) (C)
(C)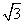 (D)2
(D)2
(13)已知α是第二象限的角,tanα=1/2,则cosα=__________
(14)(x+1/x)9的展开式中,x3的系数是_________
(15)已知抛物线C:y2=2px(p>0)的准线l,过M(1,0)且斜率为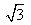 的直线与l相交于A,与C的一个交点为B,若
的直线与l相交于A,与C的一个交点为B,若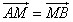 ,则p=_________
,则p=_________
(16)已知球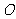 的半径为4,圆
的半径为4,圆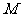 与圆
与圆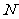 为该球的两个小圆,
为该球的两个小圆,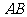 为圆
为圆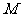 与圆
与圆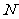 的公共弦,
的公共弦,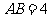 ,若
,若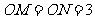 ,则两圆圆心的距离
,则两圆圆心的距离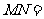 。
。
21、(本小题满分13分)
品酒师需定期接受酒味鉴别功能测试,一种通常采用的测试方法如下:拿出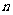 瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这
瓶外观相同但品质不同的酒让其品尝,要求其按品质优劣为它们排序;经过一段时间,等其记忆淡忘之后,再让其品尝这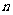 瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
瓶酒,并重新按品质优劣为它们排序,这称为一轮测试。根据一轮测试中的两次排序的偏离程度的高低为其评为。
现设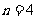 ,分别以
,分别以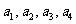 表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
表示第一次排序时被排为1,2,3,4的四种酒在第二次排序时的序号,并令
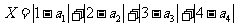 ,
,
则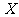 是对两次排序的偏离程度的一种描述。
是对两次排序的偏离程度的一种描述。
(Ⅰ)写出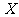 的可能值集合;
的可能值集合;
(Ⅱ)假设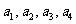 等可能地为1,2,3,4的各种排列,求
等可能地为1,2,3,4的各种排列,求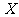 的分布列;
的分布列;
(Ⅲ)某品酒师在相继进行的三轮测试中,都有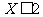 ,
,
(i)试按(Ⅱ)中的结果,计算出现这种现象的概率(假定各轮测试相互独立);
(ii)你认为该品酒师的酒味鉴别功能如何?说明理由。


全 品中考网
20、(本小题满分12分)
设数列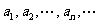 中的每一项都不为0。
中的每一项都不为0。
证明: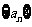 为等差数列的充分必要条件是:对任何
为等差数列的充分必要条件是:对任何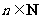 ,都有
,都有
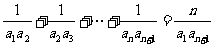 。
。
19、(本小题满分13分)
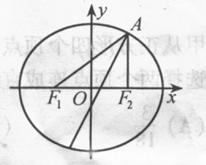 已知椭圆
已知椭圆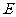 经过点
经过点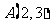 ,对称轴为坐标轴,焦点
,对称轴为坐标轴,焦点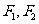 在
在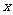 轴上,离心率
轴上,离心率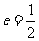 。
。
(Ⅰ)求椭圆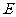 的方程;
的方程;
(Ⅱ)求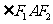 的角平分线所在直线
的角平分线所在直线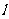 的方程;
的方程;
(Ⅲ)在椭圆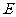 上是否存在关于直线
上是否存在关于直线 对称的相异两点?若存在,请找出;若不存在,说明理由。
对称的相异两点?若存在,请找出;若不存在,说明理由。
18、(本小题满分12分)
如图,在多面体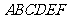 中,四边形
中,四边形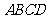 是正方形,
是正方形,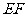 ∥
∥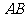 ,
,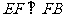 ,
,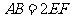 ,
,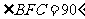 ,
,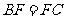 ,
, 为
为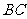 的中点。
的中点。
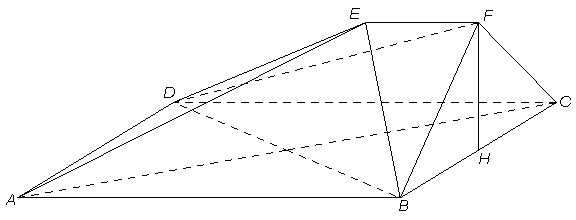
(Ⅰ)求证: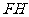 ∥平面
∥平面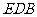 ;
;
(Ⅱ)求证: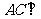 平面
平面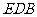 ;
;
(Ⅲ)求二面角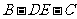 的大小。
的大小。
17、(本小题满分12分)
设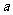 为实数,函数
为实数,函数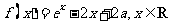 。
。
(Ⅰ)求 的单调区间与极值;
的单调区间与极值;
(Ⅱ)求证:当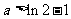 且
且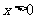 时,
时,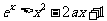 。
。
16、(本小题满分12分)
设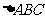 是锐角三角形,
是锐角三角形,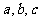 分别是内角
分别是内角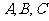 所对边长,并且
所对边长,并且
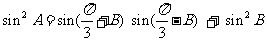 。
。
(Ⅰ)求角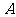 的值;
的值;
(Ⅱ)若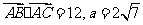 ,求
,求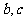 (其中
(其中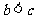 )。
)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com