
23、(本小题满分10分)
已知△ABC的三边长都是有理数。
(1)求证cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数。
[解析] 本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。
(方法一)(1)证明:设三边长分别为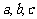 ,
,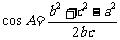 ,∵
,∵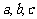 是有理数,
是有理数,
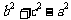 是有理数,分母
是有理数,分母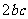 为正有理数,又有理数集对于除法的具有封闭性,
为正有理数,又有理数集对于除法的具有封闭性,
∴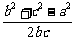 必为有理数,∴cosA是有理数。
必为有理数,∴cosA是有理数。
(2)①当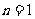 时,显然cosA是有理数;
时,显然cosA是有理数;
当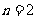 时,∵
时,∵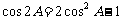 ,因为cosA是有理数, ∴
,因为cosA是有理数, ∴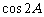 也是有理数;
也是有理数;
②假设当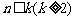 时,结论成立,即coskA、
时,结论成立,即coskA、 均是有理数。
均是有理数。
当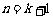 时,
时,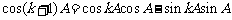 ,
,
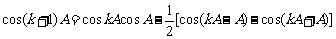 ,
,
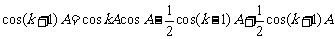 ,
,
解得: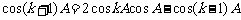
∵cosA,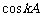 ,
, 均是有理数,∴
均是有理数,∴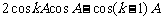 是有理数,
是有理数,
∴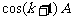 是有理数。
是有理数。
即当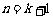 时,结论成立。
时,结论成立。
综上所述,对于任意正整数n,cosnA是有理数。
(方法二)证明:(1)由AB、BC、AC为有理数及余弦定理知
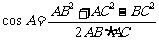 是有理数。
是有理数。
(2)用数学归纳法证明cosnA和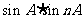 都是有理数。
都是有理数。
①当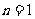 时,由(1)知
时,由(1)知 是有理数,从而有
是有理数,从而有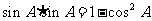 也是有理数。
也是有理数。
②假设当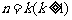 时,
时,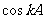 和
和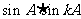 都是有理数。
都是有理数。
当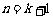 时,由
时,由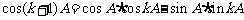 ,
,
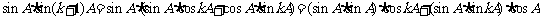 ,
,
及①和归纳假设,知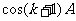 和
和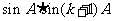 都是有理数。
都是有理数。
即当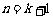 时,结论成立。
时,结论成立。
综合①、②可知,对任意正整数n,cosnA是有理数。
22、(本小题满分10分)
某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%。生产1件甲产品,若是一等品则获得利润4万元,若是二等品则亏损1万元;生产1件乙产品,若是一等品则获得利润6万元,若是二等品则亏损2万元。设生产各种产品相互独立。
(1)记X(单位:万元)为生产1件甲产品和1件乙产品可获得的总利润,求X的分布列;
(2)求生产4件甲产品所获得的利润不少于10万元的概率。
[解析] 本题主要考查概率的有关知识,考查运算求解能力。满分10分。
解:(1)由题设知,X的可能取值为10,5,2,-3,且
P(X=10)=0.8×0.9=0.72, P(X=5)=0.2×0.9=0.18,
P(X=2)=0.8×0.1=0.08, P(X=-3)=0.2×0.1=0.02。
由此得X的分布列为:
|
X |
10 |
5 |
2 |
-3 |
|
P |
0.72 |
0.18 |
0.08 |
0.02 |
(2)设生产的4件甲产品中一等品有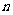 件,则二等品有
件,则二等品有 件。
件。
由题设知 ,解得
,解得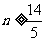 ,
,
又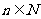 ,得
,得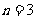 ,或
,或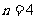 。
。
所求概率为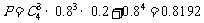
答:生产4件甲产品所获得的利润不少于10万元的概率为0.8192。
21. [选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
[选做题]本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答。若多做,则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。
A. 选修4-1:几何证明选讲
(本小题满分10分)
AB是圆O的直径,D为圆O上一点,过D作圆O的切线交AB延长线于点C,若DA=DC,求证:AB=2BC。
[解析] 本题主要考查三角形、圆的有关知识,考查推理论证能力。
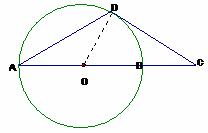 (方法一)证明:连结OD,则:OD⊥DC,
(方法一)证明:连结OD,则:OD⊥DC,
又OA=OD,DA=DC,所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=300,∠DOC=600,
所以OC=2OD,即OB=BC=OD=OA,所以AB=2BC。
(方法二)证明:连结OD、BD。
 因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为AB是圆O的直径,所以∠ADB=900,AB=2 OB。
因为DC 是圆O的切线,所以∠CDO=900。
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO。
即2OB=OB+BC,得OB=BC。
故AB=2BC。
B. 选修4-2:矩阵与变换
(本小题满分10分)
在平面直角坐标系xOy中,已知点A(0,0),B(-2,0),C(-2,1)。设k为非零实数,矩阵M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
[解析] 本题主要考查图形在矩阵对应的变换下的变化特点,考查运算求解能力。满分10分。
解:由题设得
由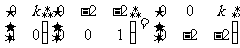 ,可知A1(0,0)、B1(0,-2)、C1(
,可知A1(0,0)、B1(0,-2)、C1(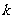 ,-2)。
,-2)。
计算得△ABC面积的面积是1,△A1B1C1的面积是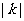 ,则由题设知:
,则由题设知: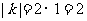 。
。
所以k的值为2或-2。
C. 选修4-4:坐标系与参数方程
(本小题满分10分)
在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值。
[解析] 本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力。满分10分。
解: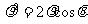 ,圆ρ=2cosθ的普通方程为:
,圆ρ=2cosθ的普通方程为: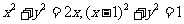 ,
,
直线3ρcosθ+4ρsinθ+a=0的普通方程为: ,
,
又圆与直线相切,所以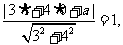 解得:
解得: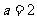 ,或
,或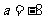 。
。
D. 选修4-5:不等式选讲
(本小题满分10分)
设a、b是非负实数,求证: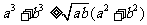 。
。
[解析] 本题主要考查证明不等式的基本方法,考查推理论证的能力。满分10分。
(方法一)证明: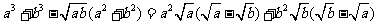
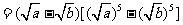
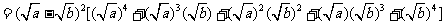
因为实数a、b≥0,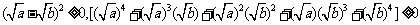
所以上式≥0。即有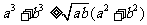 。
。
(方法二)证明:由a、b是非负实数,作差得
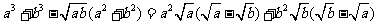
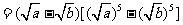
当 时,
时,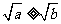 ,从而
,从而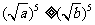 ,得
,得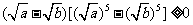 ;
;
当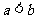 时,
时,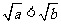 ,从而
,从而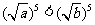 ,得
,得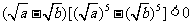 ;
;
所以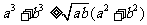 。
。
[必做题]第22题、第23题,每题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
20、(本小题满分16分)
设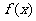 是定义在区间
是定义在区间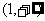 上的函数,其导函数为
上的函数,其导函数为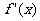 。如果存在实数
。如果存在实数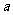 和函数
和函数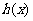 ,其中
,其中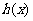 对任意的
对任意的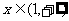 都有
都有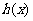 >0,使得
>0,使得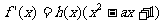 ,则称函数
,则称函数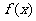 具有性质
具有性质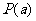 。
。
(1)设函数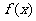
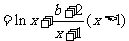 ,其中
,其中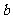 为实数。
为实数。
(i)求证:函数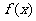 具有性质
具有性质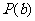 ; (ii)求函数
; (ii)求函数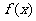 的单调区间。
的单调区间。
(2)已知函数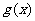 具有性质
具有性质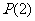 。给定
。给定 设
设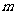 为实数,
为实数,
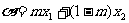 ,
,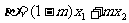 ,且
,且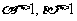 ,
,
若| |<|
|<| |,求
|,求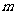 的取值范围。
的取值范围。
[解析] 本小题主要考查函数的概念、性质、图象及导数等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分。
(1)(i)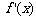
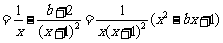
∵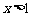 时,
时,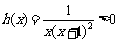 恒成立,
恒成立,
∴函数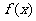 具有性质
具有性质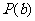 ;
;
(ii)(方法一)设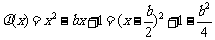 ,
,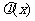 与
与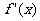 的符号相同。
的符号相同。
当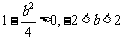 时,
时,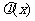
 ,
,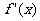
 ,故此时
,故此时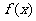 在区间
在区间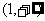 上递增;
上递增;
当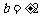 时,对于
时,对于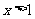 ,有
,有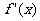
 ,所以此时
,所以此时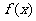 在区间
在区间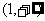 上递增;
上递增;
当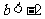 时,
时,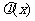 图像开口向上,对称轴
图像开口向上,对称轴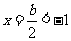 ,而
,而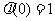 ,
,
对于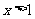 ,总有
,总有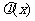
 ,
,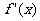
 ,故此时
,故此时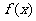 在区间
在区间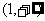 上递增;
上递增;
(方法二)当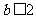 时,对于
时,对于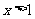 ,
,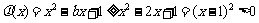
所以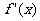
 ,故此时
,故此时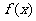 在区间
在区间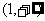 上递增;
上递增;
当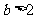 时,
时,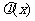 图像开口向上,对称轴
图像开口向上,对称轴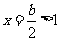 ,方程
,方程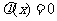 的两根为:
的两根为: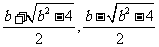 ,而
,而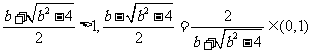
当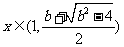 时,
时,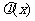
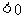 ,
,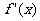
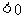 ,故此时
,故此时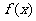 在区间
在区间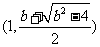 上递减;同理得:
上递减;同理得: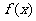 在区间
在区间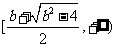 上递增。
上递增。
综上所述,当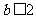 时,
时,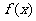 在区间
在区间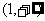 上递增;
上递增;
当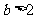 时,
时,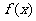 在
在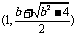 上递减;
上递减;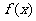 在
在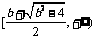 上递增。
上递增。
(2)(方法一)由题意,得: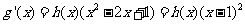
又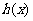 对任意的
对任意的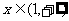 都有
都有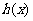 >0,
>0,
所以对任意的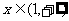 都有
都有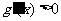 ,
,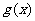 在
在 上递增。
上递增。
又 。
。
当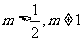 时,
时,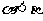 ,且
,且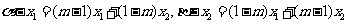 ,
,
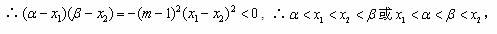
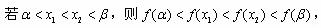
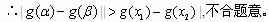
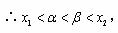

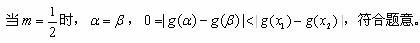
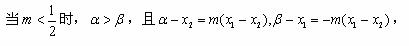
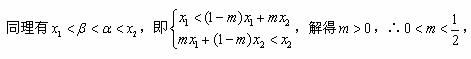
综合以上讨论,得:所求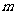 的取值范围是(0,1)。
的取值范围是(0,1)。
(方法二)由题设知,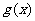 的导函数
的导函数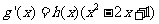 ,其中函数
,其中函数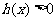 对于任意的
对于任意的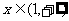 都成立。所以,当
都成立。所以,当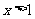 时,
时,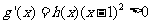 ,从而
,从而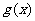 在区间
在区间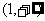 上单调递增。
上单调递增。
①当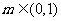 时,有
时,有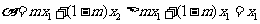 ,
,
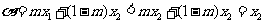 ,得
,得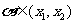 ,同理可得
,同理可得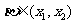 ,所以由
,所以由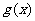 的单调性知
的单调性知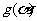 、
、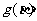
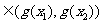 ,
,
从而有| |<|
|<| |,符合题设。
|,符合题设。
②当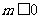 时,
时,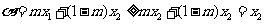 ,
,
 ,于是由
,于是由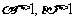 及
及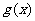 的单调性知
的单调性知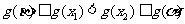 ,所以|
,所以| |≥|
|≥| |,与题设不符。
|,与题设不符。
③当 时,同理可得
时,同理可得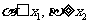 ,进而得|
,进而得| |≥|
|≥| |,与题设不符。
|,与题设不符。
因此综合①、②、③得所求的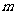 的取值范围是(0,1)。
的取值范围是(0,1)。
数学Ⅱ(附加题)
19、(本小题满分16分)
设各项均为正数的数列 的前n项和为
的前n项和为 ,已知
,已知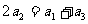 ,数列
,数列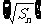 是公差为
是公差为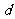 的等差数列。
的等差数列。
(1)求数列 的通项公式(用
的通项公式(用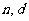 表示);
表示);
(2)设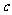 为实数,对满足
为实数,对满足 的任意正整数
的任意正整数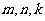 ,不等式
,不等式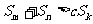 都成立。求证:
都成立。求证: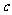 的最大值为
的最大值为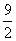 。
。
[解析] 本小题主要考查等差数列的通项、求和以及基本不等式等有关知识,考查探索、分析及论证的能力。满分16分。
(1)由题意知: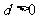 ,
,
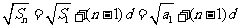
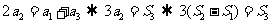 ,
,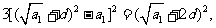
化简,得: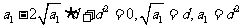
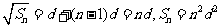 ,
,
当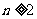 时,
时,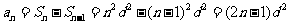 ,适合
,适合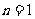 情形。
情形。
故所求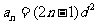
(2)(方法一)
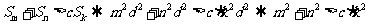 ,
, 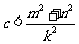 恒成立。
恒成立。
又 ,
,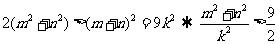 ,
,
故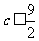 ,即
,即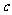 的最大值为
的最大值为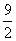 。
。
(方法二)由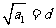 及
及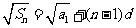 ,得
,得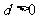 ,
,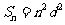 。
。
于是,对满足题设的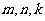 ,
,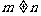 ,有
,有
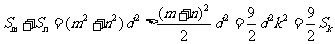 。
。
所以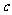 的最大值
的最大值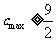 。
。
另一方面,任取实数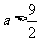 。设
。设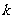 为偶数,令
为偶数,令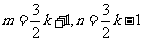 ,则
,则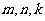 符合条件,且
符合条件,且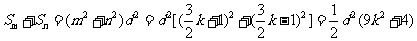 。
。
于是,只要 ,即当
,即当 时,
时,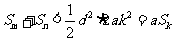 。
。
所以满足条件的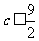 ,从而
,从而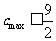 。
。
因此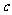 的最大值为
的最大值为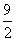 。
。
18、(本小题满分16分)
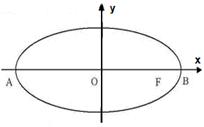 在平面直角坐标系
在平面直角坐标系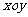 中,如图,已知椭圆
中,如图,已知椭圆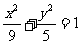 的左、右顶点为A、B,右焦点为F。设过点T(
的左、右顶点为A、B,右焦点为F。设过点T(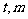 )的直线TA、TB与椭圆分别交于点M
)的直线TA、TB与椭圆分别交于点M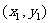 、
、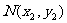 ,其中m>0,
,其中m>0,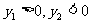 。
。
(1)设动点P满足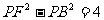 ,求点P的轨迹;
,求点P的轨迹;
(2)设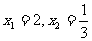 ,求点T的坐标;
,求点T的坐标;
(3)设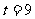 ,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
,求证:直线MN必过x轴上的一定点(其坐标与m无关)。
[解析] 本小题主要考查求简单曲线的方程,考查方直线与椭圆的方程等基础知识。考查运算求解能力和探究问题的能力。满分16分。
(1)设点P(x,y),则:F(2,0)、B(3,0)、A(-3,0)。
由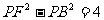 ,得
,得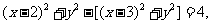 化简得
化简得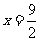 。
。
故所求点P的轨迹为直线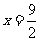 。
。
(2)将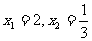 分别代入椭圆方程,以及
分别代入椭圆方程,以及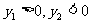 得:M(2,
得:M(2,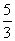 )、N(
)、N(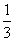 ,
,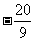 )
)
直线MTA方程为: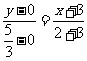 ,即
,即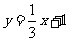 ,
,
直线NTB 方程为: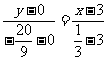 ,即
,即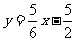 。
。
 联立方程组,解得:
联立方程组,解得: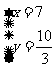 ,
,
所以点T的坐标为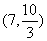 。
。
(3)点T的坐标为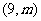
直线MTA方程为: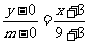 ,即
,即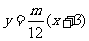 ,
,
直线NTB 方程为: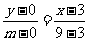 ,即
,即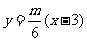 。
。
分别与椭圆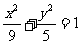 联立方程组,同时考虑到
联立方程组,同时考虑到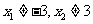 ,
,
解得: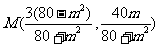 、
、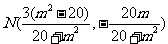 。
。
(方法一)当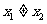 时,直线MN方程为:
时,直线MN方程为: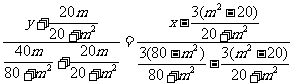
令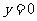 ,解得:
,解得: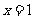 。此时必过点D(1,0);
。此时必过点D(1,0);
当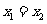 时,直线MN方程为:
时,直线MN方程为: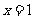 ,与x轴交点为D(1,0)。
,与x轴交点为D(1,0)。
所以直线MN必过x轴上的一定点D(1,0)。
(方法二)若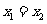 ,则由
,则由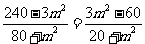 及
及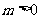 ,得
,得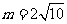 ,
,
此时直线MN的方程为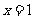 ,过点D(1,0)。
,过点D(1,0)。
若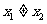 ,则
,则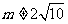 ,直线MD的斜率
,直线MD的斜率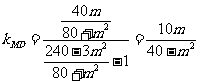 ,
,
直线ND的斜率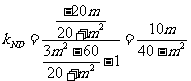 ,得
,得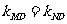 ,所以直线MN过D点。
,所以直线MN过D点。
因此,直线MN必过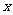 轴上的点(1,0)。
轴上的点(1,0)。
17、(本小题满分14分)
某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=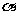 ,∠ADE=
,∠ADE=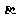 。
。
(1)该小组已经测得一组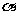 、
、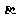 的值,tan
的值,tan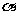 =1.24,tan
=1.24,tan =1.20,请据此算出H的值;
=1.20,请据此算出H的值;
(2)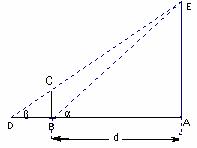 该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使
该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使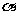 与
与 之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,
之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,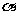 -
-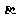 最大?
最大?
[解析] 本题主要考查解三角形的知识、两角差的正切及不等式的应用。
(1)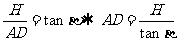 ,同理:
,同理: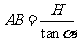 ,
,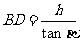 。
。
AD-AB=DB,故得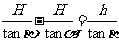 ,解得:
,解得: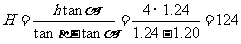 。
。
因此,算出的电视塔的高度H是124m。
(2)由题设知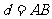 ,得
,得 ,
,

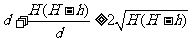 ,(当且仅当
,(当且仅当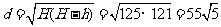 时,取等号)
时,取等号)
故当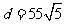 时,
时,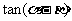 最大。
最大。
因为 ,则
,则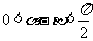 ,所以当
,所以当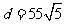 时,
时,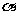 -
-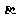 最大。
最大。
故所求的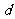 是
是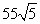 m。
m。
16、(本小题满分14分)
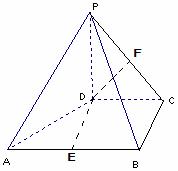
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
[解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查几何体的体积,考查空间想象能力、推理论证能力和运算能力。满分14分。
(1)证明:因为PD⊥平面ABCD,BC 平面ABCD,所以PD⊥BC。
平面ABCD,所以PD⊥BC。
由∠BCD=900,得CD⊥BC,
又PD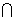 DC=D,PD、DC
DC=D,PD、DC 平面PCD,
平面PCD,
所以BC⊥平面PCD。
因为PC 平面PCD,故PC⊥BC。
平面PCD,故PC⊥BC。
 (2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
(2)(方法一)分别取AB、PC的中点E、F,连DE、DF,则:
易证DE∥CB,DE∥平面PBC,点D、E到平面PBC的距离相等。
又点A到平面PBC的距离等于E到平面PBC的距离的2倍。
由(1)知:BC⊥平面PCD,所以平面PBC⊥平面PCD于PC,
因为PD=DC,PF=FC,所以DF⊥PC,所以DF⊥平面PBC于F。
易知DF=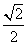 ,故点A到平面PBC的距离等于
,故点A到平面PBC的距离等于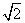 。
。
(方法二)体积法:连结AC。设点A到平面PBC的距离为h。
因为AB∥DC,∠BCD=900,所以∠ABC=900。
从而AB=2,BC=1,得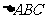 的面积
的面积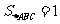 。
。
由PD⊥平面ABCD及PD=1,得三棱锥P-ABC的体积 。
。
因为PD⊥平面ABCD,DC 平面ABCD,所以PD⊥DC。
平面ABCD,所以PD⊥DC。
又PD=DC=1,所以 。
。
由PC⊥BC,BC=1,得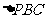 的面积
的面积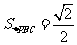 。
。
由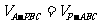 ,
,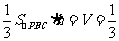 ,得
,得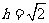 ,
,
故点A到平面PBC的距离等于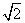 。
。
15、(本小题满分14分)
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1)。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(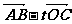 )·
)·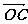 =0,求t的值。
=0,求t的值。
[解析]本小题考查平面向量的几何意义、线性运算、数量积,考查运算求解能力。满分14分。
(1)(方法一)由题设知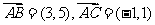 ,则
,则
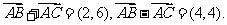
所以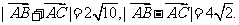
故所求的两条对角线的长分别为 、
、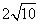 。
。
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC= 、AD=
、AD=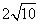 ;
;
(2)由题设知: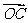 =(-2,-1),
=(-2,-1),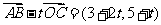 。
。
由(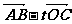 )·
)·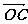 =0,得:
=0,得: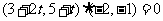 ,
,
从而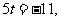 所以
所以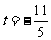 。
。
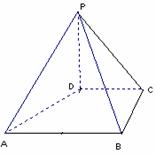 或者:
或者: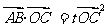 ,
,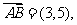
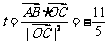
14、将边长为1m正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记 ,则S的最小值是____▲____。
,则S的最小值是____▲____。
[解析] 考查函数中的建模应用,等价转化思想。一题多解。
设剪成的小正三角形的边长为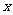 ,则:
,则:
(方法一)利用导数求函数最小值。
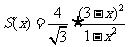 ,
,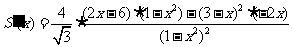

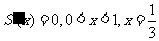 ,
,
当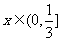 时,
时,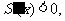 递减;当
递减;当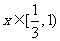 时,
时,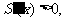 递增;
递增;
故当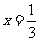 时,S的最小值是
时,S的最小值是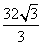 。
。
(方法二)利用函数的方法求最小值。
令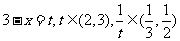 ,则:
,则: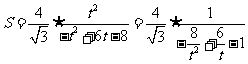
故当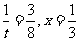 时,S的最小值是
时,S的最小值是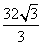 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com