
2.当天太阳直射点的位置和移动方向是
A.南半球,向北移 B.北半球,向北移
C.北半球,向南移 D.南半球,向南移
世博会期间,上海城市中心地区基本建成以地铁、地下道路、地下人行公共步道、地下停车设施为主的地下交通系统,地铁将承担60%以上的城市客运交通。据此完成第3题。
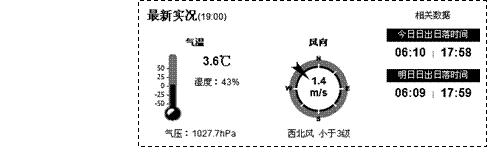
1.据图中所示信息,与当日最接近的节气是
A.秋分(9月23日) B.寒露(10月8日)
C.春分(3月21日) D.清明(4月5日)
3.第Ⅰ卷共35小题,每小题4分,共140分。在每题给出的四个选项中,只有一项
是符合题目要求的。\
下图为天气网上海某日天气预报的截图。据此完成1-2题。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,
用橡皮擦干净后,再选涂其他答案标号。在试题卷上作答无效。
24.(本题满分10分)已知关于 的不等式
的不等式 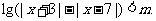
(1)当 时,解此不等式;
时,解此不等式;
(2)设函数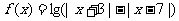 ,当
,当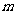 为何值时,
为何值时,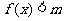 恒成立?
恒成立?

 2009-2010学年“拼搏一年·成就梦想”
2009-2010学年“拼搏一年·成就梦想”
23.(本题满分10分)知在平面直角坐标系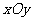 内,点
内,点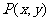 在曲线C:
在曲线C: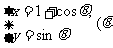 为参数,
为参数,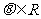 )上运动.以
)上运动.以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线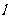 的极坐标方程为
的极坐标方程为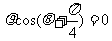 .
.
(1)写出曲线C的标准方程和直线 的直角坐标方程;
的直角坐标方程;
(2)若直线 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求 面积的最大值.
面积的最大值.
22.(本题满分10分)如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC、MB、OT.
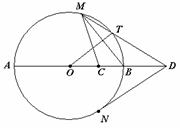 (1)求证:
(1)求证: ;
;
(2)若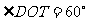 ,试求
,试求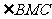 的大小.
的大小.
21.(本题满分12分)已知圆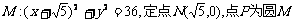 上的动点,
上的动点,
点Q在NP上,点G在MP上,且满足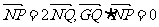 .
.
(1)求点G的轨迹C的方程;
(2)过点(2,0)作直线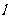 ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设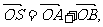 是否存在这样的直线
是否存在这样的直线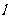 ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线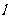 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
请在下面三题中任选一题做答,如果多做,则按所做的第一题记分.
20.(本题满分12分)设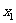 、
、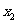
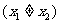 是函数
是函数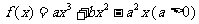 的两个
的两个
极值点.
(1)若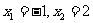 ,求函数
,求函数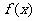 的解析式;
的解析式;
(2)若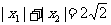 ,求
,求 的最大值.
的最大值.
19.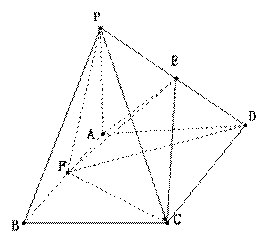 (本题满分12分)已知:四棱锥
(本题满分12分)已知:四棱锥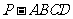 中,
中,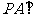 平面
平面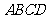 , 底面
, 底面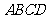 是菱形, 且
是菱形, 且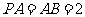 ,
, 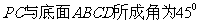 ,
,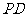 的中点为
的中点为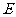 ,
,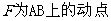 .
.
(1)求三棱锥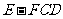 的体积;
的体积;
(2)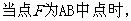 试判断
试判断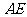 与平面
与平面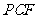 的位
的位
置关系,并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com