
3.钱永健先生因在研究绿色荧光蛋白方面的杰出成就而获2008年诺贝尔奖。在某种生物中检测不到绿色荧光,将水母绿色荧光蛋白基因转入该生物体内后,结果可以检测到绿色荧光。由此可知
A.该生物的基因型是杂合的
B.该生物与水母有很近的亲缘关系
C.绿色荧光蛋白基因在该生物体内得到了表达
D.改变绿色荧光蛋白基因的1个核苷酸对,就不能检测到绿色荧光
2.对基因表达载体构建的一些说法,不正确的是
A.需要限制酶和DNA连接酶参与 B.基因表达载体中含有启动子和密码子
C.通常用抗生素基因作为标记基因 D.基因表达载体的构建是基因工程的核心
1.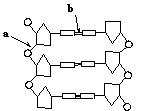 依右图有关工具酶功能的叙述,不正确的是
依右图有关工具酶功能的叙述,不正确的是
A.切断a处的酶为限制性内切酶
B.连接a处的酶为DNA连接酶
C.切断b处的酶为解旋酶
D.连接b处的酶为RNA聚合酶
16.(2010湖南文数) (本小题满分12分)
已知函数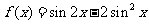
(I)求函数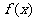 的最小正周期。
的最小正周期。
(II) 求函数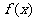 的最大值及
的最大值及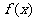 取最大值时x的集合。
取最大值时x的集合。

(2010浙江理数)(18)(本题满分l4分)在△ABC中,角A、B、C所对的边分别为a,b,c,已知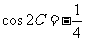
(I)求sinC的值;
(Ⅱ)当a=2, 2sinA=sinC时,求b及c的长.
解析:本题主要考察三角变换、正弦定理、余弦定理等基础知识,同事考查运算求解能力。
(Ⅰ)解:因为cos2C=1-2sin2C=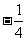 ,及0<C<π
,及0<C<π
所以sinC=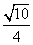 .
.
(Ⅱ)解:当a=2,2sinA=sinC时,由正弦定理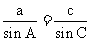 ,得
,得
c=4
由cos2C=2cos2C-1= ,J及0<C<π得
,J及0<C<π得
cosC=±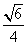
由余弦定理c2=a2+b2-2abcosC,得
b2±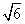 b-12=0
b-12=0
解得 b=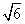 或2
或2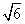

 所以 b=
所以 b=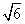 b=
b=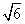
c=4 或 c=4
(2010全国卷2理数)(17)(本小题满分10分)
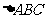 中,
中,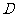 为边
为边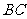 上的一点,
上的一点, ,
,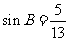 ,
,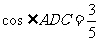 ,求
,求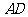 .
.
[命题意图]本试题主要考查同角三角函数关系、两角和差公式和正弦定理在解三角形中的应用,考查考生对基础知识、基本技能的掌握情况.
19.(2010上海文数)(本题满分12分)
已知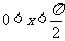 ,化简:
,化简:
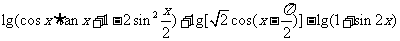 .
.
解析:原式=lg(sinx+cosx)+lg(cosx+sinx)-lg(sinx+cosx)2=0.
3.(2010江苏卷)13、在锐角三角形ABC,A、B、C的对边分别为a、b、c,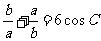 ,则
,则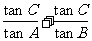 =____▲_____。
=____▲_____。
[解析] 考查三角形中的正、余弦定理三角函数知识的应用,等价转化思想。一题多解。
(方法一)考虑已知条件和所求结论对于角A、B和边a、b具有轮换性。
当A=B或a=b时满足题意,此时有: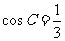 ,
,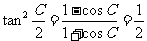 ,
,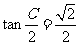 ,
,
 ,
,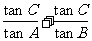 = 4。
= 4。
(方法二)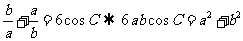 ,
,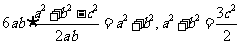
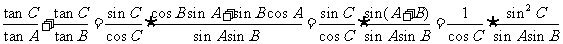
2010年高考数学试题分类汇编--三角函数
2.(2010江苏卷)10、定义在区间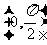 上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
上的函数y=6cosx的图像与y=5tanx的图像的交点为P,过点P作PP1⊥x轴于点P1,直线PP1与y=sinx的图像交于点P2,则线段P1P2的长为_______▲_____。
[解析] 考查三角函数的图象、数形结合思想。线段P1P2的长即为sinx的值,
且其中的x满足6cosx=5tanx,解得sinx=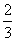 。线段P1P2的长为
。线段P1P2的长为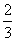
1. (2010福建理数)14.已知函数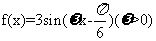 和
和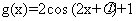 的图象的对称轴完全相同。若
的图象的对称轴完全相同。若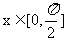 ,则
,则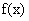 的取值范围是
。
的取值范围是
。
[答案]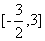
[解析]由题意知, ,因为
,因为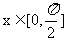 ,所以
,所以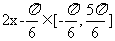 ,由三角函数图象知:
,由三角函数图象知:
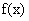 的最小值为
的最小值为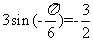 ,最大值为
,最大值为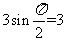 ,所以
,所以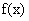 的取值范围是
的取值范围是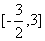 。
。
14.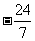 [命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[命题意图]本小题主要考查三角函数值符号的判断、同角三角函数关系、和角的正切公式,同时考查了基本运算能力及等价变换的解题技能.
[解析]因为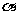 为第二象限的角,又
为第二象限的角,又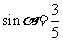 , 所以
, 所以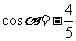 ,
,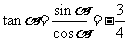 ,所
,所
(2010全国卷1理数)(14)已知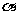 为第三象限的角,
为第三象限的角,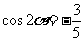 ,则
,则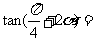 .
.

(2010山东理数)

16.(2010福建文数)观察下列等式:K^S*5U.C#O
① cos2a=2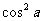 -1;
-1;
② cos4a=8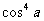 - 8
- 8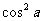 + 1;
+ 1;
③ cos6a=32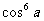 - 48
- 48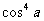 + 18
+ 18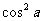 - 1;
- 1;
④ cos8a=128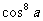 - 256
- 256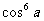 + 160
+ 160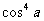 - 32
- 32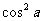 + 1;
+ 1;
⑤ cos10a= m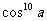 - 1280
- 1280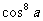 + 1120
+ 1120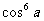 + n
+ n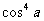 + p
+ p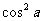 - 1.
- 1.
可以推测,m – n + p = .
[答案]962
[解析]因为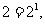
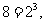
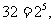
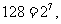 所以
所以 ;观察可得
;观察可得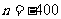 ,
,
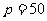 ,所以m – n + p =962。
,所以m – n + p =962。
[命题意图]本小题考查三角变换、类比推理等基础知识,考查同学们的推理能力等。
(2010全国卷1文数)(14)已知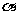 为第二象限的角,
为第二象限的角,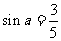 ,则
,则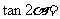 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com