2．汽车以20 m/s的速度做匀速直线运动，刹车后的加速度为5 m/s2，那么开始刹车后2 s与开始刹车后6 s汽车通过的位移之比为

A．1∶4　　　　　　　　　　　 B.3∶5　　　　　　　　　 C.3∶4　　　　　　　　　　　　 D.5∶9

1．骑自行车的人沿着直线从静止开始运动，运动后，在第1 s、2 s、3 s、4 s内，通过的路程分别为1 m、2 m、3 m、4 m，有关其运动的描述正确的是

A．4 s内的平均速度是2.5 m/s

B．在第3、4 s内平均速度是3.5 m/s

C．第3 s末的即时速度一定是3 m/s

D．该运动一定是匀加速直线运动

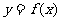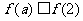6.函数是R上的偶函数，且在上是增函数，若,则实数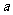的取值范围是 　　　　　

[学后反思]____________________________________________________ _______

　　　　　 _____________________________________________________________

　　 　　　_____________________________________________________________

5.若函数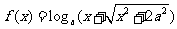是奇函数，则____________________

4.函数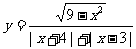的图象关于　　　　　　　　 对称　

3.已知函数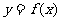为奇函数，若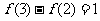，则　　 ．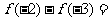

2.设函数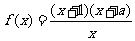为奇函数，则________________．

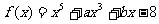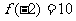1.已知且，那么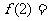　　　　　

2．与函数周期有关的结论：

①已知条件中如果出现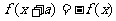、或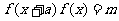(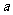、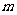均为非零常数，)，都可以得出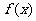的周期为　　 　　　；

②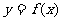的图象关于点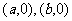中心对称或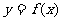的图象关于直线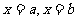轴对称，均可以得到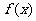周期　　　　　　　　　

　[典型例析]

例1.　 判断下列函数的奇偶性.

(1)f(x)=;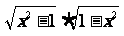

(2)f(x)=log₂(x+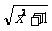) (x∈R);

(3)f(x)=lg|x-2|.　

变式训练1：判断下列各函数的奇偶性：

(1)f(x)=(x-2)；　

(2)f(x)=；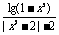

(3)f(x)=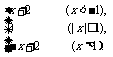

小结：

例2　 已知f(x)是R上的奇函数，且当x∈(-∞,0)时，f(x)=-xlg(2-x),求f(x)的解析式.

变式训练2：已知函数f(x)的定义域为R，且满足f(x+2)=-f(x)

(1)求证：f(x)是周期函数；

(2)若f(x)为奇函数，且当0≤x≤1时，f(x)=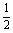x,求f(x)[-1,1] 的解析式。

思考(1，3)上的解析式怎么求？

例3已知函数f(x)=x²+|x-a|+1,a∈R.

(1)试判断f(x)的奇偶性；

(2)若-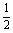≤a≤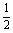，求f(x)的最小值.

[当堂检测]

1．奇偶性：

① 定义：如果对于函数f (x)定义域内的任意x都有　　　　　 ，则称f (x)为奇函

数；若　　　　　　 ，则称f (x)为偶函数.　 如果函数f (x)不具有上述性质，则f (x)

不具有　　　 　　　. 如果函数同时具有上述两条性质，则f(x)　　　　　 .

② 简单性质：

1) 图象的对称性质：一个函数是奇函数的充要条件是它的图象关于　　　 对称；一个函数是偶函数的充要条件是它的图象关于　　　 对称.

2) 函数f(x)具有奇偶性的必要条件是其定义域关于　　　　 对称.

3)奇函数f(x)在定义域内，对称区间上单调性有什么特点？___________________

偶函数又有怎样的特点？____________________

4)奇函数在对称区间上最值有怎样的特点？___________________________________

偶函数在对称区间上最值又有怎样的特点____________________________________

5) 你能举一个既是奇函数也是偶函数的函数吗？______________________________

这样的函数有什么的特点？_____________________________________________

6)函数奇偶性与单调性有什么联系与区别？

　 ________________________________________________________________________