
19.(本小题共13分)
在平面直角坐标系xOy中,经过点(0, 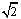 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆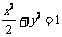 有两个不同的交点P和Q.
有两个不同的交点P和Q.
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量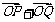 与
与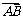 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
 由此可解得
由此可解得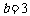 .………………………………………………………… 5分
.………………………………………………………… 5分
∵ b>2a , 且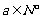 , ∴
, ∴ 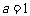 ,从而c =-2.
,从而c =-2.
∴ 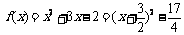 .
.
即 f(x)的最小值为 .………………………………………………… 7分
.………………………………………………… 7分
(Ⅱ) 令x =1,代入 得
得
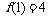 ,即
,即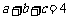 .
.
从而 .
又由
.
又由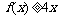 ,得
,得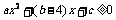 .
.
因a > 0,
故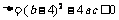 .
.
即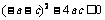 ,
, 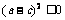 . 从而
. 从而 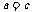 .…………………… 10分
.…………………… 10分
∵ 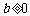 ,∴
,∴
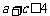 ,
,
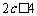 .
.
又 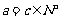 , ∴ c =1或c =2.………………………………………… 12分
, ∴ c =1或c =2.………………………………………… 12分
当c =2时,b=0, 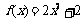 .此时
.此时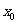 不满足
不满足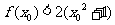 .
.
故c =2不符合题意,舍去.
所以 c =1. ……………………………………………………………… 14分
∴ 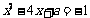 有且只有一个实数根.
有且只有一个实数根.
∴ 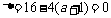 . ∴
. ∴
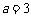 .………………………………… 4分
.………………………………… 4分
∴ 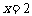 ,
,  .
.
∴ 切线l: 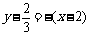 . 即
. 即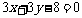 .……………………… 7分
.……………………… 7分
(Ⅱ) ∵  .……………………………… 9分
.……………………………… 9分
∴ 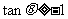 . ……………………………………………………… 10分
. ……………………………………………………… 10分
∵ 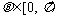 , ∴
, ∴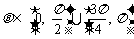 ……………………………
13分
……………………………
13分
17.(本小题共13分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和BC边上的点,且满足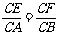 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由 ;
 当
当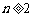 时,
时, 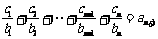 ,
, 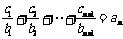 ,
,
两式相减,得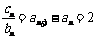 .
.
∴ 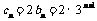 (
(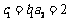 适合).……………………………… 11分
适合).……………………………… 11分
∴ 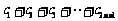
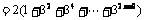
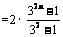
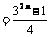 .
.
即 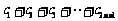
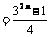 . ……………………………………… 14分
. ……………………………………… 14分
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率.
已知函数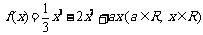 ,在曲线
,在曲线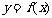 的所有切线中,有且仅有一条切线l与直线
的所有切线中,有且仅有一条切线l与直线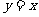 垂直.
垂直.
(Ⅰ)求a的值和切线l的方程;
(Ⅱ)设曲线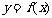 上任一点处的切线的倾斜角为
上任一点处的切线的倾斜角为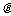 ,求
,求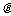 的取值范围.
的取值范围.
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,E、F分别是AC和
BC边上的点,且满足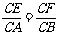 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由 ;
(Ⅱ) 求二面角B-AC-D的平面角的正切值.
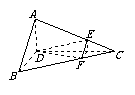
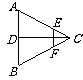
图(1) 图(2)
已知函数 ,数列
,数列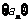 是公差为d的等差数列,
是公差为d的等差数列,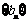 是公比为q
是公比为q
(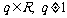 )的等比数列.若
)的等比数列.若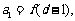
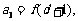
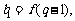
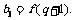
(Ⅰ)求数列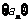 ,
,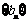 的通项公式;
的通项公式;
(Ⅱ)设数列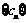 对任意自然数n均有
对任意自然数n均有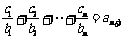 ,求
,求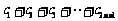 的值.
的值.
在平面直角坐标系xOy中,经过点(0, 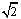 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆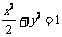 有两个不同的交点P和Q.
有两个不同的交点P和Q.
(Ⅰ)求k的取值范围;
(Ⅱ)设椭圆与x轴正半轴、y轴正半轴的交点分别为A,B,是否存在常数k,使得向量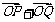 与
与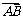 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由.
已知函数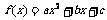 ,其中
,其中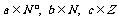 .
.
(Ⅰ)若b>2a,且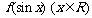 的最大值为2,最小值为-4,试求函数f(x)的最小值;
的最大值为2,最小值为-4,试求函数f(x)的最小值;
(Ⅱ)若对任意实数x,不等式 恒成立,且存在
恒成立,且存在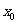 使得
使得 成立,求c的值.
成立,求c的值.
数学(文科)答案及评分参考
14. 设坐标平面内有一个质点从原点出发,沿x轴跳动,每次向正方向或负方向跳1个单位,若经过5次跳动质点落在点(3,0)处(允许重复过此点),则质点不同的运动方法共有___________种(用数字作答);若经过20次跳动质点落在点(16,0)处(允许重复过此点),则质点不同的运动方法共有___________种(用数字作答).
13. 函数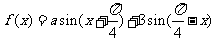 是偶函数,则a =_______________.
是偶函数,则a =_______________.
12. 过双曲线M: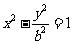 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线相交于B、C, 且
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线相交于B、C, 且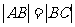 , 则双曲线M的离心率为_____________.
, 则双曲线M的离心率为_____________.
11. 若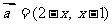 ,
,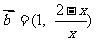 ,则使不等式
,则使不等式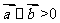 成立的x的取值范围是_________________________.
成立的x的取值范围是_________________________.
10. 若函数y=f(x)的图象与函数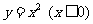 的图象关于直线x-y=0对称,则f(x)=
的图象关于直线x-y=0对称,则f(x)=
__________________________________.
9. 函数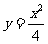 在点P(2, 1)处的切线方程为__________________________.
在点P(2, 1)处的切线方程为__________________________.
8.
设集合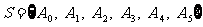 ,在S上定义运算“⊕”为:
,在S上定义运算“⊕”为: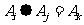 ,其中k为i + j被4除的余数 ,
,其中k为i + j被4除的余数 , 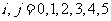 .则满足关系式
.则满足关系式 的
的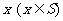 的个数为
的个数为
(A)1 (B)2
(C)3 (D)4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com