
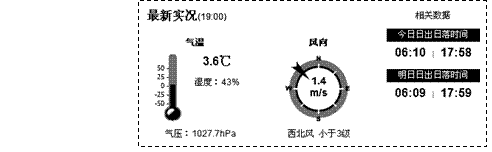
1.据图中所示信息,与当日最接近的节气是
A.秋分(9月23日) B.寒露(10月8日)
C.春分(3月21日) D.清明(4月5日)
3.第Ⅰ卷共35小题,每小题4分,共140分。在每题给出的四个选项中,只有一项
是符合题目要求的。\
下图为天气网上海某日天气预报的截图。据此完成1-2题。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,
用橡皮擦干净后,再选涂其他答案标号。在试题卷上作答无效。
24.(本题满分10分)已知关于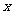 的不等式
的不等式 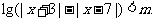
(1)当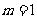 时,解此不等式;
时,解此不等式;
(2)设函数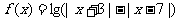 ,当
,当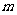 为何值时,
为何值时, 恒成立?
恒成立?

 2009-2010学年“拼搏一年·成就梦想”
2009-2010学年“拼搏一年·成就梦想”
23.(本题满分10分)知在平面直角坐标系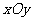 内,点
内,点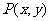 在曲线C:
在曲线C: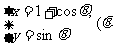 为参数,
为参数,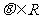 )上运动.以
)上运动.以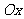 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线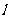 的极坐标方程为
的极坐标方程为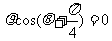 .
.
(1)写出曲线C的标准方程和直线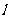 的直角坐标方程;
的直角坐标方程;
(2)若直线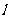 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求 面积的最大值.
面积的最大值.
22.(本题满分10分)如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC、MB、OT.
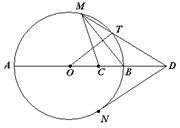 (1)求证:
(1)求证: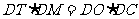 ;
;
(2)若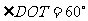 ,试求
,试求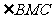 的大小.
的大小.
21.(本题满分12分)已知圆 上的动点,
上的动点,
点Q在NP上,点G在MP上,且满足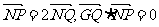 .
.
(1)求点G的轨迹C的方程;
(2)过点(2,0)作直线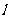 ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设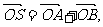 是否存在这样的直线
是否存在这样的直线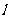 ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线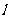 的方程;若不存在,试说明理由.
的方程;若不存在,试说明理由.
请在下面三题中任选一题做答,如果多做,则按所做的第一题记分.
20.(本题满分12分)设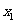 、
、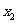
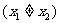 是函数
是函数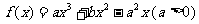 的两个
的两个
极值点.
(1)若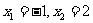 ,求函数
,求函数 的解析式;
的解析式;
(2)若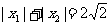 ,求
,求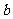 的最大值.
的最大值.
19.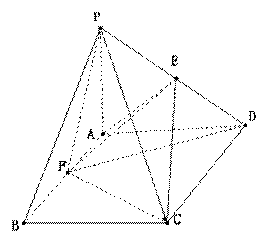 (本题满分12分)已知:四棱锥
(本题满分12分)已知:四棱锥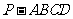 中,
中,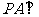 平面
平面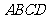 , 底面
, 底面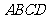 是菱形, 且
是菱形, 且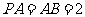 ,
, 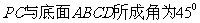 ,
,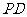 的中点为
的中点为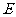 ,
,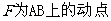 .
.
(1)求三棱锥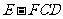 的体积;
的体积;
(2)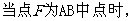 试判断
试判断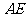 与平面
与平面 的位
的位
置关系,并说明理由.
18.(本题满分12分)某电视机生产厂家今年推出A、B、C、D四种款式电视机,每种款
式电视机的外观均有黑色、银白色两种. 四月份的电视机产量如下表(单位:台):
|
|
款式A |
款式B |
款式C |
款式D |
|
黑 色 |
150 |
200 |
200 |
x |
|
银白色 |
160 |
180 |
200 |
150 |
若按电视机的款式采取分层抽样的方法在这个月生产的电视机中抽取70台,其中有C种款式的电视机20台.
(1)求x的值.
(2)若在C种款式电视机中按颜色进行分层抽样抽取一个容量为6的样本,然后将该样本看成一个总体,从中任取2台,求恰有1台黑色、1台银白色电视机的概率.
(3)用简单随机抽样的方法从A种款式电视机中抽取10台,对其进行检测,它们的得分如下:94,92, 92,96,97,95, 98,90,94,97. 如果把这10台电视机的得分看作一个样本,从中任取一个数,求该数与样本平均数之差的绝对值不超过2的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com