
24.解:原不等式等价于
(Ⅰ)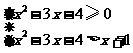 或(Ⅱ)
或(Ⅱ)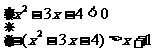 。。。。。。。。。。。。。4分
。。。。。。。。。。。。。4分
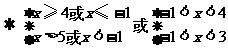
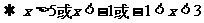
∴ 原不等式的解集为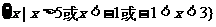 .。。。。。。。。。。。。。。。10分
.。。。。。。。。。。。。。。。10分
|

|
版权所有:()
版权所有:()
23.23.解:圆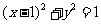 的极坐标方程为
的极坐标方程为 。。。。。。。。。。。。4分
。。。。。。。。。。。。4分
设点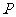 的极坐标为
的极坐标为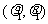 ,点
,点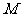 的极坐标为
的极坐标为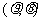 ,
,
∵点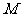 为线段
为线段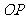 的中点, ∴
的中点, ∴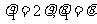 ,。。。。。。。。。。。7分
,。。。。。。。。。。。7分
将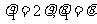 代入圆的极坐标方程,得
代入圆的极坐标方程,得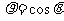 .
.
∴点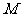 轨迹的极坐标方程为
轨迹的极坐标方程为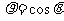 ,它表示圆心在点
,它表示圆心在点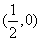 ,半径为
,半径为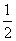 的圆.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10分
的圆.。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10分
23.证明:(1) ∵四边形ABCD是等腰梯形,∴AC=DB
∵AB=DC,BC=CB,∴△ABC≌△BCD。。。。。。。。。。。。。。。。。。。。5分
(2)∵△ABC≌△BCD,∴∠ACB=∠DBC,∠ABC=∠DCB
∵AD∥BC,∴∠DAC=∠ACB,∠EAD=∠ABC。。。。。。。。。。。。。8分
∵ED∥AC,∴∠EDA=∠DAC ∴∠EDA=∠DBC,∠EAD=∠DCB
∴△ADE∽△CBD ∴DE:BD=AE:CD, ∴DE·DC=AE·BD.。。。。。。。10分
21.解:(1)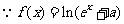 是实数集
是实数集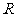 上的奇函数
上的奇函数
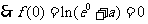
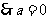 。。。。。。。。。。。。。。。。。。。。。。。。。3分
。。。。。。。。。。。。。。。。。。。。。。。。。3分
(2)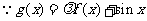 是区间
是区间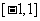 上的减函数
上的减函数 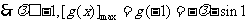
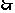 只需
只需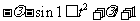
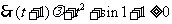 ,(
,( )恒成立。。。。5分
)恒成立。。。。5分
令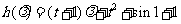 ,(
,( ) 则
) 则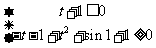
 ,而
,而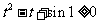 恒成立,
恒成立,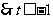 。。。。。。。。。。。7分
。。。。。。。。。。。7分
(3)由(1)知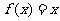
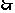 方程
方程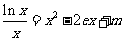
令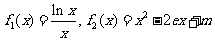
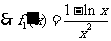 。。。8分
。。。8分
当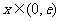 时,
时,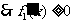 ,
,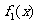 在
在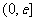 上是增函数
上是增函数
当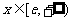 时,
时,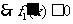 ,
,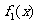 在
在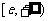 上是减函数
上是减函数
当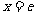 时,
时,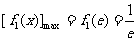 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9分
而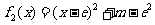
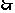 当
当 ,即
,即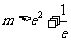 时,方程无解;。。。。。。。。。。。10分
时,方程无解;。。。。。。。。。。。10分
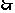 当
当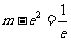 ,即
,即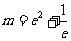 时,方程有一个根;。。。。。。。。。。。11分
时,方程有一个根;。。。。。。。。。。。11分
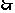 当
当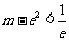 ,即
,即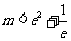 时,方程有两个根;。。。。。。。。。。。12分
时,方程有两个根;。。。。。。。。。。。12分
20.解:(1)
 ……………2分
……………2分
 ,渐近线方程为
,渐近线方程为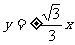 ………… 3分
………… 3分
(2)设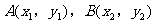 ,AB的中点
,AB的中点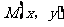
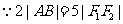
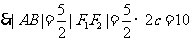

 ,
,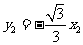 ,
,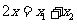 ,
,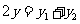 …………5分
…………5分
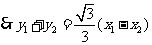 ,
,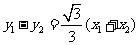
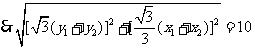
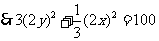 ,即
,即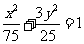 。。。。。。。。。。7分
。。。。。。。。。。7分
则M的轨迹是中心在原点,焦点在x轴上,长轴长为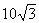 ,短轴长为
,短轴长为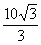 的椭圆.
的椭圆.
(3)假设存在满足条件的直线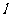
设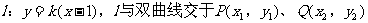
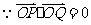 ,
, ,
,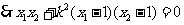
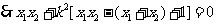 。。。。。。10分
。。。。。。10分
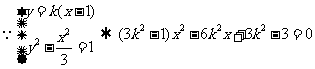 ,
,
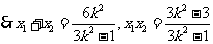 。。。。。。。。。。11分
。。。。。。。。。。11分
∴ ∴k不存在,即不存在满足条件的直线
∴k不存在,即不存在满足条件的直线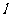 .。。。。。。。12分
.。。。。。。。12分
19.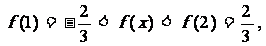 解: (Ⅰ)∵
解: (Ⅰ)∵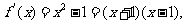
∴当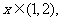
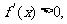
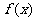 为增函数,
为增函数,
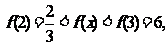 ∴
∴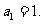 。。。2分
。。。2分
同理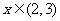 时,
时,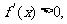
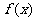 为增函数,
为增函数,
∴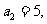 ∴
∴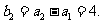 。。。。。。。。。。。。。。。。。。。。。。。3分
。。。。。。。。。。。。。。。。。。。。。。。3分
又∵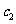 表示满足
表示满足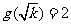 的正整数
的正整数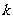 的个数.
的个数.
∴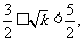 ∴
∴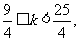
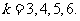 ∴
∴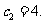 。。。。。。。。。4分
。。。。。。。。。4分
(Ⅱ)当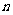 为正整数,且
为正整数,且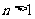 ,
,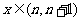 时,
时,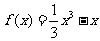 为增函数,
为增函数,
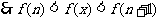
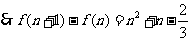
 。。。。 5分
。。。。 5分
∴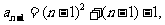
 。。6分
。。6分
又∵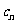 表示满足
表示满足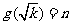 的正整数
的正整数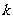 的个数,
的个数,
∴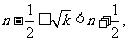 ∴
∴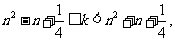
∴ 共
共 个.
个.
∴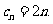 ∴
∴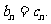 。。。。。。。。。8分
。。。。。。。。。8分
(Ⅲ)由(Ⅱ)知: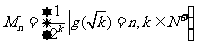
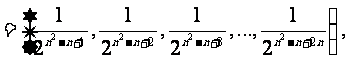
∴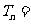

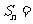

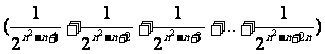
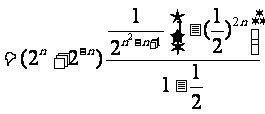 =
=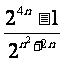
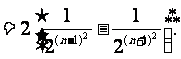 。。。。。10分
。。。。。10分
∴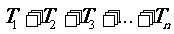
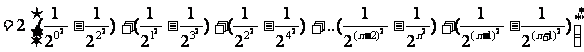
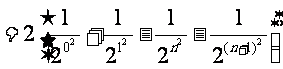
 。。。。。。。。12分
。。。。。。。。12分
(Ⅰ)∵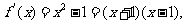
∴当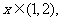
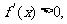
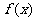 为增函数, 1分
为增函数, 1分
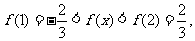 ∴
∴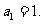 2分
2分
同理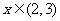 时,
时,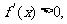
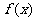 为增函数,
为增函数, 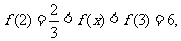 ∴
∴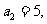 3分
3分
∴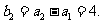
又∵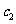 表示满足
表示满足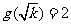 的正整数
的正整数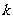 的个数.∴
的个数.∴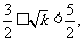 ∴
∴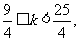
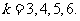
∴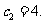
(Ⅱ)当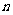 为正整数,且
为正整数,且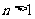 ,
,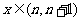 时,
时,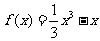 为增函数,
为增函数,

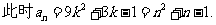
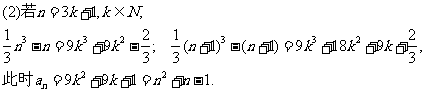
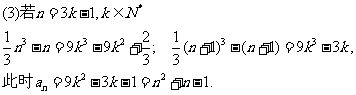
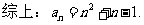 ∴
∴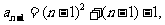
 9分
9分
又∵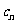 表示满足
表示满足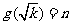 的正整数
的正整数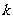 的个数,
的个数,
∴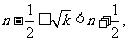 ∴
∴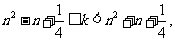
∴ 共
共 个. 11分
个. 11分
∴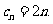 ∴
∴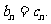 12分
12分
(Ⅲ)由(2)知: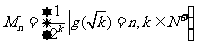
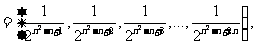
∴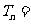

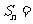

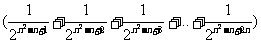
 =
=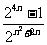
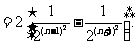
∴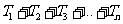
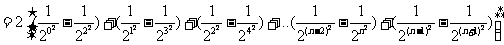
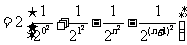
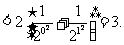
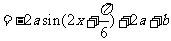 。。。。。。。。。。。。。。。。。。。。。。。2分
。。。。。。。。。。。。。。。。。。。。。。。2分
当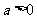 时,由
时,由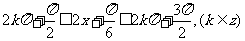 ,得
,得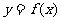 的单调递增区间为
的单调递增区间为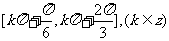 。。。。。。。。。。。。。。。。。。。。。。。。。4分
。。。。。。。。。。。。。。。。。。。。。。。。。4分
当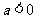 时,
时,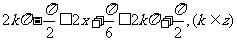 ,得
,得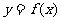 的单调递增区间
的单调递增区间
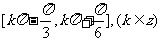 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
(2)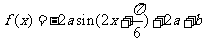 ,
,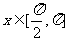 ,
,
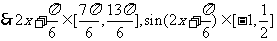 。。。。。。。。。。。。。。。。。。。8分
。。。。。。。。。。。。。。。。。。。8分
当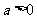 时,
时,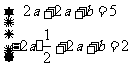 ,解得
,解得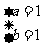 ,不满足
,不满足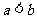 ,舍去。。。。。10分
,舍去。。。。。10分
当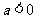 时,
时, ,解得
,解得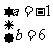 ,符合条件,
,符合条件,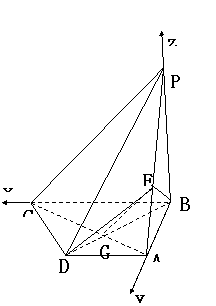 综上,
综上,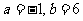 。。12分
。。12分
18.解:(1)建立如图所示的直角坐标系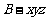 .
.
设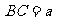 ,则
,则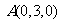 ,
,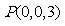 ,
,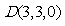 ,
,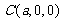 ,
,
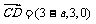 ,
,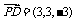 ,
,
∵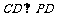 ,∴
,∴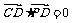 ,即
,即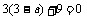 .∴
.∴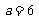 .……2分
.……2分
∵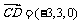 ,
,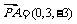 ,∴
,∴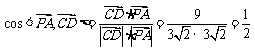 .
.
∴异面直线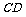 与
与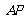 所成的角为
所成的角为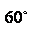 .……4分
.……4分
(2)连结AC交BD于G,连结EG.∴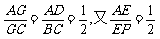 ∴
∴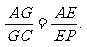 ……5分
……5分
∴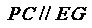 ……6分
……6分 ∴
∴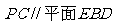 ……8分
……8分
(3)设平面 的法向量为
的法向量为
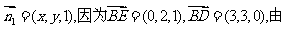
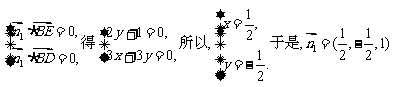 ……10分
……10分
又因为平面ABE的法向量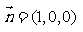
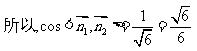 .
.
所以,二面角A-BE-D的大小为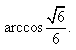 ……12分
……12分
24、(本小题满分10分)选修4-5:不等式选讲
解不等式 .
.
高三上学期期末数学复习题(二)答案
23、(本小题满分10分)选修4-4:坐标系与参数方程
设过原点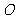 的直线与圆C:
的直线与圆C: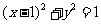 的一个交点为
的一个交点为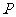 ,点
,点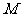 为线段
为线段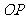 的中点。
的中点。
(1)求圆C的极坐标方程
(2)求点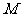 轨迹的极坐标方程,并说明它是什么曲线.
轨迹的极坐标方程,并说明它是什么曲线.
22、(本小题满分10分)选修4-1:几何证明选讲
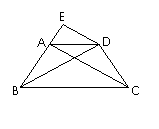 已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作
已知:如右图,在等腰梯形ABCD中,AD∥BC,AB=DC,过点D作
AC的平行线DE,交BA的延长线于点E.
求证:(1)△ABC≌△DCB
(2)DE·DC=AE·BD.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com