
22.(本小题满分10分) 选修4-1:几何证明选讲
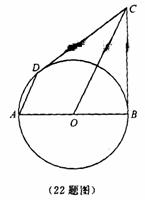 已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD。
已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD。
(1)求证:DC是⊙O的切线;
(2)设AB=2R,求证:AD·OC=2R2。
20.(本小题满分12分)
已知椭圆的中心在坐标原点O,焦点在x轴上,斜率为-1且过椭圆右焦点F的直线交椭圆于A、B两点,且直线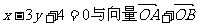 的基线共线。
的基线共线。
(I)求椭圆的离心率;
(II)设M为椭圆上任意一点,点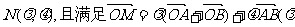 、
、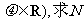 的轨迹方程。
的轨迹方程。
|
(I)已知函数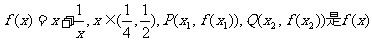 图象上的任意两点,且
图象上的任意两点,且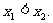
①求直线PQ的斜率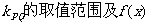 图象上任一点切线的斜率k的取值范围;
图象上任一点切线的斜率k的取值范围;
②由①你得到的结论是:若函数 、
、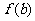 存在,则在
存在,则在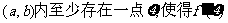 = 成立(用
= 成立(用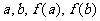 表示,只写出结论,不必证明)
表示,只写出结论,不必证明)
(II)设函数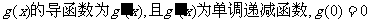 。试运用你在②中得到的结论证明:当
。试运用你在②中得到的结论证明:当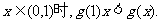
请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题记分。
19.(本小题满分12分)
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2。E、F分别为线段AB、D1C上的点。
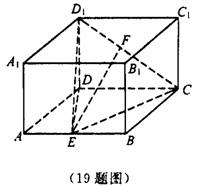 (I)若E、F分别为线段AB、D1C的中点,求证:EF//平面AD1;
(I)若E、F分别为线段AB、D1C的中点,求证:EF//平面AD1;
(II)已知二面角D1-EC-D的大小为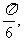 求AE的值。
求AE的值。
18.(本小题满分12分)
设函数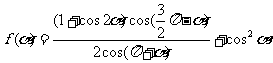
(I)设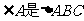 的内角,且为钝角,求
的内角,且为钝角,求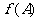 的最小值;
的最小值;
(II)设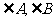 是锐角
是锐角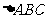 的内角,且
的内角,且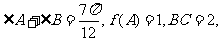 求
求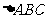 的三个内角的大小和AC边的长。
的三个内角的大小和AC边的长。
17.(本小题满分12分)
电视台举办猜奖活动,参与者需先后回答两道选择题:问题A有四个选项,问题B有六个选项,但都只有一个选项是正确的。正确回答问题A可获奖金m元,正确回答问题B可获奖金n元。
活动规定:①参与者可任意选择回答问题的顺序;②如果第一个问题回答错误,则该参与者猜奖活动中止。
一个参与者在回答问题前,对这两个问题都很陌生,因而准备靠随机猜测回答问题。试确定回答问题的顺序使获奖金额的期望值较大。
16.下列正确结论的序号是 。
①命题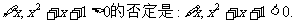
②命题“若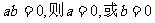 ”的否命题是“
”的否命题是“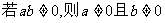 ”
”
③已知线性回归方程是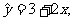 则当自变量的值为2时,因变量的精确值为7。
则当自变量的值为2时,因变量的精确值为7。
④在对两个分类变量进行独立性检验时计算得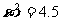 ,就有99%的把握认为这两个分类变量有关系。
,就有99%的把握认为这两个分类变量有关系。
15.已知正四面体ABCD的所有棱长均为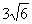 ,顶点A、B、C在半球的底面内,
,顶点A、B、C在半球的底面内,
顶点D在半球面上,且D点在半球底面上的射影为半球的球心,
则此半球的体积
|
14.在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字
之和为奇数的共有 个。
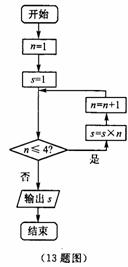
13.右面框图给出的算法执行后输出的结果是 。
12.已知映射: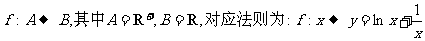 ,对于实数
,对于实数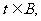 在集合A中不存在原象,则t的取值范围是 ( )
在集合A中不存在原象,则t的取值范围是 ( )
A.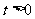 B.
B.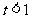 C.
C.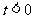 D.
D.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
 第Ⅱ卷 非选择题,共90分
第Ⅱ卷 非选择题,共90分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com