
1. 最近考古学家在陕西、河南等处发现了“长角铜公牛”,该物品约五英尺长,四英尺高,形态极象在拉犁耕地。据右图判断,这幅“长角铜公牛”最早可能是哪个时期的物品?
最近考古学家在陕西、河南等处发现了“长角铜公牛”,该物品约五英尺长,四英尺高,形态极象在拉犁耕地。据右图判断,这幅“长角铜公牛”最早可能是哪个时期的物品?
A.夏朝 B.商朝
C.西周 D.春秋
24.解:由已知得,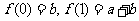
则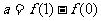 ---------------------------------------------------------------3分
---------------------------------------------------------------3分
则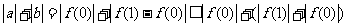 ----------8分
----------8分
则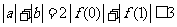 ----------------------------------------------10分
----------------------------------------------10分
|

|
版权所有:()
版权所有:()
23.(1)解: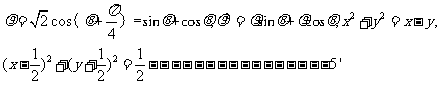
(2)解:直线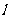 的方程是
的方程是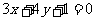 ,圆心到直线
,圆心到直线 的距离为
的距离为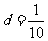 ,
,
则弦长为
22.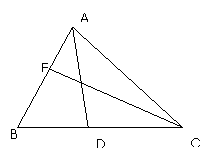 如图,设☉H为
如图,设☉H为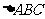 的内切圆,
的内切圆,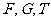 分别为边
分别为边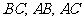 切点,
切点,
则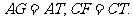 。由
。由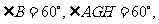 四边形
四边形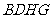 共圆。
共圆。
又 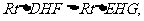 则
则 。
。

21、(本小题满分12分)
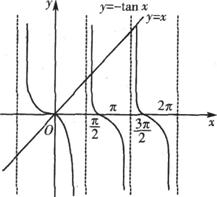

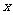 |
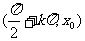 |
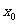 |
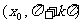 |
|
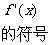 |
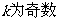 |
- |
0 |
+ |
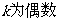 |
+ |
0 |
- |

20.(1)解:设动圆半径为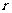 ,则
,则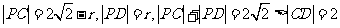 ,由椭圆定义可知,点P的轨迹E是椭圆,其方程为
,由椭圆定义可知,点P的轨迹E是椭圆,其方程为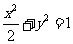 。----------------------------------------------------------------------2分
。----------------------------------------------------------------------2分
① 由已知条件可知,垂足 在以CD为直径的圆周上,则有
在以CD为直径的圆周上,则有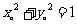 ,又因Q,S,R,T为不同的四个点则可得
,又因Q,S,R,T为不同的四个点则可得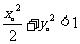 。------------------------------------------------------------------------------4分
。------------------------------------------------------------------------------4分
② 若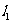 或
或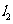 的斜率不存在,易知四边形QRST的面积为2。-----------------------------6分
的斜率不存在,易知四边形QRST的面积为2。-----------------------------6分
若两条直线的斜率存在,设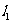 的斜率为
的斜率为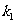 ,则
,则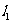 的方程为
的方程为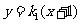
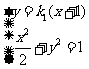 得
得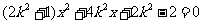 则
则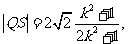 ------8分
------8分
同理可得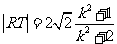
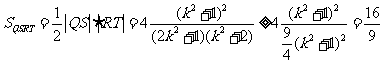
当且仅当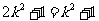 ,即
,即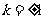 时等号成立。--------------------------------11分
时等号成立。--------------------------------11分
综上所述,当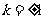 时,四边形QRST的面积取得最小值为
时,四边形QRST的面积取得最小值为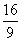 ---------------------------------12分
---------------------------------12分
19.(1)解:记该生到甲,乙,丙,丁四个单位应聘分别为事件B,C,D,E,则P(B)=0.4,P(C)=0.5,P(D)=0.5,P(E)=0.6 。去应聘过的单位数分别是0,1,2,3,4,故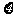 的可能取值是0,2,4--------------2分
的可能取值是0,2,4--------------2分
P(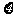 =0)=0.38 P(
=0)=0.38 P(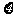 =2)=0.5
P(
=2)=0.5
P(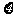 =4)=0.12------------------------
--------------5分
=4)=0.12------------------------
--------------5分
所以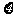 的分布列为
的分布列为
 |
0 |
2 |
4 |
|
P |
0.38 |
0.5 |
0.12 |
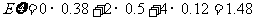 -------------------------------------------------------------------8分
-------------------------------------------------------------------8分
(2)解:因为数列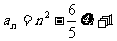 (
(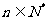 )是严格单调的数列,所以数列
)是严格单调的数列,所以数列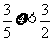 ,
,
即 <
<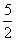 ---------------------------------------------------------------------------------------------------------------10
分
---------------------------------------------------------------------------------------------------------------10
分
P(A)=P( <
<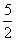 )=P(
)=P( =0)+P(
=0)+P( =2)=0.88------------------------------------------------------------------------------12分
=2)=0.88------------------------------------------------------------------------------12分
18.(本小题满分12分)
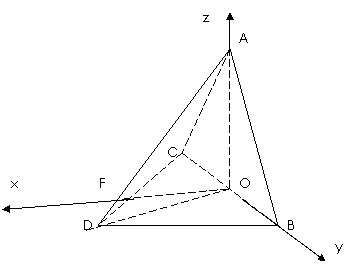
(1)证明:取BC中点O,连接DO,由已知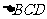 为直角三角形,可得OC=OD=OB,
为直角三角形,可得OC=OD=OB,
又知AB=AC=AD,则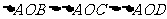 ,-------2分
,-------2分
 可知
可知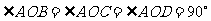 ,则
,则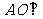 面BCD,
面BCD,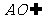 面ABC
面ABC
得面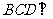 面
面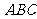 -----------------------------------4分
-----------------------------------4分
(2)解:过O作OF与BC垂直,交CD于F点,
建系[O;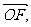 ,
, ,
,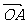 ]则 A(0,0,4), B(0,4,0),
]则 A(0,0,4), B(0,4,0),
C (0,-4,0), D(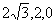 )---------------6分
)---------------6分
设面ACD的法向量为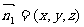 ,由
,由
 ,
,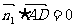 ,可知
,可知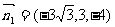 ------8分
------8分
设面ABD的法向量为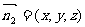 ,由
,由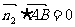 ,
,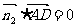 ,可知
,可知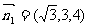 -----------10分
-----------10分
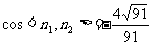 ,则
,则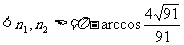 --------------------------------12分
--------------------------------12分
17.(本小题满分12分)
(1)解: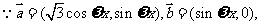
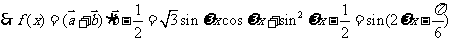 ----------4分
----------4分
由题意可知其周期为 ,故
,故 ,则
,则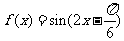 ,
,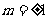 。--------------6分
。--------------6分
(2)解:将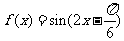 的图像向左平移
的图像向左平移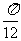 ,得到
,得到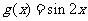 ,-------------------8分
,-------------------8分
由其对称性,可设交点横坐标分别为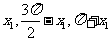 , 有
, 有
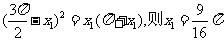 ------------------------------------------------------------10分
------------------------------------------------------------10分
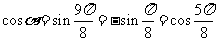 则
则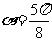 ------------------------------------------------------12分
------------------------------------------------------12分
13. 14.
14. 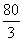 15.4 16.①③④
15.4 16.①③④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com