
第一节:单项填空(共15小题,每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
21.More than five doctors and rescuers have got to Yushu County up to now.
A.thousand B.thousands C.thousand of D.thousands of
20.(本小题满分14分)
已知函数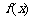 的图象在
的图象在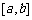 上连续不断,定义:
上连续不断,定义:
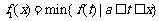
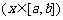 ,
,
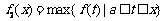
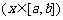 .
.
其中,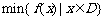 表示函数
表示函数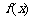 在
在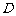 上的最小值,
上的最小值,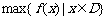 表示函数
表示函数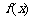 在
在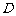 上的最大值.若存在最小正整数
上的最大值.若存在最小正整数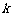 ,使得
,使得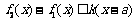 对任意的
对任意的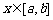 成立,则称函数
成立,则称函数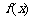 为
为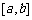 上的“
上的“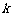 阶收缩函数”.
阶收缩函数”.
(Ⅰ)若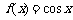 ,
,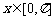 ,试写出
,试写出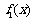 ,
,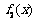 的表达式;
的表达式;
(Ⅱ)已知函数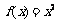 ,
,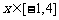 ,试判断
,试判断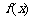 是否为
是否为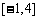 上的“
上的“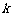 阶收缩函数”,如果是,求出对应的
阶收缩函数”,如果是,求出对应的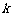 ;如果不是,请说明理由;
;如果不是,请说明理由;
(Ⅲ)已知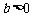 ,函数
,函数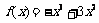 是
是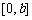 上的2阶收缩函数,求
上的2阶收缩函数,求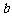 的取值范围.
的取值范围.
海淀区高三年级第二学期期末练习
数 学 (理)
19.(本小题满分13分)
已知椭圆 和抛物线
和抛物线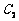 有公共焦点F(1,0),
有公共焦点F(1,0),  的中心和
的中心和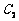 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线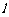 与抛物线
与抛物线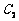 分别相交于A,B两点.
分别相交于A,B两点.
(Ⅰ)写出抛物线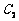 的标准方程;
的标准方程;
(Ⅱ)若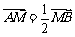 ,求直线
,求直线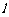 的方程;
的方程;
(Ⅲ)若坐标原点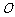 关于直线
关于直线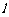 的对称点
的对称点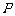 在抛物线
在抛物线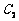 上,直线
上,直线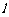 与椭圆
与椭圆 有公共点,求椭圆
有公共点,求椭圆 的长轴长的最小值.
的长轴长的最小值.
18.(本小题满分13分)
已知函数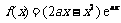 ,其中a为常数,且
,其中a为常数,且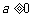 .
.
(Ⅰ)若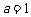 ,求函数
,求函数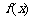 的极值点;
的极值点;
(Ⅱ)若函数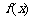 在区间
在区间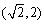 上单调递减,求实数a的取值范围.
上单调递减,求实数a的取值范围.
17.(本小题满分13分)
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(Ⅰ)求4人恰好选择了同一家公园的概率;
(Ⅱ)设选择甲公园的志愿者的人数为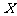 ,试求
,试求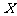 的分布列及期望.
的分布列及期望.
16.(本小题满分14分)
 已知四棱锥
已知四棱锥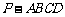 ,底面
,底面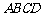 为矩形,侧棱
为矩形,侧棱 ,其中
,其中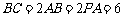 ,
,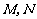 为侧棱
为侧棱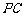 上的两个三等分点,如图所示.
上的两个三等分点,如图所示.
(Ⅰ)求证: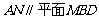 ;
;
(Ⅱ)求异面直线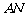 与
与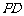 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求二面角 的余弦值.
的余弦值.
15.(本小题满分13分)
记等差数列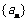 的前n项和为
的前n项和为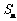 ,已知
,已知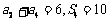 .
.
(Ⅰ)求数列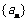 的通项公式;
的通项公式;
(Ⅱ)令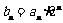
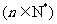 ,求数列
,求数列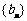 的前n项和
的前n项和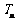 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com