
7.某溶液中存在五种离子:NO3-、SO42-、Fe3+、H+和R离子,其物质的量之比为2:3:1:3:1,则R可能为( )
A.Fe2+ B.M g2+
C.C1-  Ba2+
Ba2+
6.2009年3月20日,国家质检总局发布消息称,目前市场上销售的强生、妙思乐及帮宝适等婴儿卫浴产品常常标有“温和”、“纯净”等字样,但其中却含有甲醛以及1,4-二氧杂环乙烷等有害物质。1,4-二氧杂环乙烷的结构简式为 ,下列有关其性质的叙述k_s_5_u正确的是 ( )
,下列有关其性质的叙述k_s_5_u正确的是 ( )
A.1,4-二氧杂环乙烷与丁酸互为同分异构体
B.1,4-二氧杂环乙烷与乙酸乙酯互为同系物
C.1,4-二氧杂环乙烷与钠反应可放出氢气
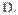 1,4-二氧杂环乙烷的分子间可形成氢键
1,4-二氧杂环乙烷的分子间可形成氢键
5.图甲和图乙表示某种生物种群中个体数量和年龄的关系曲线,如不考虑其他因素,种群甲和种群乙的年龄组成分别属于( )

A.衰退型和增长型 B.增长型和衰退型
C.稳定型和衰退型  稳定型和增长型
稳定型和增长型
4.下列甲、乙、丙三图分别表示有关生物学过程,对其曲线变化描述中,k_s_5_u正确的是( )
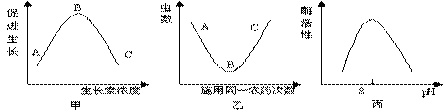
①甲图A点时的生长素浓度促进植物生长,C点时的生长素浓度抑制生长;②甲图B点时的浓度若为茎背光一侧的生长素浓度,C点时的浓度不可能为茎向光一侧的生长素浓度;③乙图B点时,害虫种群抗药个体占百分比大于A点害虫种群抗药个体所占百分比;④乙图A点时,害虫不存在抗药个体;⑤丙图曲线表示胰麦芽糖酶对淀粉水解为麦芽糖的催化特性;⑥丙图曲线表示肠脂肪酶对脂肪水解为甘油和脂肪酸的催化特性;
A. ①④⑤ B. ①④⑥ C. ②③⑤
 ②③⑥
②③⑥
3.生物学研究成果已广泛应用到生产、医药等领域。下列叙述中符合这种情况的是( )
①应用以虫治虫、以菌治菌的措施,可以减少或避免有机农药污染;②根据DNA分子的特异性,进行亲子鉴定;③基于细胞呼吸的原理,采用套种、合理密植、大棚种植等措施增加作物产量;④在细胞膜的功能研究基础上,开发人工“肾”治疗尿毒症;⑤对于花卉的优良变异品种,可用嫁接的方法保存或用植物组织培养进行扩种;
A.①②③④ B.①②④⑤ C.①③④⑤  ②③④⑤
②③④⑤
2.a、b、c、d分别是一些生物细胞某个分裂时期示意图,下列有关描述k_s_5_u正确的是( )

A.a图表示植物细胞有丝分裂后期
B.b图表示人红细胞分裂的某个阶段
C.c图细胞分裂后将产生1个卵细胞和1个极体
 d图细胞中含有4条染色单体
d图细胞中含有4条染色单体
1.向一定浓度的淀粉溶液中加入适量的唾液淀粉酶,37℃水浴保温后再加入适量的双缩脲试剂,摇匀观察试管中溶液的变化k_s_5_u现象应该是( )
A.产生砖红色沉淀 B.溶液呈蓝色 C.溶液呈紫色  溶液不变化
溶液不变化
22.本小题满分12分)已知等比数列{an}中,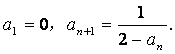
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,证明: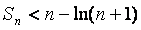 ;
;
(Ⅲ)设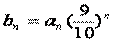 ,证明:对任意的正整数n、m,均有
,证明:对任意的正整数n、m,均有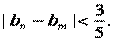
21.(本小题满分12分)已知椭圆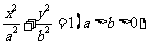 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线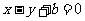 是抛物线
是抛物线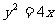 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点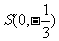 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ?
若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ?
若存在,求点T坐标;若不存在,说明理由.
20.(本小题满分12分)已知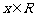 ,函数
,函数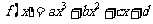 在
在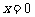 处取得极值,曲线
处取得极值,曲线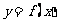 过原点
过原点 和点
和点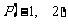 .若曲线
.若曲线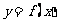 在点
在点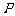 处的切线
处的切线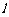 与直线
与直线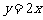 的夹角为
的夹角为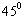 ,且直线
,且直线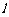 的倾斜角
的倾斜角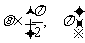
(Ⅰ)求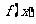 的解析式;
的解析式;
(Ⅱ)若函数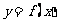 在区间
在区间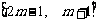 上是增函数,求实数
上是增函数,求实数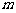 的取值范围;
的取值范围;
(Ⅲ)若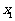 、
、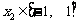 ,求证:
,求证: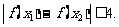
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com