
5、函数f(x)=|sinx|的一个单调递增区间是( )
A.[-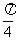 ,
,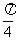 ] B.[
] B.[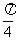 ,
,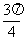 ] C.[
] C.[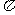 ,
,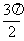 ] D.[
] D.[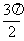 ,2
,2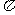 ]
]
4、过空间一定点P的直线中,与长方体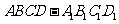 的12条棱所在直线成等角的直线共有( )
的12条棱所在直线成等角的直线共有( )
A.0条 B.1条 C.4条 D.无数条
3、某汽车经销商在国庆长假中销售了高级轿车54辆,中级轿车108辆,经济型轿车162辆,现要对其中36辆车进行售后调查,为了使调查更具代表性,则应选( )
A. 高级轿车4辆,中级轿车14辆,经济型轿车18辆
B. 高级轿车6辆,中级轿车12辆,经济型轿车18辆
C. 高级轿车8辆,中级轿车12辆,经济型轿车16辆
D. 高级轿车10辆,中级轿车12辆,经济型轿车14辆
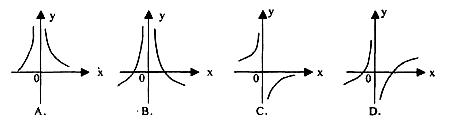
2、函数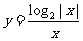 的大致图象是 ( )
的大致图象是 ( )
1、已知集合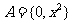 ,
,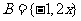 ,若
,若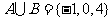 ,则
,则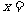 ( )
( )
A.4 B.2 C.  D.0或2
D.0或2
6. 已知函数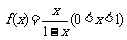 的反函数为
的反函数为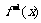 ,数列
,数列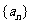 和
和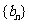 满足:
满足: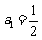 ,
,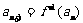 ,函数
,函数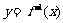 的图象在点
的图象在点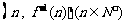 处的切线在
处的切线在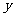 轴上的截距为
轴上的截距为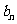 .
.
(Ⅰ)求数列{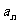 }的通项公式;
}的通项公式;
(Ⅱ)若数列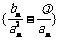 的项仅
的项仅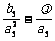 最小,求
最小,求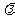 的取值范围;
的取值范围;
(Ⅲ)令函数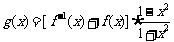 ,
,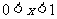 ,数列
,数列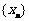 满足:
满足: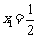 ,
,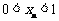 ,且
,且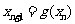 ,其中
,其中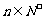 .证明:
.证明: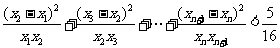 .
.
5.已知 ,点
,点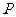 满足
满足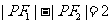 ,记点
,记点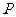 的轨迹为
的轨迹为 .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)若直线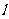 过点
过点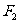 且与轨迹
且与轨迹 交于
交于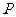 、
、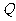 两点. (i)设点
两点. (i)设点
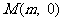 ,问:是否存在实数
,问:是否存在实数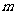 ,使
,使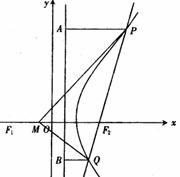 得直线
得直线 绕点
绕点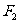 无论怎样转动, 都有
无论怎样转动, 都有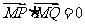 成立?若存在,求出实数
成立?若存在,求出实数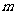 的值;若不存在,请说明理由.(ii)过
的值;若不存在,请说明理由.(ii)过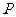 、
、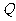 作直线
作直线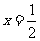 的垂线
的垂线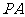 、
、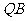 ,垂足分别为
,垂足分别为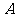 、
、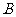 ,记
,记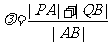 ,求
,求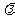 的取值范围.
的取值范围.
4.已知函数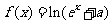 (
(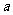 为常数)是R上的奇函数,函数g(x)=
为常数)是R上的奇函数,函数g(x)=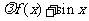 是区间
是区间 上的减函数.
上的减函数.
(Ⅰ)求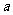 的值;
的值;
(Ⅱ)若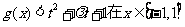 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程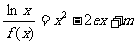 的根的个数.
的根的个数.
3.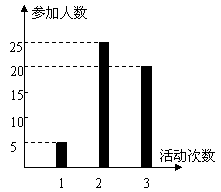 按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活
按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活
动(以下简称活动). 该校高2010级一班50名学生在上学期参加活动
的次数统计如图所示.
(I)从该班任意选两名学生,求他们参加活动次数不相等的概率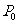 .
.
(II)从该班中任选两名学生,用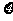 表示这两人参加活动次数之差的
表示这两人参加活动次数之差的
绝对值,求随机变量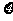 的分布列及数学期望
的分布列及数学期望 .
.
(III)从该班中任选两名学生,用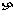 表示这两人参加活动次数之和,
表示这两人参加活动次数之和,
记 “函数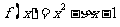 在区间
在区间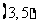 上有且只有一个零点”为事件A,求事件A发生的概率.
上有且只有一个零点”为事件A,求事件A发生的概率.
2.如图,四棱锥P-ABCD的底面是边长为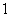 的正方形,
的正方形,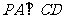 ,
,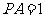 ,
,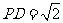 ,
, 为
为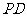 上一点,
上一点,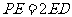 .
.
(Ⅰ)求证: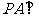 平面
平面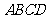 ;
;
(Ⅱ)求二面角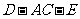 的正切值;
的正切值;
(Ⅲ)在侧棱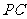 上是否存在一点
上是否存在一点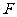 ,使得
,使得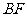 ∥平面
∥平面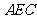 ,若存在,指出
,若存在,指出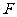 点位置,并证明,若不存在,说明理由.
点位置,并证明,若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com