
42. (12分) 我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径
我国计划发射火星探测器,该探测器的运行轨道是以火星(其半径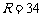 百公里)的中心
百公里)的中心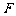 为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点)
为一个焦点的椭圆. 如图,已知探测器的近火星点(轨道上离火星表面最近的点) 到火星表面的距离为
到火星表面的距离为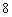 百公里,远火星点(轨道上离火星表面最远的点)
百公里,远火星点(轨道上离火星表面最远的点)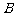 到火星表面的距离为800百公里. 假定探测器由近火星点
到火星表面的距离为800百公里. 假定探测器由近火星点 第一次逆时针运行到与轨道中心
第一次逆时针运行到与轨道中心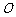 的距离为
的距离为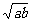 百公里时进行变轨,其中
百公里时进行变轨,其中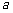 、
、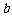 分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
分别为椭圆的长半轴、短半轴的长,求此时探测器与火星表面的距离(精确到1百公里).
解:设所求轨道方程为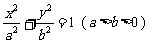 ,
,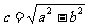 .
.
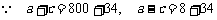 ,
,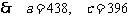 .
.
于是 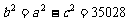 .
.
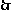 所求轨道方程为
所求轨道方程为 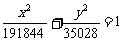 .
.
设变轨时,探测器位于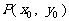 ,则
,则
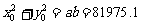 ,
,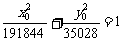 ,
,
解得 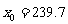 ,
,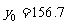 (由题意).
(由题意).
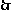 探测器在变轨时与火星表面的距离为
探测器在变轨时与火星表面的距离为
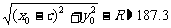 .
.
答:探测器在变轨时与火星表面的距离约为187百公里.
41. (12分)已知点(x, y)是曲线C上任意一点,将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程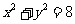 ;定点M(2,1),平行于OM的直线
;定点M(2,1),平行于OM的直线 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线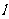 与曲线C交于A、B两个不同点.
与曲线C交于A、B两个不同点.
(1)求曲线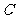 的方程;
的方程;
(2)求m的取值范围.
解:
(1)在曲线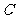 上任取一个动点P(x,y),
上任取一个动点P(x,y),
则点(x,2y)在圆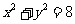 上.
上.
所以有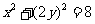 . 整理得曲线C的方程为
. 整理得曲线C的方程为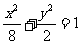 . …
. …
(2)∵直线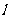 平行于OM,且在y轴上的截距为m,又
平行于OM,且在y轴上的截距为m,又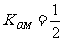 ,
,
∴直线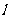 的方程为
的方程为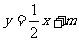 .
.
由 , 得
, 得 
∵直线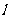 与椭圆交于A、B两个不同点,
与椭圆交于A、B两个不同点,
∴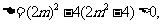
解得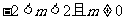 .
.
∴m的取值范围是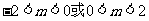 .
.
40.
(12分)已知函数 ,
,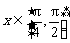 .
.
(1)求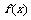 的最大值和最小值;
的最大值和最小值;
(2)若不等式 在
在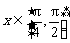 上恒成立,求实数
上恒成立,求实数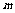 的取值范围.
的取值范围.
解:(1)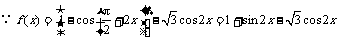
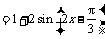 .
.
又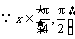 ,
,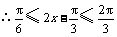 ,即
,即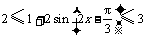 ,
,
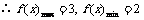 .
.
(2)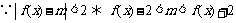 ,
,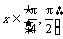 ,
,
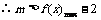 且
且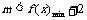 ,
,
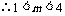 ,即
,即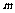 的取值范围是
的取值范围是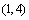 .
.
39. (8分)由直线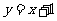 上的点A向圆
上的点A向圆 引切线,切点为P,求
引切线,切点为P,求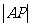 的最小值.
的最小值.
解:设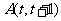 为直线上任意一点,
为直线上任意一点,
由题知: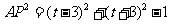
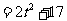 ,
,
所以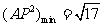 ,得解.
,得解.
38. (8分)已知A(3,2),B(-2,7),若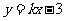 与线段AB相交,求
与线段AB相交,求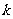 的取值范围.
的取值范围.
解:直线方程可化为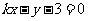 ,
,
则 ,
,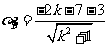 ,
,
由题知,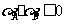 即
即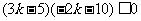
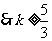 或
或 .
.
37. 若方程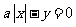 和
和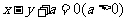 所确定的曲线有两个交点,则
所确定的曲线有两个交点,则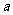 的取值范围为
( B )
的取值范围为
( B )
A. 或
或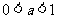 B.
B. C.
C.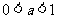 D.
D.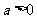
36. 方程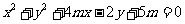 表示圆的充要条件是
( B )
表示圆的充要条件是
( B )
A.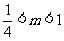 B.
B.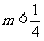 或
或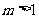 C.
C.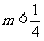 D.
D.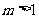
35. 若点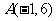 、
、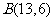 到直线
到直线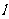 的距离都等于6,则满足条件的直线
的距离都等于6,则满足条件的直线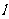 有 ( D )
有 ( D )
A.1条 B.2条 C.3条 D.4条
34. 空间四点中,其中三点共线是四点共面的 ( A )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
33. 已知AB是椭圆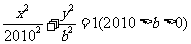 的长轴,若把该长轴2010等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点
的长轴,若把该长轴2010等分,过每个等分点作AB的垂线,依次交椭圆的上半部分于点 ,设左焦点为
,设左焦点为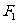 ,则
,则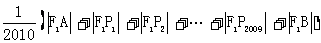 = 2011 .
= 2011 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com