
1.数列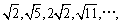 则
则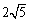 是该数列的( )
是该数列的( )
A.第6项 B.第7项 C.第10项 D.第11项
14. 已知数列{ an}的通项公式an与前n项和公式Sn之间满足关系Sn=2-3an
(1)求a1;
(2)求an与an (n≥2,n∈N*)的递推关系;
(3)求Sn与Sn (n≥2,n∈N*)的递推关系,
 必修5
第2章
数列
必修5
第2章
数列
§2.2等差数列、等比数列
重难点:理解等差数列、等比数列的概念,掌握等差数列、等比数列的通项公式与前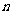 项和公式,能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
项和公式,能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
考纲要求:①理解等差数列、等比数列的概念.
②掌握等差数列、等比数列的通项公式与前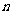 项和公式.
项和公式.
③能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
④了解等差数列与一次函数、等比数列与指数函数的关系.
经典例题:已知一个数列{an}的各项是1或3.首项为1,且在第k个1和第k+1个1之间有2k-1个3,即1,3,1,3,3,3,1,3,3,3,3,3,1,…,记该数列的前n项的和为Sn.
(1)试问第2006个1为该数列的第几项?
(2)求a2006;
(3)求该数列的前2006项的和S2006;
当堂练习:
13. 已知数列{ an}满足a1=0,an+1+Sn=n2+2n(n∈N*),其中Sn为{ an}的前n项和,求此数列的通项公式.
12. 已知数列{ an}中a1=1,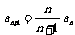 (1)写出数列的前5项;(2)猜想数列的通项公式.
(1)写出数列的前5项;(2)猜想数列的通项公式.
11. 下面分别是数列{ an}的前n项和an的公式,求数列{ an}的通项公式:
(1)Sn=2n2-3n; (2)Sn=3n-2
10.设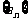 是首项为1的正项数列,且
是首项为1的正项数列,且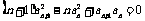 (
( =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是 =________.
=________.
9.已知数列{ an}的前n项和公式Sn=n2+2n+5,则a6+a7+a8= .
8.已知数列{ an}满足a1=1 , an+1=c an+b, 且a2 =3,a4=15,则常数c,b 的值为 .
7.在数列{ an}中,已知an=2,an= an+2n,则a4 +a6 +a8的值为 .
6.若数列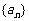 前8项的值各异,且
前8项的值各异,且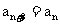 对任意的
对任意的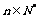 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍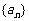 前8项值的数列为
( )
前8项值的数列为
( )
A.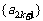 B.
B.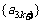 C.
C.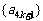 D.
D.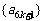
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com