5.下列各句中，没有语病的一项是

A.考生普遍感觉，国家公务员现在越来越难考了，要想拿高分，就要成为博学专家，武器、科技、能源、经济、政治、军事、管理等方面均要有涉猎。

B.与科幻电影中的遐想不同，汽车工业在电气化、物联网、车联网、3G等新名词的簇拥下，已经踏步在技术变革的十字路口，呈现蓄势待发的态势。

C.汉王电纸书与欧美地区产品同步推出，并透露了带有手写识别能力的升级版发布计划，在德国汉诺威展会上成为热门产品。

　 D.根据群众举报，市检察院领导商请市审计局指派人员到金阳分校查账，几天来，审计局的同志在查阅这个分校基建部分账目。

4.下列各句中，加点的熟语使用正确的一项是

A.学习钢琴要勤奋，且贵在坚持，每天练几个小时，长此以往，必将获得不菲的成就。

B.现在还有些司机不吸取血的教训，仍然酒后驾车，对这种火中取栗的行为，公安交通部门还应加大处罚力度。

C.观众们对电影《三枪拍案惊奇》提出强烈批评，并不是对张艺谋吹毛求疵，而是恨铁不成钢的表现。

D.大学生开始职业生涯规划时要瞻前顾后，要从个人兴趣、个人特质及专业特点出发，并不是证书多了就业之路就宽了。

3.依次填入下列各句横线处的词语，最恰当的一组是

①少数用工企业受利益驱动，　　 《劳动合同法》条文，对职工搞起了“劝退”活动，在社会上造成了恶劣影响。

②有些运动员在大赛前心理负担过重，因而比赛时表现失常。这种情况已经成了一种难以

　　 的怪现象。

③风闻央视主持人王小丫的一幅水墨画，竟然卖出了4800万的天价，不少人先是吃惊，

　　　 感到非常有趣：王小丫的一幅画真的值4800万吗？

A.曲解　 捉摸　 继而　　　　 B.误解　 捉摸　 既而

C.曲解　 琢磨　 既而　　　　 D.误解　 琢磨　 继而

2.下列词语中，没有错别字的一组是

A．一厢情愿　　 录像器材　　 流光溢彩　　 喝采之声

B．呜呼哀哉　　 哀声叹气　　 波澜壮阔　　 意兴阑珊

C．鸠占鹊巢　　 门可罗雀　　 高档家俱　　 与时俱进

D．贸然行事　　 贸易往来　　 众口铄金　　 闪烁其辞

1.下列词语中加点的字，读音全都不相同的一组是

A.证券　　 蜷伏　　 甲醛　　 怙恶不悛

B.酗酒　　 畏葸　　 旭日　　 嘘寒问暖

C.纰漏　　 毗邻　　 譬如　　 匹夫之勇

D.不啻　　 鞭笞　　 踟躇　　 持之以恒

3、函数y=e^-x 的图像与函数_____________的图像关于原点对称。

4　 关于x的方程|x-1|=kx+2有两个不同的实根，则k的范围为_____________

[学后反思]____________________________________________________ _______

　　　　　 _____________________________________________________________

　　　　　 ____________________________________________________________

2、若函数y=f(2x+1)的图像有唯一的对称轴，其方程为x=0,则函数y=f(2x-1)的图像的对称轴方程为_____________

1、已知函数f(x)是R上的奇函数，则函数y=f(x-3)+2的图像经过的定点为_____________

4．若对于定义域内的任意x，若f (a－x)＝f (a+x) (或f (x)＝f (2a－x))，则f (x)关于　　　 对称，若f (a－x)+f (a+x)＝2b (或f (x)+f (2a－x)＝2b)，则f (x)关于　　　 对称.

　[典型例析]

例1　 作出下列函数的图象.

(1)y=|x-x²|　　　　 (2)y=x-|x²|　　　　　 (3)y=;　.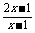

变式训练1：作出下列各个函数的图象：(1)y=2-2^x； (2)y=|log(1-x)|；

(3)y=.

小结：

例2　 设函数f(x)=x²-2|x|-1 (-3≤x≤3).

(1)证明：f(x)是偶函数；

(2)画出函数的图象；

(3)指出函数f(x)的单调区间，并说明在各个单调区间上f(x)是增函数还是减函数；

(4)求函数的值域.

变式训练2:已知函数f(x)=x|m-x| (x∈R)，且f(4)=0

(1)求实数m的值

(2)做出函数f(x)的图像

　　　 (3)根据图像指出f(x)的单调减区间

　　　 (4) 根据图像写出不等式f(x)>0的解集

小结：

[当堂检测]

3．伸缩变换：

① y＝Af (x) (A>0)的图象是将y＝f(x)的图象的　　 .

② y＝f (ax) (a>0)的图象是将y＝f(x)的图象的　　　 .