
所以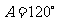 …………………………………………………………5分
…………………………………………………………5分
(Ⅱ)由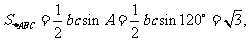 得
得
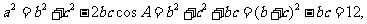 所以
所以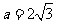 ………12分
………12分
18、解:(Ⅰ)当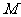 为棱
为棱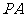 中点时,
中点时,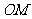 ∥平面
∥平面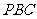 .
.
证明如下:
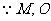 分别为
分别为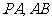 中点,
中点,
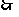
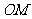 ∥
∥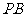
又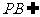 平面
平面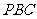 ,
,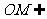 平面
平面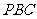
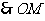 ∥平面
∥平面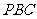 . …………………………………………………………3分
. …………………………………………………………3分
(Ⅱ)连结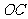 ,
,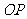
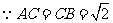 ,
,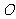 为
为 中点,
中点,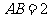 ,
,
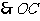 ⊥
⊥ ,
,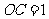 .
.
同理, 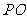 ⊥
⊥ ,
,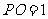 .又
.又 ,
,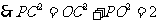 ,
,
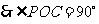 .
. 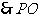 ⊥
⊥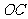 .
.

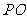 ⊥
⊥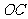 ,
,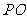 ⊥
⊥ ,
,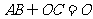 ,
,
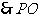 ⊥平面
⊥平面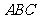 .
. 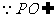 平面
平面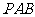
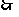 平面
平面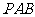 ⊥平面
⊥平面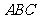 ....7分
....7分
(Ⅲ)如图,建立空间直角坐标系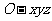 .
.

则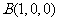 ,
,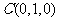 ,
,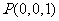 ,
,
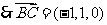 ,
,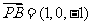 .
.
由(Ⅱ)知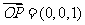 是平面
是平面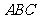
的一个法向量.
设平面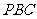 的法向量为
的法向量为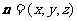 ,
,
则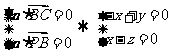 .
.
令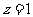 ,则
,则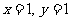 ,
,
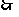 平面
平面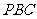 的一个法向量
的一个法向量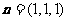 .
.
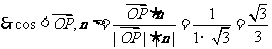 .
.
 二面角
二面角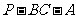 的平面角为锐角,
的平面角为锐角,
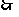 所求二面角
所求二面角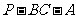 的余弦值为
的余弦值为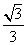 . ………………………12分
. ………………………12分
13、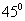 14、3
15、
14、3
15、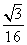 16、③④
16、③④
1---------6 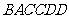 7---------12
7---------12 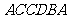
22.(本小题满分14分)已知数列 中,
中,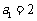 ,对于任意的
,对于任意的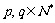 ,有
,有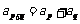
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列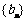 满足:
满足: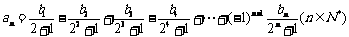 ,
,
求数列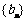 的通项公式;
的通项公式;
(Ⅲ)设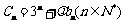 ,是否存在实数
,是否存在实数 ,当
,当 时,
时,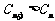 恒成立,若存在,求实数
恒成立,若存在,求实数 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
高2010级热身考试文科数学参答
21. (本小题满分12分)已知椭圆的中心在原点,焦点在 轴上,经过点
轴上,经过点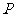
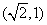 且离心率
且离心率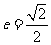 .过定点
.过定点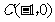 的直线与椭圆相交于
的直线与椭圆相交于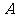 ,
,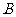 两点.
两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)在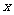 轴上是否存在点
轴上是否存在点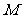 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点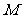 的坐标;若不存
的坐标;若不存
在,请说明理由.
20. (本小题满分12分)已知函数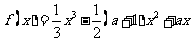 .
.
(Ⅰ)求 的单调递增区间;
的单调递增区间;
(Ⅱ)若 在
在 处取得极值,且方程:
处取得极值,且方程: 有三个不等实根,求实数
有三个不等实根,求实数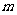 的取值范围。
的取值范围。

19. (本小题满分12分) 2010年世博会于5月1日在中国上海隆重开幕,甲、乙、丙三人打算利用周六去游览,由于时间有限,三人商定在已圈定的10个国家馆中各自随机选择一个国家馆游览(选择每个国家馆的可能性相同) .
(Ⅰ)求甲、乙、丙三人同时游览同一个国家馆的概率;
(Ⅱ)求甲、乙、丙三人中至少有两人同时游览同一个国家馆的概率。
18. (本小题满分12分) 在三棱锥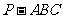 中,
中,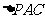 和
和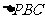 是边长为
是边长为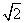 的等边三角形,
的等边三角形,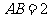 ,
,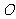 是
是 中点.
中点.
(Ⅰ)在棱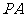 上求一点
上求一点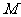 ,使得
,使得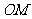 ∥平面
∥平面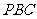 ;
;
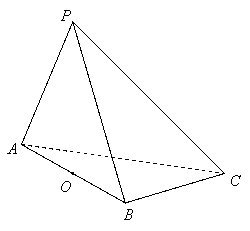 (Ⅱ)求证:平面
(Ⅱ)求证:平面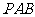 ⊥平面
⊥平面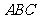 ;
;
(Ⅲ)求二面角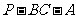 的余弦值.
的余弦值.
17.(本小题满分12分)已知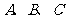 为
为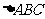 的三内角,且其对边分别为
的三内角,且其对边分别为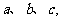 若
若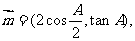
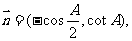 且
且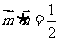 .
.
(Ⅰ)求角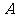 ;
;
(Ⅱ)若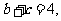
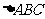 的面积为
的面积为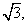 求
求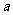 .
.
16.有下列命题:
①函数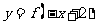 与
与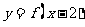 的图象关于
的图象关于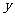 轴对称;
轴对称;
②定义在 上的函数
上的函数 满足
满足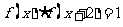 ,则函数
,则函数 的最小正周期为2;
的最小正周期为2;
③若函数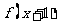 为奇函数,则函数
为奇函数,则函数 的图像关于点
的图像关于点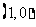 中心对称;
中心对称;
④若函数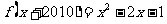 (x∈
(x∈ ),则函数
),则函数 的最小值为
的最小值为 .
.
其中真命题的序号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com