
18.(本小题满分12分)
为保护水资源,宣传节约用水,某校4名志愿者准备去附近的甲、乙、丙三家公园进行宣传活动,每名志愿者都可以从三家公园中随机选择一家,且每人的选择相互独立.
(Ⅰ)求4人恰好选择了同一家公园的概率;
(Ⅱ)设选择甲公园的志愿者的人数为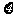 ,试求
,试求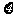 的分布列及期望.
的分布列及期望.
17. (本小题满分12分)已知函数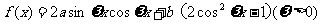 在
在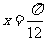 时取最大值2。
时取最大值2。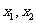 是集合
是集合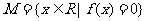 中的任意两个元素,|
中的任意两个元素,| |的最小值为
|的最小值为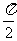 。
。
(I)求a、b的值;
(II)若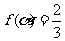 ,求
,求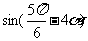 的值。
的值。
16、给出下列命题:
①函数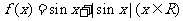 的最小正周期是
的最小正周期是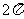 ;
;
②已知函数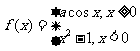 在
在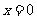 处连续,则
处连续,则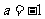 ;
;
③函数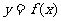 与
与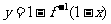 的图象关于直线
的图象关于直线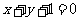 对称;
对称;
④将函数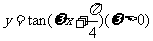 的图象按向量
的图象按向量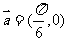 平移后,与函数
平移后,与函数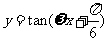 的图象重合,则
的图象重合,则 的最小值为
的最小值为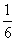 ,你认为正确的命题有:
。
,你认为正确的命题有:
。
15、设曲线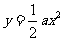 在点
在点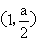 处的切线与直线
处的切线与直线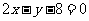 平行,又已知圆
平行,又已知圆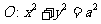 和点
和点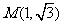 ,则过点M且与圆O相切的直线与两坐标轴围成的三角形的面积等于_____________
,则过点M且与圆O相切的直线与两坐标轴围成的三角形的面积等于_____________
14、我校在上次摸考中约有1000人参加考试,数学考试的成绩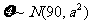 (
(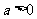 ,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的
,试卷满分150分),统计结果显示数学考试成绩在70分到110分之间的人数约为总人数的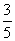 ,则此次数学考试成绩不低于110分的学生约有 人。
,则此次数学考试成绩不低于110分的学生约有 人。
13、设等比数列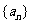 的前
的前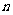 项和为
项和为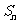 ,且
,且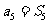 ,则
,则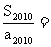 _____________.
_____________.
12、定义在 上的函数
上的函数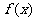 满足数列
满足数列 ,当
,当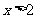 时,
时,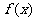 单调递增。如果
单调递增。如果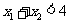 ,且
,且 ,则
,则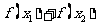 的值 ( )
的值 ( )
A.恒小于0 B.恒大于0 C.可能为0 D.可正可负
第Ⅱ卷
11、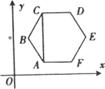 如图正六边形
如图正六边形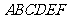 中,
中,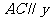 轴.从六个顶点中任取三点,使这三点能确定一条形如
轴.从六个顶点中任取三点,使这三点能确定一条形如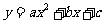 (
( )的抛物线的概率是( )
)的抛物线的概率是( )
A.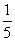 B.
B.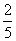 C.
C.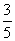 D.
D.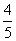
10、已知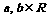 ,若关于
,若关于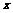 的方程
的方程 的实根
的实根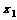 和
和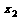 满足-1≤
满足-1≤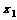 ≤1,1≤
≤1,1≤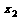 ≤2,则在平面直角坐标系aOb中,点(
≤2,则在平面直角坐标系aOb中,点(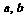 )所表示的区域内的点P到曲线
)所表示的区域内的点P到曲线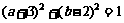 上的点Q的距离|PQ|的最小值为
( )
上的点Q的距离|PQ|的最小值为
( )
A.3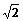 -1 B.2
-1 B.2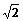 -1 C.3
-1 C.3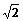 +1 D.2
+1 D.2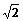 +1
+1
9、若存在过点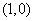 的直线与曲线
的直线与曲线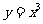 和
和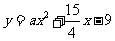 都相切,则
都相切,则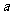 等于( )
等于( )
A.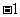 或
或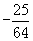 B.
B.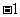 或
或 C.
C. 或
或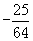 D.
D. 或
或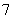
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com