
1.下列词语中加点的字,每对的读音都不相同的一组是
A.刊载/千载难逢 落拓/丢三落四 叱咤/姹紫嫣红
B.苗圃/惊魂甫定 躯壳/金蝉脱壳 饮马/饮水思源
C.供奉/供不应求 露脸/抛头露面 扛枪/力能扛鼎
D.鲜艳/鲜为人知 宁愿/息事宁人 炮制/炮烙之刑
7.已知多项式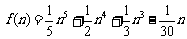 .
.
(Ⅰ)求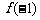 及
及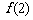 的值;
的值;
(Ⅱ)试探求对一切整数n,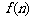 是否一定是整数?并证明你的结论.
是否一定是整数?并证明你的结论.
5.如图所示的几何体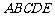 中,
中,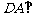 平面
平面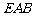 ,
,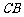 ∥
∥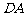 ,
,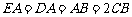 ,
,

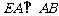 ,
,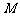 是
是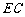 的中点.
的中点.
(1)求证: ;
;
(2)求二面角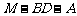 的余弦值.
的余弦值.
6学校文娱队的每位队员唱歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中选2人.设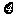 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且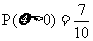 .
.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出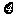 的概率分布列并计算
的概率分布列并计算 .
.
4.过点A(2,1)作曲线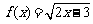 的切线l.
的切线l.
(Ⅰ)求切线l的方程;
(Ⅱ)求切线l,x轴及曲线所围成的封闭图形的面积S.
3.变换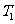 是逆时针旋转
是逆时针旋转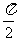 的旋转变换,对应的变换矩阵是
的旋转变换,对应的变换矩阵是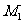 ;变换
;变换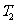 对应用的变换矩阵是
对应用的变换矩阵是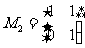 。
。
(Ⅰ)求点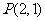 在
在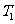 作用下的点
作用下的点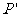 的坐标;
的坐标;
(Ⅱ)求函数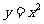 的图象依次在
的图象依次在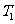 ,
,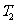 变换的作用下所得曲线的方程。
变换的作用下所得曲线的方程。
2.如图所示的正方形被平均分成16个部分,向大正方形区域随
即地投掷一个点(每次都能投中),设投中最左侧的四个正方形
区域的事件为A,投中最上面4个正方形或右下角的正方形区
 域的事件为B.求
域的事件为B.求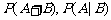 .
.
1.若两条曲线的极坐标方程分别为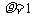 与
与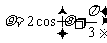 ,它们相交于
,它们相交于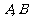 两点,求线段
两点,求线段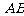 的长.
的长.
22.(本小题满分14分)
设数列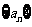 ,
,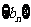 满足:a1=4,a2=
满足:a1=4,a2=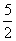 ,
,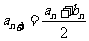 ,
, 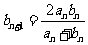 .
.
(1)用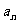 表示
表示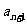 ;并证明:对任意
;并证明:对任意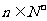 , an>2
;
, an>2
;
(2)证明: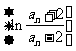 是等比数列;
是等比数列;
(3)设Sn是数列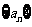 的前n项和,当n≥2时,Sn与
的前n项和,当n≥2时,Sn与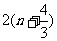 是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
是否有确定的大小关系?若有,加以证明;若没有,请说明理由.
20.(本小题满分12分)
已知函数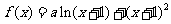 ,其中,
,其中,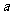 为实常数且
为实常数且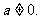
(Ⅰ)求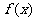 的单调增区间;
的单调增区间;
(Ⅱ)若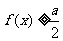 对任意
对任意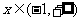 恒成立,求实数
恒成立,求实数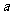 的取值范围.
的取值范围.
(21)(本小题满分12分)
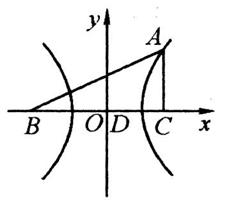
如图,直角坐标系xOy中,Rt△ABC中∠C=90°,B、C在x轴上且关于原点O对称,D在边BC上,BD=3DC,△ABC的周长为12.若一双曲线E以B、C为焦点,且经过A、D两点。
(1)求双曲线的方程;
(2)若过点P(m,0)(m为非零常数)的直线L与双曲线E相交于不同于双曲线顶点的两点M、N,且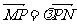 ,问x轴上是否存在定点G,使
,问x轴上是否存在定点G,使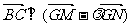 ?若存在,求出所有这样定点G的坐标;若不存在,请说明理由。
?若存在,求出所有这样定点G的坐标;若不存在,请说明理由。
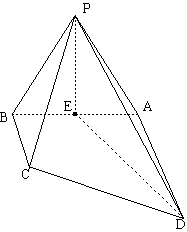
19.(本小题满分12分) 如图,四棱锥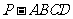 中,底面
中,底面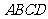 是直角梯形,
是直角梯形, ,
,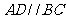 ,
,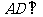 侧面
侧面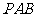 ,△
,△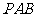 是等边三角形,
是等边三角形,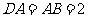 ,
,
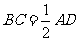 ,
,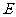 是线段
是线段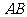 的中点.
的中点.
 (Ⅰ)求证:
(Ⅰ)求证: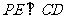 ;
;
(Ⅱ)求四棱锥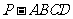 的体积;
的体积;
(Ⅲ)求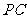 与平面
与平面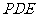 所成角的正弦值.
所成角的正弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com