
29.α1-抗胰蛋白缺乏症是一种在北美较为常见的单基因遗传病,患者成年后会出现肺气肿及其他疾病,严重者甚至死亡。
(1)下图为某患者及其家族部分成员系谱图,请据图回答问题:

根据图中 号个体即可半判断该遗传病的致病基因位于 染色体上。若图中Ⅲ1号个体携带致病基因,则致病基因可能来源于Ⅰ代中 号个体。若Ⅱ6号个体为该基因显性纯合子,Ⅲ2号个体携带致病基因的概率是 。
(2)对于该致病患者常可采用注射人α1-抗胰蛋白酶来缓解症状。利用转基因技术将控制该酶合成的基因导入羊的受精卵,最终培育出能在乳腺细胞表达人α1-抗胰蛋白酶的转基因羊,从而更易获得这种酶。下面表示获得转基因羊的简要过程。
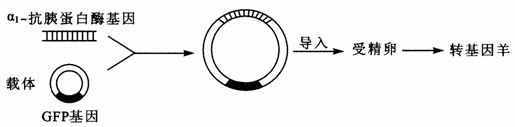
①获得目的基因后,常利用 技术在体外将其大量扩增。
②载体上绿色荧光蛋白(GFP)基因的作用是便于 。
③若要使转基因羊的后代均保持其特有的型号性状,理论上应选用 技术进行繁殖。
5.镰刀形细胞贫血症由基因突变引起,其致病基因为隐性基因(用a表示)。只有隐性纯合子才会发病,携带a基因的个体不发病,且对疟疾具有一定的抵抗力。在非洲某些地区,大约500人中就有20人患镰刀形细胞贫血症。因此在该地区人群中
A.a基因的基因频率大约为32%左右
B.a基因频率的变化是环境选择的结果
C.患者的死亡会导致人群中基因发生变化
D.a基因的携带者在自然选择中会逐渐被淘汰
第Ⅱ卷
4.右图是动物精子形成过程中某一时期的模式图,下列说法称确定是
A.如果分裂时3和4不分离,则产生的精细胞中染色体数目均异常
B.若在复制时没有发生如何差错,则该细胞能产生4种类型的精细胞
C.若染色体1和2发生部分片段的交换,则减数分裂无法正常进行
D.如图基因N发生突变,则该细胞产生的精细胞有一半出现异常
3.在气候条件适宜的情况下,弃耕的农田经过若干年后能演替成森林。在这一演替过程中
A.群落的优势种未发生明显的变化
B.群落中营养级的数目将逐渐增加
 C.认为因素是引起群落内部变化的根本原因
C.认为因素是引起群落内部变化的根本原因
D.各种信息沿着食物链中的营养级进行传递
2. 人体在某种条件改变时,内环境中一些物质的含量会发生相应变化。右图中的曲线可表示
人体在某种条件改变时,内环境中一些物质的含量会发生相应变化。右图中的曲线可表示
A.血糖降低时胰岛素含量的变化
B.缺碘引起甲状腺激素含量的变化
C.饮水过多时抗利尿激素含量的变化
D.再次感染甲流病毒后相关抗体含量的变化
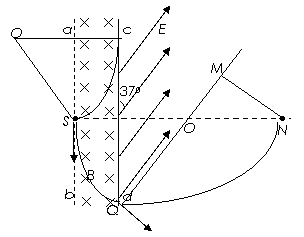
3. 如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q = 3.2×10-19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°=
0.8)求:
如图所示,真空室内存在宽度为d=8cm的匀强磁场区域,磁感应强度B=0.332T,磁场方向垂直于纸面向里;ab、cd足够长,cd为厚度不计的金箔,金箔右侧有一匀强电场区域,电场强度E=3.32×105N/C;方向与金箔成37°角.紧挨边界ab放一点状α粒子放射源S,可沿纸面向各个方向均匀放射初速率相同的α粒子,已知:α粒子的质量m=6.64×10-27kg,电荷量q = 3.2×10-19C,初速度v = 3.2×106m/s。(sin37°= 0.6,cos37°=
0.8)求:
(1)α粒子在磁场中作圆周运动的轨道半径R;
(2)金箔cd被α粒子射中区域的长度L;
(3)设打在金箔上d端离cd中心最远的α粒子穿出金箔进入电场,在电场中运动通过N点,SN⊥ab且SN = 40cm,则此α粒子从金箔上穿出时,损失的动能△EK为多少?
 解:(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即
解:(1)α粒子在匀强磁场中做匀速圆周运动,洛伦兹力提供向心力,即  (1分)
(1分)
则 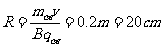 (2分)
(2分)
(2)设cd中心为O,向c端偏转的α粒子,当圆周轨迹与cd相切时偏离O最远,设切点为P,对应圆心O1,如图所示,则由几何关系得:
 (1分)
(1分)
向d端偏转的α粒子,当沿sb方向射入时,偏离O最远,设此时圆周轨迹与cd交于Q点,对应圆心O2,如图所示,则由几何关系得:
 (1分)
(1分)
故金箔cd被α粒子射中区域的长度 (1分)
(1分)
(3)设从Q点穿出的α粒子的速度为v′,因半径O2Q∥场强E,则v′⊥E,故穿出的α粒子在电场中做类平抛运动,轨迹如图所示。
沿速度v′方向做匀速直线运动, 位移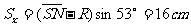 (1分)
(1分)
沿场强E方向做匀加速直线运动,位移 (1分)
(1分)
则由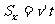

 得:
得: 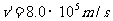 (2分)
(2分)
故此α粒子从金箔上穿出时,损失的动能为
 (2分)
(2分)
2.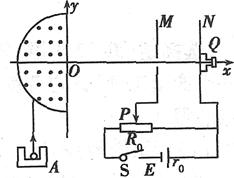 如图所示,某放射源A中均匀地向外辐射出平行于y轴的速度一定的α粒子,粒子质量为m,电荷量为q.为测定其从放射源飞出的速度大小,现让α粒子先经过一个磁感应强度为B、区域为半圆形的匀强磁场,经该磁场偏转后,它恰好能够沿x轴进入右侧的平行板电容器,并打到置于板N的荧光屏上出现亮点.当触头P从右端向左移动到滑动变阻器的中央位置时,通过显微镜头Q看到屏上的亮点恰好能消失.已知电源电动势为E,内阻为r0,滑动变阻器的总电阻R0=2 r0,求:
如图所示,某放射源A中均匀地向外辐射出平行于y轴的速度一定的α粒子,粒子质量为m,电荷量为q.为测定其从放射源飞出的速度大小,现让α粒子先经过一个磁感应强度为B、区域为半圆形的匀强磁场,经该磁场偏转后,它恰好能够沿x轴进入右侧的平行板电容器,并打到置于板N的荧光屏上出现亮点.当触头P从右端向左移动到滑动变阻器的中央位置时,通过显微镜头Q看到屏上的亮点恰好能消失.已知电源电动势为E,内阻为r0,滑动变阻器的总电阻R0=2 r0,求:
(1) α粒子从放射源飞出速度的大小 ;
;
(2)满足题意的α粒子在磁场中运动的总时间t;
(3)该半圆形磁场区域的半径R.

|
|||||||
|
|||||||
|
|||||||
 |
1. 如图甲所示,x轴正方向水平向右,y轴正方向竖直向上。在xoy平面内有与y轴平行的匀强电场,在半径为R的圆形区域内加有与xoy平面垂直的匀强磁场。在坐标原点O处放置一带电微粒发射装置,它可以连续不断地发射具有相同质量m、电荷量q(
如图甲所示,x轴正方向水平向右,y轴正方向竖直向上。在xoy平面内有与y轴平行的匀强电场,在半径为R的圆形区域内加有与xoy平面垂直的匀强磁场。在坐标原点O处放置一带电微粒发射装置,它可以连续不断地发射具有相同质量m、电荷量q(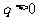 )和初速为
)和初速为 的带电粒子。已知重力加速度大小为g。
的带电粒子。已知重力加速度大小为g。
(1)当带电微粒发射装置连续不断地沿y轴正方向发射这种带电微粒时,这些带电微粒将沿圆形磁场区域的水平直径方向离开磁场,并继续沿x轴正方向运动。求电场强度和磁感应强度的大小和方向。
(2)调节坐标原点。处的带电微粒发射装置,使其在xoy平面内不断地以相同速率v0沿不同方向将这种带电微粒射入第1象限,如图乙所示。现要求这些带电微粒最终都能平行于x轴正方向运动,则在保证匀强电场、匀强磁场的强度及方向不变的条件下,应如何改变匀强磁场的分布区域?并求出符合条件的磁场区域的最小面积。
解:(1)由题目中“带电粒子从坐标原点O处沿y轴正方向进入磁场后,最终沿圆形磁场区域的水平直径离开磁场并继续沿x轴正方向运动”可知,带电微粒所受重力与电场力平衡。设电场强度大小为E,由平衡条件得:
 1分
1分
∴ 1分
1分
电场方向沿 轴正方向
轴正方向
带电微粒进入磁场后,做匀速圆周运动,且圆运动半径r=R。
设匀强磁场的磁感应强度大小为B。由牛顿第二定律得:
 1分
1分
∴ 1分
1分
磁场方向垂直于纸面向外 1分
(2)设由带电微粒发射装置射入第Ⅰ象限的带电微粒的初速度方向与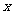 轴承夹角
轴承夹角 ,
,
则 满足0≤
满足0≤ ,由于带电微粒最终将沿
,由于带电微粒最终将沿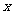 轴正方向运动,
轴正方向运动,
故B应垂直于 平面向外,带电微粒在磁场内做半径为
平面向外,带电微粒在磁场内做半径为 匀速圆周运动。
匀速圆周运动。
由于带电微粒的入射方向不同,若磁场充满纸面,
它们所对应的运动的轨迹如图所示。 2分
为使这些带电微粒经磁场偏转后沿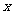 轴正方向运动。
轴正方向运动。
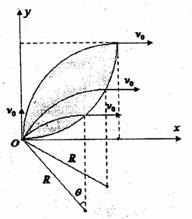 由图可知,它们必须从经O点作圆运动的各圆的最高点飞离磁场。
由图可知,它们必须从经O点作圆运动的各圆的最高点飞离磁场。
这样磁场边界上P点的坐标P(x,y)应满足方程:
 ,
,
 ,
,
所以磁场边界的方程为:
 2分
2分
由题中0≤ 的条件可知,
的条件可知,
以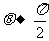 的角度射入磁场区域的微粒的运动轨迹
的角度射入磁场区域的微粒的运动轨迹

即为所求磁场的另一侧的边界。 2分
因此,符合题目要求的最小磁场的范围应是圆
 与圆
与圆 的
的
交集部分(图中阴影部分)。 1分
由几何关系,可以求得符合条件的磁场的最小面积为:
 1分
1分
20.根据下面这首小诗,展开想象,将该诗扩写为一段80字左右的文字。
古池
古池畔,青蛙一轻跃,水叮咚。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
七、作文(60分) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com