
3.设有一个直线回归方程为
 ,则变量x 增加一个单位时 ( )
,则变量x 增加一个单位时 ( )
A. y 平均增加 1.5 个单位 B. y 平均增加 2 个单位
C. y 平均减少 1.5 个单位 D. y 平均减少 2 个单位
2.线性回归方程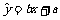 表示的直线必经过的一个定点是( )
表示的直线必经过的一个定点是( )
A.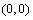 B.
B.
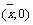 C.
C.
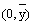 D.
D.
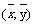
1.下表是某小卖部一周卖出热茶的杯数与当天气温的
对比表:若热茶杯数y与气温x近似地满足线性关系,
则其关系式最接近的是( )
A.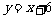 B.
B.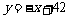 C.
C.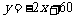 D.
D.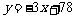
21.高三年级1000名学生进行数学其中测试。高三年级组随机调阅了100名学生的试卷(满分为150分),成绩记录如下:
|
成绩(分) |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人数 |
6 |
8 |
10 |
15 |
15 |
35 |
8 |
3 |
求样本平均数和样本方差.
 必修3
第2章
统计
必修3
第2章
统计
§2.4线性回归方程
重难点:散点图的画法,回归直线方程的求解方法,回归直线方程在现实生活与生产中的应.
考纲要求:①会作两个有关联变量数据的散点图,会利用散点图认识变量间的相关关系.
②了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.
经典例题:10.有10名同学高一(x)和高二(y)的数学成绩如下:
|
高一成绩x |
74 |
71 |
72 |
68 |
76 |
73 |
67 |
70 |
65 |
74 |
|
高二成绩y |
76 |
75 |
71 |
70 |
76 |
79 |
65 |
77 |
62 |
72 |
⑴画出散点图;
⑵求y对x的回归方程。
当堂练习:
|
气温/℃ |
18 |
13 |
10 |
4 |
-1 |
|
杯数 |
24 |
34 |
39 |
51 |
63 |
20.有一组数据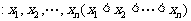 的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11.
的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11.
(1) 求出第一个数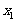 关于
关于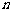 的表达式及第
的表达式及第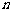 个数
个数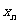 关于
关于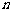 的表达式.
的表达式.
(2)若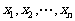 都是正整数,试求第
都是正整数,试求第 个数
个数 的最大值,并举出满足题目要求且
的最大值,并举出满足题目要求且 取到最大值的一组数据.
取到最大值的一组数据.
19.在参加世界杯足球赛的32支球队中,随机抽取20名队员,调查其年龄为25,21,23,25,27,29,25,28,30,29,26,24,25,27,26,22,24,25,26,28。填写下面的频率分布表,据此估计全体队员在哪个年龄段的人数最多?占总数的百分之几?并画出频率分布直方图.
|
分组 |
频数 |
频率 |
|
20.5-22.5 |
|
|
|
22.5-24.5 |
|
|
|
24.5-26.5 |
|
|
|
26.5-28.5 |
|
|
|
28.5-30.5 |
|
|
|
合计 |
|
|
18.(1)完成上面的频率分布表.
(2)根据上表,画出频率分布直方图.
(3)根据上表,估计数据落在[10.95,11.35]范围内的概率约为多少?
17.数据a1,a2,a3,…,an的方差为σ2,平均数为μ,则数据ka1+b,ka2+b,ka3+b,…,kan+b(kb≠0)的标准差为 ,平均数为 .
16.期中考试以后,班长算出了全班40个人数学成绩的平均分为M,如果把M当成一个同学的分数,与原来的40个分数一起,算出这41个分数的平均值为N,那么M:N为 .
|
分组 |
频数 |
频率 |
|
[10.75,10.85] |
3 |
|
|
[10.85,10.95] |
9 |
|
|
[10.95,11.05] |
13 |
|
|
[11.05,11.15] |
16 |
|
|
[11.15,11.25] |
26 |
|
|
[11.25,11.35] |
20 |
|
|
[11.35,11.45] |
7 |
|
|
[11.45,11.55] |
4 |
|
|
[11.55,11.65] |
2 |
|
|
合计 |
100 |
|
15.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com