
19.(本小题满分12分) 如图,四棱锥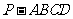 中,底面
中,底面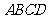 是直角梯形,
是直角梯形,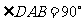 ,
,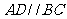 ,
,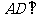 侧面
侧面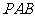 ,△
,△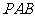 是等边三角形,
是等边三角形,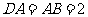 ,
,
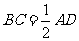 ,
,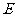 是线段
是线段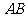 的中点.
的中点.
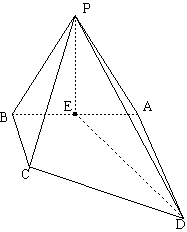 (Ⅰ)求证:
(Ⅰ)求证: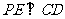 ;
;
(Ⅱ)求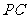 与平面
与平面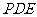 所成角的正弦值.
所成角的正弦值.
18.(本小题满分12分)
某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试. 假设某学生每次通过测试的概率都是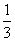 ,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否互相独立. 规定:若前4次都没有通过测试,则第5次不能参加测试.
(Ⅰ) 求该学生考上大学的概率.
(Ⅱ) 如果考上大学或参加完5次测试就结束,记该生参加测试的次数为ξ,求P( )
)
17. (本小题满分12分)已知函数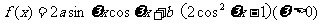 在
在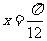 时取最大值2。
时取最大值2。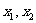 是集合
是集合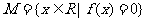 中的任意两个元素,|
中的任意两个元素,| |的最小值为
|的最小值为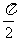 。
。
(I)求a、b的值;
(II)若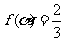 ,求
,求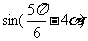 的值。
的值。
16、给出定义:若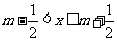 (其中
(其中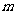 为整数),则
为整数),则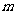 叫做离实数
叫做离实数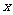 最近的整数,记作
最近的整数,记作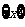 ,即
,即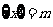 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数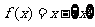 的四个命题:
①
的四个命题:
①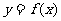 的定义域是
的定义域是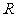 ,值域是
,值域是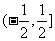 ;
;
②点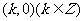 是
是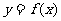 的图像的对称中心;
的图像的对称中心;
③函数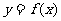 的最小正周期为1;
的最小正周期为1;
④ 函数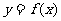 在
在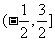 上是增函数;
上是增函数;
则其中真命题是__ .
15、设曲线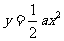 在点
在点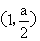 处的切线与直线
处的切线与直线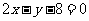 平行,又已知圆
平行,又已知圆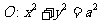 和点
和点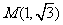 ,则过点M且与圆O相切的直线与两坐标轴围成的三角形的面积等于_____________
,则过点M且与圆O相切的直线与两坐标轴围成的三角形的面积等于_____________
14、在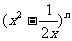 的展开式中只有第
的展开式中只有第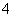 项的二项式系数最大,则第
项的二项式系数最大,则第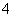 项的系数是
.(用数字作答)
项的系数是
.(用数字作答)
13、设等比数列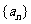 的前
的前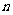 项和为
项和为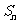 ,且
,且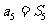 ,则
,则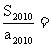 _____________.
_____________.
12、定义在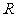 上的函数
上的函数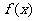 满足数列
满足数列 ,当
,当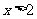 时,
时,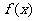 单调递增。如果
单调递增。如果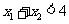 ,且
,且 ,则
,则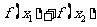 的值 ( )
的值 ( )
A.恒大于0 B. 恒小于0 C.可能为0 D.可正可负
第Ⅱ卷
11、已知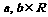 ,若关于
,若关于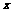 的方程
的方程 的实根
的实根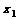 和
和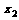 满足-1≤
满足-1≤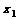 ≤1,1≤
≤1,1≤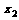 ≤2,则在平面直角坐标系aOb中,点(
≤2,则在平面直角坐标系aOb中,点(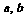 )所表示的区域内的点P到曲线
)所表示的区域内的点P到曲线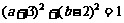 上的点Q的距离|PQ|的最小值为
( )
上的点Q的距离|PQ|的最小值为
( )
A. 2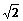 +1 B.2
+1 B.2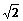 -1 C. 3
-1 C. 3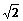 +1 D.3
+1 D.3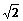 -1
-1
10、已知有穷数列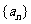
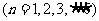 满足
满足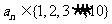 ,且当
,且当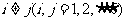 时
时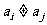 。若
。若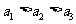 ,
,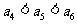 ,则符合条件的数列
,则符合条件的数列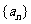 的个数是( )
的个数是( )
A.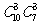 B.
B.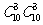 C.
C.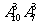 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com