
5. 已知正项等差数列{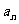 },满足
},满足 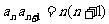 ,则{
,则{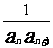 }的前n项和为( )
}的前n项和为( )
A.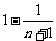 B.
B. 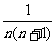 C.
C. 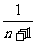 D.
D.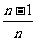
4.已知椭圆C.: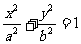 以抛物线
以抛物线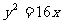 的焦点为焦点,且短轴一个端点与两个焦点可组成一个等边三角形,那么椭圆C.的离心率
的焦点为焦点,且短轴一个端点与两个焦点可组成一个等边三角形,那么椭圆C.的离心率 为 ( )
为 ( )
A.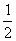 B.
B.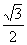 C.
C. 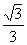 D.
D. 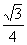
3.用0.1.2.3.4这五个数字组成无重复数字的五位数,其中奇数的个数是 ( )
A. 18 B. 24 C.36 D. 48
2.已知集合M={x︱x=y2},N={x︱x2-x-2>0},U=R,则 = ( )
= ( )
A.{x︱0<X≤2} B.{x︱0≤X<2}
C.{x︱0≤X≤2} D.{x︱0<X<2}
1.复数 运算结果是 ( )
运算结果是 ( )
A.4
B.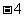 C.
C. D.
D.
22、(本题14分)
已知函数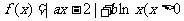 ,实数a,b为常数),
,实数a,b为常数),
(1)若a=1,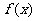 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程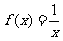 在(0,1]上解的个数。
在(0,1]上解的个数。
21、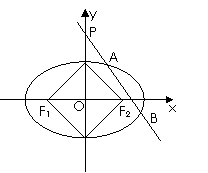 (本题12分)已知中心为坐标原点O,焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形,
(本题12分)已知中心为坐标原点O,焦点在x轴上的椭圆的两个短轴端点和左右焦点所组成的四边形是面积为2的正方形,
(1)求椭圆的标准方程;
(2)过点P(0,2)的直线l与椭圆交于点A,B,
当△OAB面积最大时,求直线l的方程。
20、(本题12分)已知数列{an}的前n项和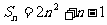 ,数列{bn}满足b1+3b2+…+(2n-1)bn=(2n―3)·2n+1,
,数列{bn}满足b1+3b2+…+(2n-1)bn=(2n―3)·2n+1,
求:数列{anbn}的前n项和Tn。
19、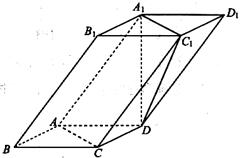 (本题12分)如图,四棱柱ABCD-A
(本题12分)如图,四棱柱ABCD-A B
B C
C D
D 中,A
中,A D
D 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA =2.
=2.
(1)求证:C D∥平面ABB
D∥平面ABB A
A ;
;
(2)求直线BD 与平面A
与平面A C
C D所成角的正弦值;
D所成角的正弦值;
(3)求二面角D-A C
C 一A的余弦值.
一A的余弦值.
18、(本题12分)某种家电器每台的销售利润与该电器无故障使用时间T(单位:年)有关,若T≤1,则销售利润为0元,若1<T≤3,则销售利润为100元,若T>3,则销售利润为200元,设每台该种电台无故障使用时间T≤1,1<T≤3及T>3这三种情况发生的概率为为P1,P2,P3,又知P1,P2是方程25x2-15x+a=0的两个根,且P2=P3,
(1)求P1,P2,P3的值;
(2)记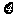 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求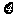 的分布列;
的分布列;
(3)求销售两台这种家用电器的销售利润总和的平均值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com