2．在植物细胞工程中，当原生质体融合成一个细胞后，需要诱导产生出细胞壁，参与这一过程的细胞器是(　　　 )

A．叶绿体、高尔基体　 　　　　　　　　　 B．线粒体、高尔基体

C．叶绿体、线粒体　　　　　　　　　　　 D．线粒体、内质网

1、利用动物细胞融合技术制各单克隆抗体时，需要将抗原注射到小鼠体内，注射后的小鼠血液中可能获得新的(　　　 )

①B淋巴细胞 ②T淋巴细胞 ③记忆细胞 ④效应B细胞 ⑤效应T细胞 ③抗体

A．①②⑤⑥　　 B．②③⑤⑥　 C．①③④⑥　　 D．③④⑤⑥

22. (本题满分12分)已知数列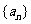满足：.

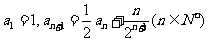　 (1)求数列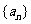的通项公式；

　 (2)证明：；

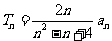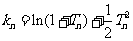　 (3)设，且，证明：.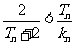

21. (本题满分12分)设椭圆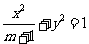的两个焦点是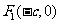与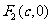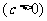，且椭圆上存在点M，使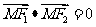. (1)求实数m 的取值范围；

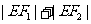　 (2)若直线与椭圆存在一个公共点E，使得取得最小值，求此最小值及此时椭圆的方程；

　 (3)在条件(2)下的椭圆方程，是否存在斜率为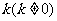的直线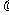，与椭圆交于不同的两点A、B，满足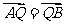，且使得过点Q，N(0，－1)两点的直线NQ满足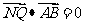？若存在，求出k的取值范围；若不存在，说明理由.

20. (本题满分12分)某种商品的成本为5元/ 件，开始按8元/件销售，销售量为50件，为了获得最大利润，商家先后采取了提价与降价两种措施进行试销。经试销发现：销售价每上涨1元每天销售量就减少10件；而降价后，日销售量Q(件)与实际销售价x(元)满足关系：

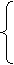
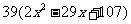
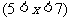
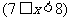
　(1)求总利润(利润＝销售额－成本)y(元)与销售价x(件)的函数关系式；

　(2)试问：当实际销售价为多少元时，总利润最大.

19. (本题满分12分)如图，在直三棱柱ABC－A₁B₁C₁中，

AC⊥BC，AC＝BC＝CC₁，D为AB的中点.　　　　　　　　

　 (1)求证：AC₁∥平面CDB₁；

　 (2)求二面角B－B₁C－D的余弦值的大小.

18. (本题满分12分)下面玩掷骰子放球游戏，若掷出1点或6点，甲盒放一球；若掷出2点，3点，4点或5点，乙盒放一球，设掷n次后，甲、乙盒内的球数分别为x、y.

　 (1)当n=3时，求x=3，y=0的概率；

　 (2)当n=4时，设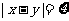，求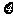的分布列及数学期望E.

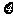17. (本题满分10分)已知函数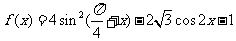，且给定条件“”.　

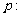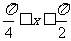(1)求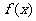的最大值及最小值；

(2)若又给条件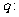“”且p是q的充分条件，求实数m的取值范围.

16. 在三角形ABC中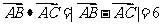，，M为BC边的中点，则中线AM的长为　　　　　　　 . △ABC的面积的最大值为　　　　　　 .

15. 如图是一几何体的平面展开图，其中ABCD为正方形，E、F分别为PA、PD的中点，在此几何体中，给出下面四个结论：

　 1直线BE与直线CF异面；

　 2直线BE与直线AF异面；

　 3直线EF∥平面PBC；

　 4平面BCE⊥平面PAD.

　 其中正确的有　　　　　 个.