
5.(2010年江苏卷物理15).(16分)制备纳米薄膜装置的工作电极可简化为真空中间距为d的两平行极板,如图甲所示.加在极板A、B间的电压UAB作周期性变化,其正向电压为U0,反向电压为-kU0(k>1),电压变化的周期为2r,如图乙所示.在t=0时,极板B附近的一个电子,质量为m,电荷量为e,受电场作用由静止开始运动.若整个运动过程中,电子未碰到极板A,且不考虑重力作用.
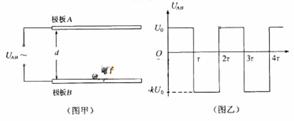
(1)若k=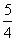 ,电子在0-2t时间内不能到达极板A,求d应满足的条件;
,电子在0-2t时间内不能到达极板A,求d应满足的条件;
(2)若电子在0-200t时间内未碰到极板B、求此运动过程中电子速度v随时间t变化的关系;
(3)若电子在第N个周期内的位移为零,求k的值.
解:(1)电子在0~f时间内做匀加速运动
加速度的大小 a1=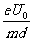 ①
①
位移x1=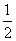 a1T2 ②
a1T2 ②
在T-2T时间内先做匀减速运动,后反向做匀加速运动
加速度的大小 a2=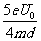 ③
③
初速度的大小 v1=a1r ④
匀减速运动阶段的位移x2=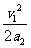 ⑤
⑤
依据题意 d>x1+x2
解得d>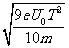 ⑥
⑥
(2)在2nr~(2n+1)r,(n=0,1,2, ……,99)时间内⑦
加速度的大小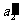 2=
2=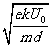
速度增量△v2=-a′2r ⑧
(a)当0≤t-2nt<r时
电子的运动速度 v=n△v1+n△v2+a1(t-2nT)⑨
解得v=[t-(k+1)nr] 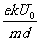 ,(n=0,1,2, ……,99)⑩
,(n=0,1,2, ……,99)⑩
(b)当0≤t-(2n+1)r<T时
电子的运动速度 v=(n+1)
△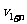 △v2-a′2[t-(2n+1)r] 11
△v2-a′2[t-(2n+1)r] 11
解得v=[(n+1)(k+1)r-kt]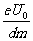 ,(n=0,1,2, ……,99)12
,(n=0,1,2, ……,99)12
(3)电子在2(N-1)r~(2N-1)r时间内的位移x2N-1=v2N-2r+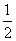 a1r2
a1r2
电子在(2N-1)r~2NT时间内的位移x2N=v2N-1r-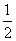 a′2r2
a′2r2
由10式可知v2N-2=(N-1)(1-k)r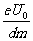
由12式可知v2N-1=(N-Nk+k)r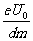
依据题意x2N-1+x2N=0
解得k=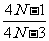
4.(2010年江苏卷物理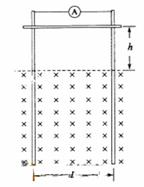 13).(15分)如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
13).(15分)如图所示,两足够长的光滑金属导轨竖直放置,相距为L,一理想电流表与两导轨相连,匀强磁场与导轨平面垂直.一质量为m、有效电阻为R的导体棒在距磁场上边界h处静止释放.导体棒进入磁场后,流经电流表的电流逐渐减小,最终稳定为I.整个运动过程中,导体棒与导轨接触良好,且始终保持水平,不计导轨的电阻.求:
(1)磁感应强度的大小B;
(2)电流稳定后,导体棒运动速度的大小v;
(3)流以电流表电流的最大值Im.
解:(1)电流稳定后,导体棒做匀速运动 BIL=mg ①
解得 B=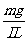 ②
②
(2)感应电动势E=BLv ③
感应电流 I=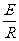 ④
④
由②③④式解得 v=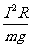
(3)由题意知,导体棒刚进入磁场时的速度最大,设为vm
机械能守恒 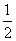 mv
mv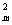 =mgh
=mgh
感应电动势的最大值 Em=BLvm
感应电流的最大值 Im=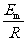
解得 Im=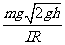
3.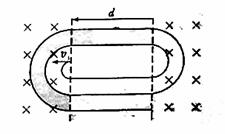 (2010年山东卷25).(18分)如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为
(2010年山东卷25).(18分)如图所示,以两虚线为边界,中间存在平行纸面且与边界垂直的水平电场,宽度为 ,两侧为相同的匀强磁场,方向垂直纸面向里。一质量为
,两侧为相同的匀强磁场,方向垂直纸面向里。一质量为 ,带电量
,带电量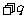 ,重力不计的带电粒子,以初速度
,重力不计的带电粒子,以初速度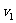 垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求
垂直边界射入磁场做匀速圆周运动,后进入电场做匀加速运动,然后第二次进入磁场中运动,此后粒子在电场和磁场中交替运动。已知粒子第二次在磁场中运动的半径是第一次的二倍,第三次是第一次的三倍,以此类推。求
(1)粒子第一次经过电场的过程中电场力所做的功W1。
(2)粒子第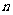 次经过电场时电场强度的大小
次经过电场时电场强度的大小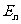 。
。
(3)粒子第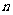 次经过电场所用的时间
次经过电场所用的时间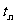 。
。
(4)假设粒子在磁场中运动时,电场区域场强为零。请画出从粒子第一次射入磁场至第三次离开电场的过程中,电场强度随时间变化的关系图线(不要求写出推导过程,不要求标明坐标刻度值)。

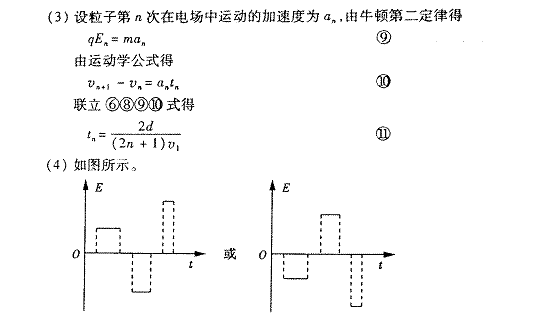
2.(2010年全国II卷26).(21分)
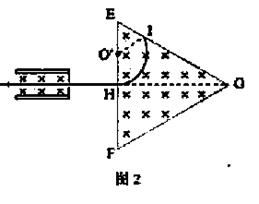
 图中左边有一对平行金属板,两板相距为d,电压为v;两版之间有匀强磁场,磁感应强度大小为B0,方向平行于板面并垂直于纸面朝里。图中右边右边有一边长为a的正三角形区域EFG(EF边为金属板垂直)在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。
图中左边有一对平行金属板,两板相距为d,电压为v;两版之间有匀强磁场,磁感应强度大小为B0,方向平行于板面并垂直于纸面朝里。图中右边右边有一边长为a的正三角形区域EFG(EF边为金属板垂直)在此区域内及其边界上也有匀强磁场,磁感应强度大小为B,方向垂直于纸面朝里。假设一系列电荷量为q的正离子沿平行金属板面、垂直于磁场的方向射入金属板之间,沿同一方向射出金属板之间的区域,并经EF边中点H射入磁场区域。不计重力。
(1)已知这些离子中的离子甲到达磁场边界EG后,从边界EF穿出磁场,求离子甲的质量。
(2)已知离子中的离子乙从EG边上1点(图中未画出)穿出磁场,且GI长为3/4a,求离子乙的质量。
(3)若这些离子中的最轻离子的质量等于离子甲质量的一半,而离子乙的质量是最大的,问磁场边界上区域内可能有离子到达。
解:(1)由题意知,所有离了在平行金属板之间做匀速直线运动,它所受到的向上的磁场力和向下的电场力平衡,有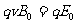 ①
①
式中,v是离子运动的速度,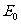 是平行金属板之间的匀强电场的强度,有
是平行金属板之间的匀强电场的强度,有
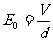 ②
②
由①②式得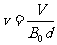 ③
③
在正三角形磁场区域,离子甲做匀速圆周运动,设郭子甲质量为m,由洛仑兹力公式和牛顿第二定律有
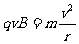 ④
④
式中,r是离子甲做圆周运动的半径,离子甲在磁场中的运动轨迹为半圆,圆心为O,这半圆刚好与EG边相切于K点,与EF边交于P点。在△EOK中,OK垂直于EG。由几保关系得
 ⑤
⑤
由⑤式得
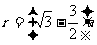 ⑥
⑥
联立③④⑥式得,离子甲的质量为
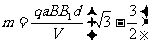 ⑦
⑦
(2)同理,由洛仑兹力公式和牛顿第二定律有
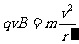 ⑧
⑧
式中, 分别为离子乙的质量和做圆周运动的轨道半径,离子乙运动的圆周的圆心O必在E、H两点之间。由几何关系有
分别为离子乙的质量和做圆周运动的轨道半径,离子乙运动的圆周的圆心O必在E、H两点之间。由几何关系有
 ⑨
⑨
由⑨式得
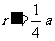 ⑩
⑩
联立③⑧⑩式得,离子乙的质量为
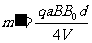 11
11
(3)对于最轻的离子,其质量为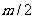 ,
,
由④式知,它在磁场中做半径为
的匀速圆周运动,因而与EH的交点
为O,有
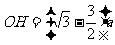 12
12
当这些离子中的离子质量逐渐增大到 时,离子到达磁场边界上的点的位置从O点沿HE边变到P点:当离子质量继续增大时,离子到达磁场边界上的点的位置从K点沿EG边趋向于1点。K点到G点的距离为
时,离子到达磁场边界上的点的位置从O点沿HE边变到P点:当离子质量继续增大时,离子到达磁场边界上的点的位置从K点沿EG边趋向于1点。K点到G点的距离为
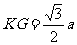 13
13
所以,磁场边界上可能有离子到达的区域是:EF边上从O到P,EG边上从K到1。
1.(2010年全国I卷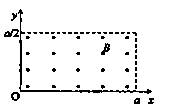 25).(18分)
25).(18分)
如图所示,在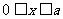 、
、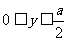 范围内有垂
范围内有垂
直于 平面向外的匀强磁场,磁感应强度大小为
平面向外的匀强磁场,磁感应强度大小为
B。坐标原点O处有一个粒子源,在某时刻发射大
量质量为m、电荷量为 的带正电粒子,它们的速
的带正电粒子,它们的速
度大小相同,速度方向均在 平面内,与
平面内,与 轴正方向的夹角分布在0-90°范围内。已知粒子在磁场中做圆周运动的半径介于
轴正方向的夹角分布在0-90°范围内。已知粒子在磁场中做圆周运动的半径介于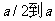 之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子从粒子源射出时的
之间,从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一。求最后离开磁场的粒子从粒子源射出时的
(1)速度的大小;
(2)速度方向与 轴正方向夹角的正弦。
轴正方向夹角的正弦。
解:(1)设粒子的发射速度为 ,粒子做圆周运动的轨道半径为R,由牛顿第二定律和洛仑兹力公式,得
,粒子做圆周运动的轨道半径为R,由牛顿第二定律和洛仑兹力公式,得
 ①
①
由①式得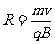 ②
②
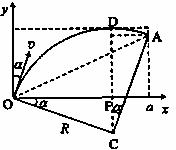 当
当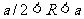 时,在磁场中运动时间最长的粒子,
时,在磁场中运动时间最长的粒子,
其轨迹是圆心为C的圆弧,圆弧与磁场的上边界相切,
如右图所示,设该粒子在磁场运动的时间为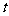 ,
,
依题意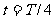 ,
,
得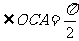 ③
③
设最后离开磁场的粒子的发射方向与 轴正方向
轴正方向
的平角为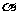 ,由几何关系可得
,由几何关系可得
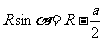 ④
④
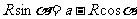 ⑤
⑤
又
由④⑤⑥式得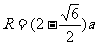 ⑦
⑦
由②⑦式得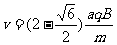 ⑧
⑧
(2)由④⑦式得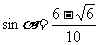 ⑨
⑨
15.(四川卷)下列说法正确的是
A.α粒子大角度散射表明α粒子很难进入原子内部
B.氢原子跃迁发出的光从空气射入水时可能发生全反射
C.裂变反应有质量亏损,质量数不守恒
D.γ射线是一种波长很短的电磁波
答案:D
解析:α粒子的散射学习现象表明大多数α粒子不发生偏转,说明穿过了原子,少数α粒子发生偏转,说明无法穿过原子核,A错误。任何光只有在从光密介质进入光疏介质时才能发生全反射,B错误。裂变有质量亏损是因为核子的平均密度变化引起的,但是核子的总数并未改变,C错误。γ射线是频率很大波长很短的电磁波。D正确。
1.(天津卷)下列关于电磁波的说法正确的是
A.均匀变化的磁场能够在空间产生电场
B.电磁波在真空和介质中传播速度相同
C.只要有电场和磁场,就能产生电磁波
D.电磁波在同种介质中只能沿直线传播
答案:A
7.(上海物理)
电磁波包含了 射线、红外线、紫外线、无线电波等,按波长由长到短的排列顺序是
射线、红外线、紫外线、无线电波等,按波长由长到短的排列顺序是
(A)无线电波、红外线、紫外线、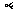 射线
射线
(B)红外线、无线电波、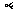 射线、紫外线
射线、紫外线
(C)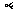 射线、红外线、紫外线、无线电波
射线、红外线、紫外线、无线电波
(D)紫外线、无线电波、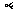 射线、红外线
射线、红外线
答案:A
解析:本题考查电磁波普。
难度:易。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com