
3.3.在△ABC中,D、E、F分别BC、CA、AB的中点,点M是△ABC的重心,则
 等于 ( )
等于 ( )
A. B.
B. C.
C. D.
D.
2.设 ,而
,而 是一非零向量,则下列各结论:①
是一非零向量,则下列各结论:① ;②
;②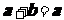 ;③
;③ ;④
;④ ,其中正确的是
( )
,其中正确的是
( )
A.①② B.③④ C.②④ D.①③
1. 、
、 为非零向量,且
为非零向量,且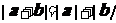 ,则
( )
,则
( )
A. 与
与 方向相同 B.
方向相同 B.


C.

 D.
D. 与
与 方向相反
方向相反
12.如图,中国象棋的半个棋盘上有一只“马”,开始下棋时,它位于A点,这只“马”第一步有几种可能的走法?试在图中画出来.若它位于图中的P点,这只“马”第一步有几种可能的走法?它能否从点A走到与它相邻的B?它能否从一交叉点出发,走到棋盘上的其它任何一个交叉点?
 必修4
第2章 平面向量
必修4
第2章 平面向量
§2.2向量的线性运算
重难点:灵活运用向量加法的三角形法则和平行四边形法则解决向量加法的问题,利用交换律和结合律进行向量运算;灵活运用三角形法则和平行四边形法则作两个向量的差,以及求两个向量的差的问题;理解实数与向量的积的定义掌握实数与向量的积的运算律体会两向量共线的充要条件.
考纲要求:①掌握向量加法,减法的运算,并理解其几何意义.
②掌握向量数乘的运算及其意义。理解两个向量共线的含义.
③了解向量线性运算的性质及其几何意义.
 经典例题:如图,已知点
经典例题:如图,已知点 分别是
分别是 三边
三边 的中点,
的中点,
求证: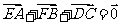 .
.
.
当堂练习:
11. 如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,
如图,△ABC中,D,E,F分别是边BC,AB,CA的中点,在以A、B、C、D、E、F为端点的有向线段中所表示的向量中,
(1)与向量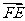 共线的有
.
共线的有
.
(2)与向量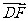 的模相等的有
.
的模相等的有
.
(3)与向量 相等的有
.
相等的有
.
10.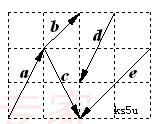 在如图所示的向量
在如图所示的向量 ,
, ,
, ,
, ,
, 中(小正方形的边长为1),是否存在:
中(小正方形的边长为1),是否存在:
(1)是共线向量的有 ;
(2)是相反向量的为 ;
(3)相等向量的的 ;
(4)模相等的向量 .
9. O是正六边形ABCDE的中心,且
O是正六边形ABCDE的中心,且 ,
, ,
, ,在以A,B,C,D,E,O为端点的向量中:
,在以A,B,C,D,E,O为端点的向量中:
(1)与 相等的向量有
;
相等的向量有
;
(2)与 相等的向量有
;
相等的向量有
;
(3)与 相等的向量有
相等的向量有
8.如图,O是正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形,在图中所示的向量中:
(1)与 相等的向量有
;
相等的向量有
;
(2)写出与 共线的向有
;
共线的向有
;
(3)写出与 的模相等的有
;
的模相等的有
;
(4)向量 与
与 是否相等?答
.
是否相等?答
.
7. 在①平行向量一定相等;②不相等的向量一定不平行;③共线向量一定相等;④相等向量一定共线;⑤长度相等的向量是相等向量;⑥平行于同一个向量的两个向量是共线向量中,不正确的命题是
.并对你的判断举例说明
.
在①平行向量一定相等;②不相等的向量一定不平行;③共线向量一定相等;④相等向量一定共线;⑤长度相等的向量是相等向量;⑥平行于同一个向量的两个向量是共线向量中,不正确的命题是
.并对你的判断举例说明
.
6.已知O是正方形ABCD对角线的交点,在以O,A,B,C,D这5点中任意一点为起点,另一点为终点的所有向量中,
(1)与 相等的向量有
;
相等的向量有
;
(2)与 长度相等的向量有
;
长度相等的向量有
;
(3)与 共线的向量有
.
共线的向量有
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com