
1.若向量a=(1,1),b=(1,-1),c=(-1,2),则c等于 ( )
A.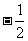 a
a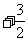 b B.
b B.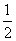 a
a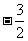 b C.
b C.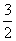 a
a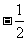 b D.
b D.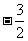 a+
a+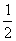 b
b
12.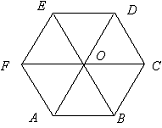 如图在正六边形ABCDEF中,已知:
如图在正六边形ABCDEF中,已知: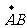 =
= ,
, 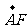 =
=  ,试用
,试用 、
、 表示向量
表示向量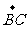 ,
, 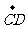 ,
, 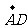 ,
,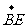 .
.
 必修4
第2章
平面向量
必修4
第2章
平面向量
§2.3平面向量的基本定理及坐标表示
重难点:对平面向量基本定理的理解与应用;掌握平面向量的坐标表示及其运算.
考纲要求:①了解平面向量的基本定理及其意义.
②掌握平面向量的正交分解及其坐标表示.
③会用坐标表示平面向量的加法,减法于数乘运算.
④理解用坐标表示的平面向量共线的条件.
经典例题:已知点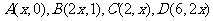 .
.
求实数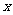 的值,使向量
的值,使向量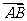 与
与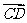 共线;
共线;
当向量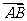 与
与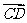 共线时,点
共线时,点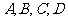 是否在一条直线上?
是否在一条直线上?
当堂练习:
11.一汽车向北行驶3 km,然后向北偏东60 方向行驶3 km,求汽车的位移.
方向行驶3 km,求汽车的位移.
10.若向量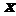 、
、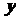 满足
满足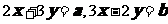 ,
,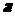 、
、 为已知向量,则
为已知向量,则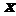 =__________;
=__________;
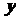 =___________.
=___________.
9.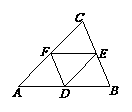 如图,D、E、F分别是
如图,D、E、F分别是 ABC边AB、BC、CA上的
ABC边AB、BC、CA上的
中点,则等式:
①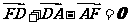 ②
②
③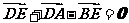 ④
④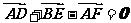
8.当非零向量 和
和 满足条件
时,使得
满足条件
时,使得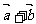 平分
平分 和
和 间的夹角。
间的夹角。
7.已知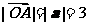 ,
,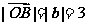 ,∠AOB=60
,∠AOB=60 ,则
,则 __________。
__________。
6.已知四边形ABCD是菱形,点P在对角线AC上(不包括端点A、C),则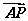 =
=
( )
A.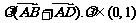 B.
B.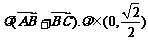
C. 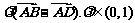 D.
D.
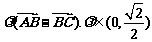
5.若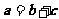 化简
化简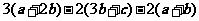 ( )
( )
A. B.
B. C.
C. D.
以上都不对
D.
以上都不对
4.已知向量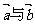 反向,下列等式中成立的是 ( )
反向,下列等式中成立的是 ( )
A.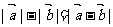 B.
B.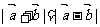
C.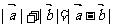 D.
D.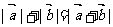
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com