

9.若| |=2,|
|=2,| |=
|=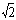 ,
, 与
与 的夹角为45°,要使k
的夹角为45°,要使k -
- 与
与 垂直,则k=
垂直,则k=
8.已知 =(1,-1),
=(1,-1), =(-2,1),如果(
=(-2,1),如果(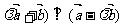 ,则实数
,则实数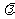 = 。
= 。
7.已知点A(1,0),B(3,1),C(2,0)则向量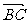 与
与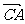 的夹角是
。
的夹角是
。
6.已知 =(m-2,m+3),
=(m-2,m+3), =(2m+1,m-2)且
=(2m+1,m-2)且 与
与 的夹角大于90°,则实数m( )
的夹角大于90°,则实数m( )
A、m>2或m<-4/3 B、-4/3<m<2 C、m≠2 D、m≠2且m≠-4/3
5.有下面四个关系式(1)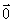 ·
·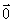 =
=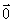 ;(2)(
;(2)( ·
· )
)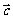 =
= (
( ·
·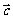 );(3)
);(3) ·
· =
= ·
· ;(4)0
;(4)0 =0,其中正确的个数是
( )
=0,其中正确的个数是
( )
A、4 B、3 C、2 D、1
4.已知 =(3,-1),
=(3,-1), =(1,2),向量
=(1,2),向量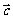 满足
满足 ·
·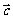 =7,且
=7,且
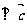 ,则
,则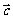 的坐标是( )
的坐标是( )
A.(2,-1) B、(-2,1) C、(2,1) D、(-2,-1)
3.已知 =(2,3),
=(2,3), =(-4,7)则向量
=(-4,7)则向量 在
在 方向上的投影为
( )
方向上的投影为
( )
A.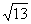 B、
B、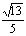 C、
C、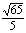 D、
D、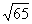
2.已知 =(1,-2),
=(1,-2), =(5,8),
=(5,8),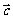 =(2,3),则
=(2,3),则 ·(
·( ·
·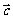 )的值为
( )
)的值为
( )
A.34 B、(34,-68) C、-68 D、(-34,68)
1.已知 =(3,0),
=(3,0), =(-5,5)则
=(-5,5)则 与
与 的夹角为
( )
的夹角为
( )
A.450 B、600 C、1350 D、1200
12.如果向量 =i-2j,
=i-2j,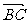 =i+mj,其中i、j分别是x轴、y轴正方向上的单位向量,
=i+mj,其中i、j分别是x轴、y轴正方向上的单位向量,
试确定实数m的值使A、B、C三点共线.
 必修4
第2章
平面向量
必修4
第2章
平面向量
§2.4平面向量的数量积
重难点:理解平面向量的数量积的概念,对平面向量的数量积的重要性质的理解.
考纲要求:①理解平面向量数量积的含义及其物理意义.
②了解平面向量数量积于向量投影的关系.
③掌握数量积的坐标表达式,会进行平面向量数量积的运算.
④能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.
经典例题:在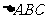 中,设
中,设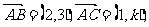 且
且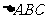 是直角三角形,求
是直角三角形,求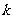 的值.
的值.
当堂练习:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com