
1、设a=0.3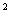 ,b=2
,b=2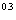 ,c=log
,c=log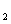
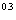 则它们的大小关系为( )
则它们的大小关系为( )
A.c<a<b B.a<c<b C.a<b<c D.b<c<a
22.(本小题满分12分)设等比数列{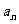 }的前
}的前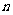 项和
项和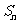 ,首项
,首项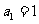 ,公比
,公比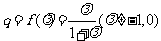 .
.
(Ⅰ)证明: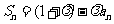 ;
;
(Ⅱ)若数列{ }满足
}满足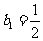 ,
,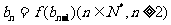 ,求数列{
,求数列{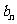 }的通项公式;
}的通项公式;
(Ⅲ)若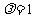 ,
,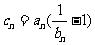 ,数列{
,数列{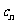 }
} 的前项和为
的前项和为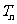 ,求证:当
,求证:当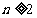 时,
时,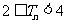 .
.
2010年普通高等学校招生全国统一考试预测试卷
21.(本小题满分12分)已知椭圆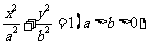 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线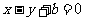 是抛物线
是抛物线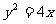 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点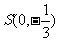 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
20.(本小题满分12分)已知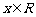 ,函数
,函数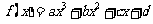 在
在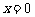 处取得极值,曲线
处取得极值,曲线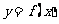 过原点
过原点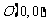 和点
和点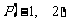 .若曲线
.若曲线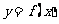 在点
在点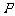 处的切线
处的切线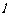 与直线
与直线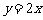 的夹角为
的夹角为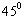 ,且直线
,且直线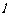 的倾斜角
的倾斜角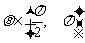
(Ⅰ)求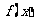 的解析式;
的解析式;
(Ⅱ)若函数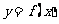 在区间
在区间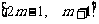 上是增函数,求实数
上是增函数,求实数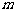 的取值范围;
的取值范围;
(Ⅲ)若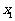 、
、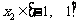 ,求证:
,求证: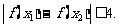
19.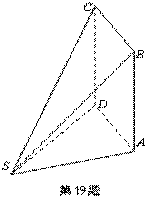 (本小题满分12分)如图,多面体AB
(本小题满分12分)如图,多面体AB CDS中,面ABCD为矩形,
CDS中,面ABCD为矩形, 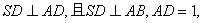
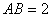 ,
, 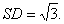
(I)求证 :CD
:CD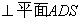 ;
;
(II)求AD与SB所成角的余弦值;
(III)求二面角A-SB-D的余弦值.
18.(本题满分12分)有关部门要了解甲型H1N1流感预防知识在学校的普及情况,命制了一份有10道题的问卷到各学校做问卷调查.某中学A,B两个班各被随机抽取5名学生接受问卷调查,A班5名学生得分为:5、8、9、9、9;B班5名学生得分为:6,7,8,9,10.
(Ⅰ)请你估计A,B两个班中哪个班的问卷得分要稳定一些;
(Ⅱ)如果把B班5名学生的得分看成一个总体,并用简单随机抽样方法从中抽取样本容量为2的 样本,求样本平均数与总体平均数之差的绝对值不小于1的概率.
样本,求样本平均数与总体平均数之差的绝对值不小于1的概率.
17.(本小题满分10分)已知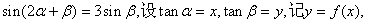
(Ⅰ)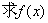 的解析表达式;
的解析表达式;
(Ⅱ)若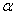 角是一个三角形的最小内角,试求函数
角是一个三角形的最小内角,试求函数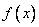 的值域.
的值域.
16.给出下列命题:
A.函数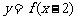 和
和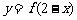 的图象关于直线
的图象关于直线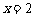 对称.
对称.
B.已知函数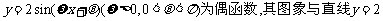 的交点的横坐标为
的交点的横坐标为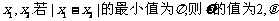 的值为
的值为 .
.
C.底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.
D.若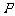 为双曲线
为双曲线 上的一点,
上的一点,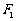 、
、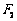 分别为双曲线的左右焦点,且
分别为双曲线的左右焦点,且 ,则
,则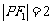 或
或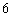 .
.
其中正确的命题是 (把所有正确的命题的选项都填上 )
)
15.写出“函数f (x)=x2+2ax+1(a∈R)在区间(1,+∞)上是增函数”成立的一 个充分不必要条件:_________.
个充分不必要条件:_________.
14.一个六棱柱的底面是正六边形,其侧棱垂直底面.已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为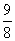 ,底面周长为3,则这个球的体积为 .
,底面周长为3,则这个球的体积为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com