
8.空间四边形ABCD中, AC=AD, BC=BD, 则AB与CD所成的角为( )
A. 300 B. 450 C. 600 D. 900
7.下面条件中, 能判定直线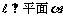 的一个是( )
的一个是( )
A. 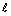 与平面
与平面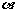 内的两条直线垂直
B.
内的两条直线垂直
B. 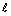 与平面
与平面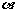 内的无数条直线垂直
内的无数条直线垂直
C. 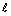 与平面
与平面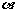 内的某一条直线垂直 D.
内的某一条直线垂直 D.
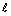 与平面
与平面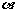 内的任意一条直线垂直
内的任意一条直线垂直
6. 直线a,b是异面直线,则下列结论成立的是( )
A. 过不在a,b上的任意一点,可作一个平面与a,b平行
B. 过不在a,b上的任意一点,可作一条直线与a,b相交
C. 过不在a,b上的任意一点,可作一条直线与a,b都平行
D. 过a可以并且只可以作一个平面与b平行
5.直线a,b是异面直线,A是不在a,b上的点,则下列结论成立的是( )
A. 过A有且只有一个平面平行于a,b B. 过A至少有一个平面平行于a,b
C. 过A有无数个平面平行于a,b D. 过A且平行于a,b的平面可能不存在
4.下无命题中正确的是( )
①过一点, 一定存在和两条异面直线都平行的平面; ②垂直于同一条直线的一条直线和一个平面平行; ③若两条直线没有公共点, 则过其中一条直线一定有一个平面与另一条直线平行.
A. ① B. ③ C. ①③ D. ①②③
3.下列命题正确的个数是( )
①若直线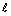 上有无数个点不在平面
上有无数个点不在平面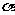 内, 则
内, 则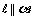 ; ②若直线
; ②若直线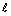 与平面
与平面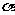 平行, 则
平行, 则 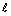 与平面
与平面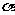 内有任意一条直线都平行; ③如果两条平行直线中的一条直线与一个平面平行, 那么另一条直线也与这个平面平行; ④若直线
内有任意一条直线都平行; ③如果两条平行直线中的一条直线与一个平面平行, 那么另一条直线也与这个平面平行; ④若直线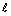 与平面
与平面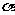 平行, 则
平行, 则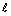 与平面
与平面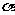 内的任意一条直线都没有公共点.
内的任意一条直线都没有公共点.
A.0个 B. 1个 C. 2个 D.3个
2.直线b是平面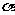 外的一条直线,下列条件中可得出b||
外的一条直线,下列条件中可得出b||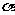 的是( )
的是( )
A.b与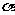 内的一条直线不相交 B.b与
内的一条直线不相交 B.b与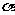 内的两条直线不相交
内的两条直线不相交
C.b与 内的无数条直线不相交 D.b与
内的无数条直线不相交 D.b与 内的所有直线不相交
内的所有直线不相交
1.下面命题正确的是 ( )
A.若直线与平面不相交,则这条直线与这个平面没有公共点
B.若直线与平面不相交,则这条直线与这个平面内的任何一条直线没有公共点
C.若一条直线与一个平面有公共点,直线与这相交
D.直线在平面外,则直线与平面相交或平行
21.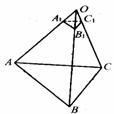 在共点O的三条不共面直线a、b、c上,在点O的同侧分别取点A的A1、B的B1、C和C1,使得
在共点O的三条不共面直线a、b、c上,在点O的同侧分别取点A的A1、B的B1、C和C1,使得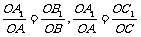 .
.
求证:  ∽
∽ A1B1C1 .
A1B1C1 .
 必修2
必修2
第1章 立体几何初步
§1.2.3 直线与平面的位置关系
重难点:了解直线与平面的位置关系,在判定和证明直线与平面的位置关系时,除了能熟练运用判定定理和性质定理外,还要充分利用定义;线面关系的判定和证明,要注意线线关系、线面关系的转化.
 经典例题:直角
经典例题:直角 ABC所在平面外一点S,且SA=SB=SC.
ABC所在平面外一点S,且SA=SB=SC.
⑴求证:点S与斜边中点D的 连线SD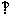 面ABC;
面ABC;
⑵若直角边BA=BC,求证:BD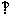 面SAC.
面SAC.
当堂练习:
20. 如图,已知空间四边形ABCD的对角线AC=14cm,BD=14cm,M,N分别是AB,CD的中点,MN=7
如图,已知空间四边形ABCD的对角线AC=14cm,BD=14cm,M,N分别是AB,CD的中点,MN=7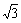 cm,
cm,
求异面直线AC与BD所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com