
6.正方体的全面积是a2,它的顶点都在球面上,这个球的表面积是( )
A. B.
B. C.
C. D.
D. 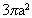 7.两个球的表面积之差为48
7.两个球的表面积之差为48 ,它们的大圆周长之和为12
,它们的大圆周长之和为12 ,这两个球的半径之差为( )
,这两个球的半径之差为( )
A.4 B. 3 C. 2 D. 1
5.三个球的半径之比为1:2:3,那么最大球的表面积是其余两个球的表面积之和的( )
A.1倍
B.2倍
C.1 倍 D.1
倍 D.1 倍
倍
4.球的大圆面积扩大为原大圆面积的4倍,则球的表面积扩大成原球面积的( )
A.2倍 B. 4倍 C. 8倍 D.16倍
3.边长为5cm的正方形EFGH是圆柱的轴截面, 则从E点沿圆柱的侧面到相对顶点G的最短距离是( )
A. 10cm
B. 5 cm
C. 5
cm
C. 5 cm D.
cm D. cm
cm
2.若球的半径为R,则这个球的内接正方体的全面积等于( )
A.8R2 B. 9R2 C.10R2 D.12R2
1.长方体ABCD-A1B1C1D1的AB=3,AD=2,CC1=1,一条绳子从A沿着表面拉到点C1,绳子的最短长度是( )
A.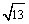 +1 B.
+1 B.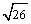 C.
C. D.
D.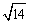
21.如果两个相交平面都和第三个平面垂直,那么它们的交线也和第三个平面垂直.
 必修2
第1章
立体几何初步
必修2
第1章
立体几何初步
§1.3柱、锥、台、球的表面积和体积
考纲要求:了解柱、锥、台、球的表面积和体积的计算公式(不要求记忆公式);会求一些简单几何体的表面积和体积,体会积分思想在计算表面积和体积的运用.
重难点:了解柱、锥、台、球的表面积和体积的计算公式,会求一些简单几何体的表面积和体积,体会积分思想在计算表面积和体积的运用.
经典例题:在三棱柱ABC-DEF中,已知AD到面BCFE的距离为h,平行四边形BCFE的面积为S.
求:三棱柱的体积V.
当堂练习:
20.如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周上不同于A、B的任意一点.
 求证:平面PAC垂直于平面PBC.
求证:平面PAC垂直于平面PBC.
19. 如图,平面 ,线段AB分别交
,线段AB分别交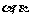 于M、N,线段AD分别交
于M、N,线段AD分别交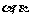 于C、D,线段BF分别交
于C、D,线段BF分别交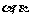 于F、E,若AM=9,MN=11,NB=15,S
于F、E,若AM=9,MN=11,NB=15,S =78.求
=78.求 END的面积.
END的面积.
18.已知a和b是两条异面直线,求证过a而平行于b的平面 必与过b而平行于a的平面
必与过b而平行于a的平面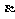 平行.
平行.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com