8．(2010年北京卷22)(16分)

　　　 如图，跳台滑雪运动员经过一段加速滑行后从O点水平飞出，经过3．0 s落到斜坡上的A点。已知O点是斜坡的起点，斜坡与水平面的夹角＝37°，运动员的质量m＝50 kg。不计空气阻力。(取sin37°＝0．60，cos37°＝0．80;g取10 m/s²)求

　 　 (1)A点与O点的距离L;

　 (2)运动员离开O点时的速度大小;

　 (3)运动员落到A点时的动能。

解：(1)运动员在竖直方向做自由落体运动，有

A点与O点的距离

　 (2)设运动员离开O点的速度为V。运动员在水平方向做匀速直线运动，

即　　

解得　 　m/s

　 (3)由机械能守恒，取A点为重力势能零点，运动员落到A点时的动能为

6．(2010年江苏卷物理14)(16分)

在游乐节目中，选手需借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论．如图所示，他们将选手简化为质量m=60 kg 的质点，选手抓住绳由静止开始摆动，此时绳与竖直方向夹角＝53°，绳的悬挂点O距水面的高度为H＝3 m．不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深．取重力加速度

　 (1)求选手摆到最低点时对绳拉力的大小F；

　 (2)若绳长l=2 m，选手摆到最高点时松手落入水中．设水对选手的平均浮力f₁=800N,平均阻力f₂=700N，求选手落入水中的深度d；

(3)若选手摆到最低点时松手，小明认为绳越长，在浮台上的落点距岸边越远；小阳却认为绳越短，落点距岸边越远．请通过推算说你的观点．

解：(1)机械能守恒mgl(1－cos)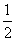＝mv²　　　　　　　　　　　 ①

　　　 圆周运动F′－mg＝m

　　　 解得F′＝(3－2cos)mg

　　　 人对绳的拉力F＝F′

　　　 则F＝1080N

　 (2)动能定理　 mg(H－lcos+d)－(f₁+f₂)d＝0

　　　 则d==1.2m　　　　　　　　　

　　　 (3)选手从最低点开始做平抛运动x=vt

　　　 H-l=

　　　 且有①式

　　　 解得x=2

　　　 当l=时，x有最大值　　　　　　　　　　　　　 解得l=1．5m

　　　 因此，两人的看法均不正确．当绳长越接近1．5m时，落点距岸边越远．

　 7．(2010年天津卷10)(16分)

如图所示，小球A系在细线的一端，线的另一端固定在O点,O点到水平面的距离为h。物块B质量是小球的5倍，置于粗糙的水平面上且位于O点正下方，物块与水平面间的动摩擦因数为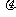。现拉动小球使线水平伸直，小球由静止开始释放，运动到最低点时与物块发生正碰(碰撞时间极短)，反弹后上升至最高点时到水平面的距离为。小球与物块均视为质点，不计空气阻力，重力加速度为g，求物块在水平面上滑行的时间t。

解：设小球的质量为m，运动到最低点与物块碰撞前的速度大小为，取小球运动到最低点重力势能为零，根据机械能守恒定律，有

　　　 　　 ①

　　　 得

　　　 设碰撞后小球反弹的速度大小为，同理有

　　　 　 ②

　　　 得

　　　 设碰后物块的速度大小为，取水平向右为正方向，根据动量守恒定律，有

　　　 　 ③

　　　 得　　　　 ④

　　　 物块在水平面上滑行所受摩擦力的大小 　⑤

　　　 设物块在水平面上滑行的时间为t，根据动量定理，有　 ⑥

　　　 得　　 ⑦

5．(2010年山东卷24)(15分) 如图所示，四分之一圆轨道与水平轨道相切，它们与另一水平轨道在同一竖直面内，圆轨道的半径R=0.45m，水平轨道长=3m, 与均光滑。一滑块从O点由静止释放，当滑块经过A点时，静止在CD上的小车在F=1.6N的水平恒力作用下启动，运动一段时间后撤去力F。当小车在CD上运动了=3.28m时速度v=2.4m/s,此时滑块恰好落入小车中。已知小车质量M=0.2,与CD间的动摩擦因数=0.4。(取g=10m/)求

(1)恒力F的作用时间t。

(2)与的高度差h。

4．(2010年全国II卷25)．(18分)

小球A和B的质量分别为m_A和m_B，且 m_A >m_B 。在某高度处将A和B先后从静止释放。小球A与水平面碰撞后向上弹回，在释放处下方与释放处距离为H的地方恰好与正在下落的小球B发生正碰。设所有碰撞都是弹性的，碰撞时间极短。求小球A、B碰撞后上升的B最大高度。

解：根据题意，由运动学规律可知，小球A与B碰撞前的速度大小相等，设均为v₀。由机械能守恒有

　　 ①

设小球A与B碰撞后的速度分别为v₁和v₂，以竖直向上方向为正，由动量守恒有

　　 ②

由于两球碰撞过程中能量守恒，故

　　　　　 ③

联立②③式得

④

设小小球B能上升的最大高度为，由运动学公式有

⑤

由①④⑤式得

⑥

3．(2010年全国II卷24)．(15分)

如图，MNP为竖直面内一固定轨道，其圆弧段MN与水平NP相切于N，P端固定一竖直板。M相对于N的高度为h，NP长度为s．衣物快自M端从静止开始沿轨道下滑，与挡板发生一次完全弹性碰撞后停止在水平轨道上某处。若在MN段的摩擦可忽略不计，物块与NP段轨道间的滑动摩擦因数为　μ　，求物块停止的地方与N点距离的可能值。

解：根据功能关系，在物块从开始下滑到静止的过程中，物块重力势能减小的数值AE_P与物块克服摩擦力所做功的数值W相等，即

△E_P=W　　　　　 ①

设物块质量为m，在水平轨道上滑行的总路程为s′，则

△E_p=mgh　　　　　 ②

W=μmgs′　　　　 ③

设物块在水平轨道上停 住的地方与N点的距离为d，若物块在与P碰撞垢，在到达圆弧形轨道停止，则

s′=2s－d　　　　　 ④

联立①②③④式得

　　　　 ⑤

此结果在时有效，若，则物块在与P碰撞后，可再一次滑上圆弧形轨道。滑下后在水平轨道上停止，此时有

　　　　　 s′=2s+d　　　　　 ⑥

联立①②③⑥式得

2.(2010年安徽卷22)(14分)

　　　 质量为2kg的物体水平推力F的作用下溶水平面做直线运动。一段时间后撤去F,其运动的v-t图象如图所示。g取10m/s²，求；

　 (1)物体与水平间的动摩擦因数μ;

　 (2)水平推力F的大小;

　 (3)0-10s内物体运动位移的大小。

解：(1)设物体做匀速直线运动的时间为、初速度为、未速度为、加速度为，则　　　 ①

设物体所受的摩擦力为，根据牛顿第二定律，有

　　　　　　　　　　　　　　　　　　　　　　　 ②

　　　　　　　　　　　　　　　　　　　　　 ③

联立②③得

　　　　　　　　　　　　　　　　　　　 ④

　 (2)设物体估做匀加速运动的时间为，初速度为、末速度为、加速度为，

则　　　　　　　　　　　 ⑤

根据牛顿第二定律，有

　　　　　　　　　　　　　　　　　　　　 ⑥

联立③⑥得

1．(2010年全国I卷24)．(14分)

短跑名将博尔特在北京奥运会上创造了100m和200m短路项目的新世界纪录，他的成绩分别是96.9s和19.30s。假定他在100m比赛时从发令到起跑的反应时间是0.15s起跑后做匀加速运动，达到最大速率后做匀速运动。200m比赛时，反应时间及起跑后加速阶段的加速度时间与100m比赛时相同，但由于弯道和体力等因素的影响，以后的平均速率只有跑100m时最大速率的96%。求：

　 (1)加速所用时间和达到的最大速率；

　 (2)起跑后做匀加速运动的加速度。(结果保留两位小数)

解：(1)设加速所用时间为t(以s为单位)，匀速运动的速度为(以m/s为单位)则有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

　　　 　　　　　　　　　　　　　　　　　 ②

　　　 由①②式得

　　　 t=1.29s　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

　 (2)设加速度大小为，则　 　　　　　　　　　　 ⑤

20．(安徽卷)如图所示，水平地面上方矩形区域内存在垂直纸面向里的匀强磁场，两个边长相等的但匝闭合正方形线圈Ⅰ和Ⅱ，分别用相同材料，不同粗细的导线绕制(Ⅰ为细导线)。两线圈在距磁场上界面高处由静止开始自由下落，再进入磁场，最后落到地面。运动过程中，线圈平面始终保持在竖直平面内且下边缘平行于磁场上边界。设线圈Ⅰ、Ⅱ落地时的速度大小分别为、，在磁场中运动时产生的热量分别为、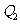。不计空气阻力，则

A．　　　　　　　 B．　　　　　

C．　　　　　　　 D．

答案：D

解析：由于从同一高度下落，到达磁场边界时具有相同的速度v，切割磁感线产生感应电流同时受到磁场的安培力，又(ρ为材料的电阻率，l为线圈的边长)，所以安培力，此时加速度，且 (为材料的密度)，所以加速度是定值，线圈Ⅰ和Ⅱ同步运动，落地速度相等v₁ =v₂。由能量守恒可得：，(H是磁场区域的高度)，Ⅰ为细导线m小，产生的热量小，所以Q₁< Q₂。正确选项D。

24.(四川卷)(19分)如图所示，电源电动势。内阻，电阻。间距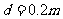的两平行金属板水平放置，板间分布有垂直于纸面向里、磁感应强度的匀强磁场。闭合开关，板间电场视为匀强电场，将一带正电的小球以初速度沿两板间中线水平射入板间。设滑动变阻器接入电路的阻值为R_x，忽略空气对小球的作用，取。

(1)当R_x=29Ω时，电阻消耗的电功率是多大？

(2)若小球进入板间做匀速圆周运动并与板相碰，碰时速度与初速度的夹角为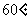，则R_x是多少？

[答案]⑴0.6W；⑵54Ω。

[解析]⑴闭合电路的外电阻为

　　　 Ω　　　　　　　 ①

　 根据闭合电路的欧姆定律

　　　 A　　　　　　　　　　　　　　 ②

　 R₂两端的电压为

　　　 V　　　　　　　　 ③

　 R₂消耗的功率为

　　　 W　　　　　　　　　　　　　　　　 ④

⑵小球进入电磁场做匀速圆周运动，说明重力和电场力等大反向，洛仑兹力提供向心力，根据牛顿第二定律

　　　 　　　　　　　　　　　　　　　　　　　　　⑤

　　　 　　　　　　　　　　　　　　　　　　　　　⑥

　 连立⑤⑥化简得

　　　 　　　　　　　　　　　　　　　　　　　　　⑦

　 小球做匀速圆周运动的初末速的夹角等于圆心角为60°，根据几何关系得

　　　 　　　　　　　　　　　　　　　　　　　　　　　　⑧

　 连立⑦⑧带入数据

　　　 V

　 干路电流为

　　　 　A　　　　　　　　　　　　　　　　 ⑨

　　　 Ω　　　　　　　　　　 ⑩

23.(重庆卷)(16分)法拉第曾提出一种利用河流发电的设想，并进行了实验研究。实验装置的示意图可用题23图表示，两块面积均为S的矩形金属板，平行、正对、竖直地全部浸在河水中，间距为d。水流速度处处相同，大小为v，方向水平。金属板与水流方向平行。

地磁场磁感应强度的竖直分量为B，水的电阻为p，水面上方有一阻值为R的电阻通过绝缘导线和电建K连接到两金属板上。忽略边缘效应，求：

(1)该发电装置的电动势；

(2)通过电阻R的电流强度；

(3)电阻R消耗的电功率。

解析：

(1)由法拉第电磁感应定律，有

(2)两板间河水的电阻

由闭合电路欧姆定律，有

(3)由电功率公式，

得