
5.若圆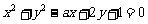 与圆
与圆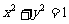 关于直线
关于直线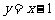 对称,过点
对称,过点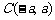 的圆P与
的圆P与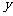 轴相切,则圆心P的轨迹方程为( )
轴相切,则圆心P的轨迹方程为( )
A.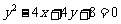 B.
B.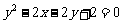
C.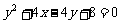 D.
D.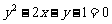
4.已知函数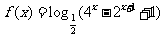 的值域是
的值域是 ,则它的定义域可以是( )
,则它的定义域可以是( )
A.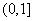 B.
B.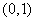 C.
C. D.
D.
3.函数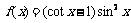 的最小正周期是( )
的最小正周期是( )
A.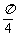 B.
B.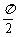 C.
C.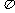 D.
D.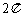
2.已知全集为U=R,集合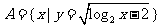 ,
,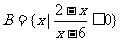 ,则
,则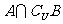 =( )
=( )
A.{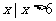 } B.
} B.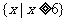 C.
C.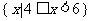 D.
D.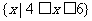
1.复数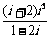 等于( )
等于( )
A.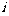 B.
B.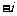 C.
C.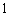 D.
D.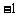
21.(本小题满分14分)
(1)选修4-2:矩阵与变换
已知矩阵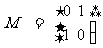 ,
,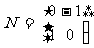 。在平面直角坐标系中,设直线
。在平面直角坐标系中,设直线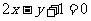 在矩阵
在矩阵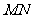 对应的变换作用下得到的曲线
对应的变换作用下得到的曲线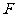 ,求曲线
,求曲线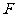 的方程。
的方程。
(2)选修4 - 4:坐标系与参数方程
在极坐标系中,已知圆C的圆心坐标为C (2,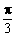 ),半径R=
),半径R=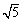 ,求圆C的极坐标方程
,求圆C的极坐标方程
(3)选修4-5:不等式选讲
已知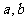 为正数,求证:
为正数,求证: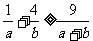
20. (本小题满分13分)
设函数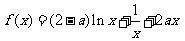 (
(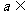 R).
R).
(Ⅰ)当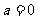 时,求
时,求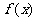 的极值;
的极值;
(Ⅱ)当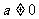 时,求
时,求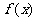 的单调区间;
的单调区间;
(Ⅲ)当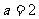 时,对于任意正整数
时,对于任意正整数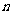 ,在区间
,在区间 上总存在
上总存在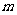 +4个数
+4个数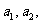
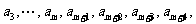 使得
使得
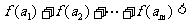
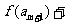
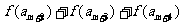 成立,试问:正整数
成立,试问:正整数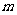 是否有最大值?若有求其最大值;否则,说明理由
是否有最大值?若有求其最大值;否则,说明理由
19. (本小题满分13分)
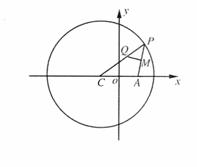
已知C为圆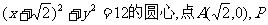 是圆上的动点,点Q在圆的半径CP上,且
是圆上的动点,点Q在圆的半径CP上,且
(Ⅰ)当点P在圆上运动时,求点Q的轨迹E的方程;
 (Ⅱ)一直线
(Ⅱ)一直线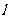 ,原点到
,原点到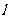 的距离为
的距离为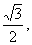
(1)求证直线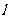 与曲线E必有两个交点
与曲线E必有两个交点
(2)若直线 与曲线E的两个交点分别为G、H,
与曲线E的两个交点分别为G、H,
求△OGH的面积的最大值
18.(本题满分13分)
如图,在三棱柱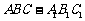 中,已知
中,已知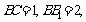
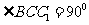 ,
,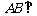 侧面
侧面
(1)求直线C1B与底面ABC所成角的正弦值;
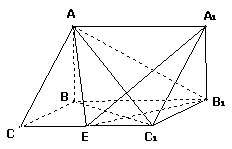 (2)在棱
(2)在棱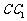 (不包含端点
(不包含端点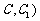 上确定一点
上确定一点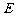 的位置,使得
的位置,使得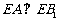 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若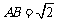 ,求二面角
,求二面角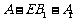 的大小.
的大小.
17. (本小题满分13分)
已知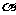 为锐角,且
为锐角,且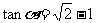 ,函数
,函数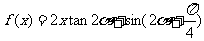 ,数列{
,数列{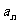 }的首项
}的首项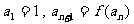
⑴ 求函数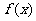 的表达式;
的表达式;
⑵ 求证:数列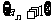 为等比数列;
为等比数列;
⑶ 求数列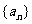 的前
的前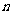 项和
项和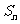
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com