(2010·苏北四市二联考)下图是“某区域地理环境演变示意图”。读图回答5-6题。

5．引起图中地理环境演变的原因是(双选)　　　　　　　　　　　　　　　　　　 (　)

A．大气环流　 　　　　　　B．海陆位置

C．地壳运动 　　　　　　D．地形的变化

6．图示地理环境的演变过程主要体现了(双选)　　　　　　　　　　　　　　　　 (　)

A．地理环境的差异性　 　　　　　B．地理环境的整体性

C．地理要素的联系性 　　　　　　D．地理要素的独立性

解析　第5题，从图中可以看出，该区域的大气环流(常年盛行风向)、海陆位置都没有

发生变化，排除AB选项；而地势却在逐渐升高，说明地壳在运动，故正确选项为CD。

第6题，从演变过程看，该区域的地形发生了变化，其他要素也跟着出现相应的变化，

如植被(森林减少，草地、荒漠出现)、降水(迎风坡降水多，背风坡形成雨影区)等，说明

地理环境各要素之间是有联系的，也充分说明地理环境是一个整体，故正确选项为BC。

答案　5.CD　6.BC

(2010·盐城二调)读漫画“把云留住”，完成3-4题。

3．与该漫画主题最贴切的环境问题是　　　　　　　　　　　　　　　　　　　　 (　)

A．土地盐碱化　 　　　　　B．大气污染

C．森林破坏　　　　 　　D．温室效应

4．此图体现了区域地理环境的　　　　　　　　　　　　　　　　　　　　　　 (　)

A．整体性　 　　　　　　B．差异性

C．开放性 　　　　　　　D．同一性

解析　第3题，漫画反映的主题是植被破坏导致区域内涵养水源能力下降，气候变干，

土地沙化更加严重。第4题，图中反映了植被破坏会引起降水减少、土地沙化、环境恶

化等问题，体现了区域地理环境的整体性特点，即“牵一发而动全身”。

答案　3.C　4.A

(2009·天津文综)读“某外流湖自然消亡过程示意图”，回答1-2题。

1．该湖泊自然消亡的原因，据图可以确定的是　　　　　　　　　　　　　　　　 (　)

A．地壳上升 　　　　　　　B．水源减少

C．气候变干 　　　　　　　D．物质沉积

2．湖泊消亡引起了湖区自然景观的变化，这反映了自然环境的　　　　　　　　　 (　)

A．整体性　 　　　　　　　B．差异性

C．稳定性 　　　　　　　　D．脆弱性

解析　第1题，从湖泊消亡过程图中可以看出，从第1幅图到第3幅图，湖泊周围的植

被明显减少，受其影响，水土流失可能会加剧；从第1幅图到第3幅图，湖泊深度越来

越浅，直到消亡。第2题，湖泊消亡引起湖区自然景观的变化体现了地理环境的整体性，

地理环境的某一要素发生变化，其他要素也会发生变化，即“牵一发而动全身”。

答案　1.D　2.A

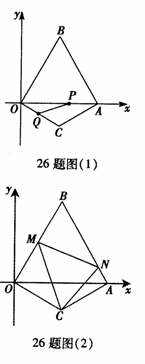
26．已知：如图(1)，在平面直角坐标xOy中，边长为2的等边△OAB的顶点B在第一象限，顶点A在x轴的正半轴上．另一等腰△OCA的顶点C在第四象限，OC＝AC，∠C＝120°．现有两动点P、Q分别从A、O两点同时出发，点Q以每秒1个单位的速度沿OC向点C运动，点P以每秒3个单位的速度沿A→O→B运动，当其中一个点到达终点时，另一个点也随即停止.

(1)求在运动过程中形成的△OPQ的面积S与运动的时间t之间的函数关系，并写出自变量t的取值范围；

(2)在等边△OAB的边上(点A除外)存在点D，使得△OCD为等腰三角形，请直接写出所有符合条件的点D的坐标；

(3)如图(2)，现有∠MCN＝60°，其两边分别与OB、AB交于点M、N，连接MN．将∠MCN绕着C点旋转(0°＜旋转角＜60°)，使得M、N始终在边OB和边AB上．试判断在这一过程中，△BMN的周长是否发生变化？若没有变化，请求出其周长；若发生变化，请说明理由．

25．今年我国多个省市遭受严重干旱，受旱灾的影响，4月份，我市某蔬菜价格呈上升趋势，其前四周每周的平均销售价格变化如下表：

进入5月，由于本地蔬菜的上市，此种蔬菜的平均销售价格y(元/千克)从5月第1周的2.8元/千克下降至第2周的2.4元/千克，且y与周数x的变化情况满足二次函数y＝－ x²+bx+c.

(1)请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识直接写出4月份y与x 的函数关系式，并求出5月份y与x的函数关系式；

(2)若4月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m＝x+1.2，5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m＝x+2．试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大？且最大利润分别是多少？

(3)若5月份的第2周共销售100吨此种蔬菜．从5月份的第3周起，由于受暴雨的影响，此种蔬菜的可供销量将在第2周销量的基础上每周减少a %，政府为稳定蔬菜价格，从外地调运2吨此种蔬菜，刚好满足本地市民的需要，且使此种蔬菜的销售价格比第2周仅上涨0.8 a %．若在这一举措下，此种蔬菜在第3周的总销售额与第2周刚好持平，请你参考以下数据，通过计算估算出a的整数值．

(参考数据：37²＝1369，38²＝1444，39²＝1521，40²＝1600，41²＝1681)

24． 已知：如图，在直角梯形ABCD中，AD∥BC，∠ABC＝90°．点E是DC的中点，过点E作DC的垂线交AB于点P，交CB的延长线于点M．点F在线段ME上，且满足CF＝AD，MF＝MA．

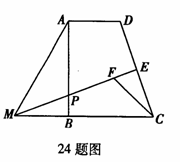(1)若∠MFC＝120°，求证：AM＝2MB；

(2)求证：∠MPB＝90°－ ∠FCM．

23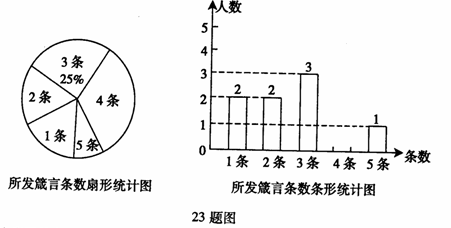．在“传箴言”活动中，某班团支部对该班全体团员在一个月内所发箴言条数的情况进行了统计，并制成了如下两幅不完整的统计图：

(1)求该班团员在这一个月内所发箴言的平均条数是多少？并将该条形统计图补充完整；

(2)如果发了3条箴的同学中有两位同学，发了4条箴言的同学中有三位女同学． 现要从发了3条箴和4条箴言的同学中分别选出一位参加该校团委组织的“箴言”活动总结会，请你用列表法或树状图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．

22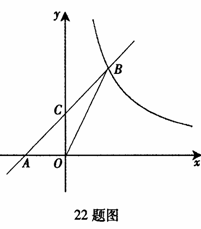．已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A(－2，0)，与反比例函数在第一象限内的图象的交于点B(2，n)，连结BO，若S_△AOB＝4．

(1)求该反比例函数的解析式和直线AB的解析式；

(2)若直线AB与y轴的交点为C，求△OCB的面积．

21．先化简，再求值：(－4)÷ ，其中x＝－1

20． 已知：如图，在Rt△ABC中，∠C＝90°，AC＝．点D为BC边上一点，且BD＝2AD，∠ADC＝60°求△ABC的周长(结果保留根号)