
12、经、史、子、集是我国古代常有的图书分类。“经”主要指儒家经典,“史”是各种体裁的历史著作,“子”主要指诸子百家的著作及其他书籍,“集”指历代作家诗歌文词等。据此分类,《农政全书》应属于
A. 经部 B. 史部 C. 子部 D. 集部
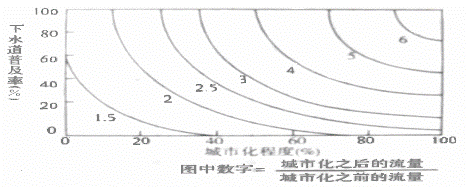 城市化进程大幅度改变了原有的水文生态。专家在进行城市化、下水道普及率以及径流量的相关分析研究时,将三者之间关系归纳如图。读图回答10-11题
城市化进程大幅度改变了原有的水文生态。专家在进行城市化、下水道普及率以及径流量的相关分析研究时,将三者之间关系归纳如图。读图回答10-11题
10.该图反映了
A.城市下水道普及率越高,产生径流越少 B.城市化水平越高,产生径流越少
 . 与城市相比,农村产生径流少
D.城市化水平越高,对水体污染越严重
. 与城市相比,农村产生径流少
D.城市化水平越高,对水体污染越严重
11.依据该模式推断,某地区1970年时城市化程度20℅,下水道普及率40℅;2000年城市化程度90℅,下水道普及率80℅.若年降水量不变,则2000年产生的径流量相当于1970年的
A.二分之一 B.三分之一 C.两倍 D.三倍
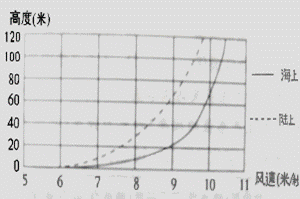 作为一种洁净能源,风能的开发越来越受到人们的关注。读陆地与海上风速剖面比较图回答7-9题
作为一种洁净能源,风能的开发越来越受到人们的关注。读陆地与海上风速剖面比较图回答7-9题
7.相同高度的风塔其发电能力
A.海上高于陆地
B. 陆地高于海上
 . 海上陆上相同
. 海上陆上相同
D. 无法判定
8.随着高度的增加,风速
A.陆地向上增速快 B. 海洋向上增速快
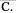 . 40米高度以内海上增速快 D.
40米高度以上陆上增速快
. 40米高度以内海上增速快 D.
40米高度以上陆上增速快
9.关于海上和陆上风速的叙述正确的是
A.风速差距由地面向高空增大 B.风速差距由海面向高空增大
 . 近地面增速小是地物阻力造成的 D.海上增速小是海浪阻力造成的
. 近地面增速小是地物阻力造成的 D.海上增速小是海浪阻力造成的
读“地质剖面及水循环”示意图完成5-6题
5.关于M的叙述正确的是
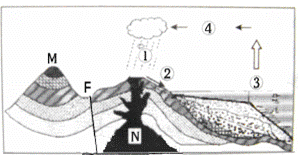 ①背斜山 ②向斜山 ③内力地貌 ④外力地貌
①背斜山 ②向斜山 ③内力地貌 ④外力地貌
A.①③ B. ②③
 . ②④
D.①④
. ②④
D.①④
6.关于图示地区地质作用的叙述正确的是
A.N为变质作用 B.N发生在F之后
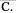 . M的形成于②无关 D.图示地区地质作用目前以内力作用为主
. M的形成于②无关 D.图示地区地质作用目前以内力作用为主
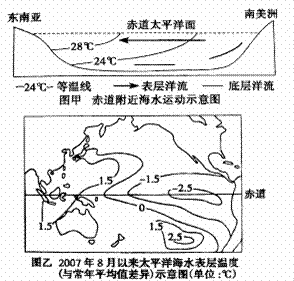 拉尼娜现象是指赤道附近东太平洋表面海水大规模持续异常偏冷的现象,又称反尼尔尼诺现象,它是大气环流系统与洋流系统相互作用的结果,会导致气候异常,气象灾害加剧。据甲、乙两图判断1-4题
拉尼娜现象是指赤道附近东太平洋表面海水大规模持续异常偏冷的现象,又称反尼尔尼诺现象,它是大气环流系统与洋流系统相互作用的结果,会导致气候异常,气象灾害加剧。据甲、乙两图判断1-4题
1、从垂直方向上看,赤道太平洋地区的大气流动应为
A. 东部气流上升B. 西部气流下沉
C. 呈顺时针流动D. 呈逆时针流动
2、乙图为2007年8月以来太平洋海水表层温度与常年平均值差异,图中反映出
A. 赤道东、西太平洋海水温度相差4度
B. 澳大利亚东、西岸水温相差1.5度
C. 东南太平洋为一暖水区,水温高于西太平洋
D. 西北太平洋中低纬度水温增幅较大
3、拉尼娜现象出现时,下列说法可信的是
A.秘鲁渔场捕鱼量减少 B.智利北部降水量增多
 . 印度尼西亚降水量增多 D.智利发生8.8级大地震
. 印度尼西亚降水量增多 D.智利发生8.8级大地震
4、拉尼娜现象的出现与洋流变化相关,下列说法可信的是
A赤道暖流增强 C北太平洋暖流减弱 B西风漂流减弱 D秘鲁上升流消失
(17)(本小题满分10分)
向量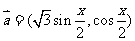 ,
,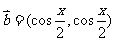 ,记
,记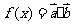 ,当
,当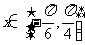 时, 试求
时, 试求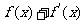 的值域.
的值域.
(18) (本小题满分12分)
已知袋中装有大小、形状完全相同的m个红球和n个白球,其中m、n满足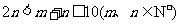 ,若从中任取2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
,若从中任取2个球,取出的2个球是同色的概率等于取出的2个球是异色的概率.
(Ⅰ) 求m、n的值;
(Ⅱ) 当m>4时,从袋中任取3个球,设取到红球的个数为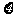 ,求
,求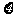 的分布列及数学期望.
的分布列及数学期望.
(19) (本小题满分12分)
|
|
|
|



 如图,侧棱垂直底面的三棱柱
如图,侧棱垂直底面的三棱柱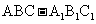 的底面ABC位于平行四边形ACDE中,AE=2,
的底面ABC位于平行四边形ACDE中,AE=2,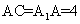 ,
,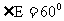 ,点B为DE中点.
B1
,点B为DE中点.
B1
|
|
|



 (Ⅰ) 求证:平面
(Ⅰ) 求证:平面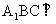 平面
平面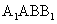 ;
;
(Ⅱ) 设二面角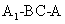 的大小为
的大小为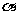 ,直线AC与平面
,直线AC与平面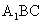 所成的角为
所成的角为 ,求
,求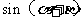 的值.
的值.
(20) (本小题满分12分)
已知数列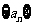 满足
满足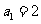 ,
,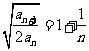 ;
;
(Ⅰ)求数列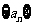 的通项公式;
的通项公式;
(Ⅱ)若数列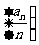 的前n项和为
的前n项和为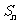 .,试比较
.,试比较 与2的大小.
与2的大小.
(21) (本小题满分12分)
已知椭圆C: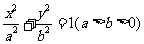 的离心率为
的离心率为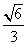 ,过右焦点F且斜率为1的直线交椭圆C于A、B两点,N为弦AB的中点.
,过右焦点F且斜率为1的直线交椭圆C于A、B两点,N为弦AB的中点.
(Ⅰ)求直线ON(O为坐标原点)的斜率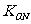 ;
;
(Ⅱ)对于椭圆C上任意一点M,试证:总存在角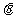
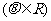 使等式:
使等式: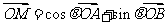 成立.
成立.
(22) (本小题满分12分)
已知函数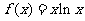 .
.
(Ⅰ)求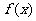 的最小值;
的最小值;
(Ⅱ)讨论关于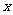 的方程
的方程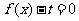 (
(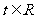 )的解的个数;
)的解的个数;
(Ⅲ)当m > o , n > o时,求证: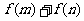 ≥
≥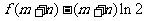 .
.
(13)已知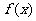 是R上的奇函数,且
是R上的奇函数,且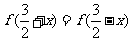 ,当
,当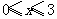 时,
时,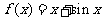 ,则
,则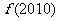 =
.
=
.
(14)已知b为二项式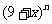 展开式中各项系数的和,且
展开式中各项系数的和,且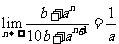 ;则实数a的取值范围是 .
;则实数a的取值范围是 .
(15)在三棱锥A-BCD中,P、Q分别是棱AC、BD上的点,连结AQ、CQ、BP、DP、PQ,若三棱锥A-BPQ、B-CPQ、C-DPQ的体积分别为6、2、8,则三棱锥A-BCD的体积为 .
(16)已知方程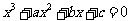 的三个实数根可分别作为一个椭圆、一双曲线、一抛物线的离心率,那么
的三个实数根可分别作为一个椭圆、一双曲线、一抛物线的离心率,那么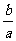 的取值范围是
.
的取值范围是
.
(1)若集合A={1,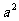 },B={2,4},则“
},B={2,4},则“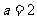 ”是“
”是“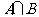 ={4}”的
={4}”的
A. 充分不必要条件 B. 必要不充分条件
 充分且必要条件
D. 既不充分也不必要条件
充分且必要条件
D. 既不充分也不必要条件
(2)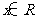 ,复数
,复数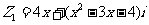 ,
,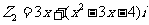 ,若
,若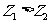 则
则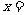
A. 0
B. 1 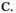 -1 D. 4
-1 D. 4
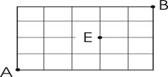 (3)如图,棋盘式街道,想从A经E到达B,若限制行进的方向只能向右或向上,则不同的走法共有
(3)如图,棋盘式街道,想从A经E到达B,若限制行进的方向只能向右或向上,则不同的走法共有
A. 126 种 B. 100种
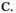 60 种
D. 20种
60 种
D. 20种
(4)满足条件: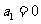 ,
,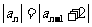 (
(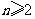 且
且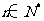 )的数列中,
)的数列中,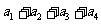 的最小值等于
的最小值等于
A. -4 B.
-6 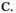 0 D. 2
0 D. 2
(5)如果直线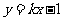 与椭圆
与椭圆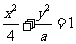 相切,那么
相切,那么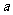 与
与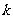 的取值范围是
的取值范围是
A. (0,1),(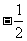 ,
,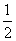 )
B.
)
B. 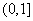 ,(
,(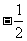 ,
,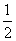 )
)
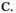 (0,1),
(0,1),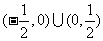 D.
D. 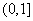 ,
,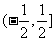
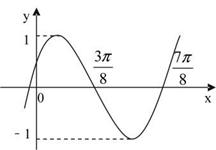 (6)已知函数
(6)已知函数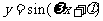 ,
,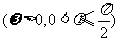 ,且此函数的图象如图所示,则点P
,且此函数的图象如图所示,则点P 的坐标为
的坐标为
(A. 2,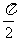 ) B. (2,
) B. (2, )
)
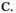 (4,
(4,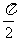 ) D. (4,
) D. (4, )
)
(7)异面直线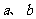 成
成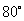 角,点
角,点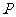 是
是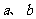 外的一定点,若过点
外的一定点,若过点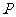 有且仅有2条直线与
有且仅有2条直线与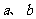 所成的角相等且等于
所成的角相等且等于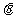 ,则
,则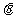 属于集合
属于集合
A. 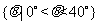 B.
B.
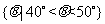
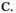
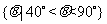 D.
D. 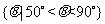
(8)已知曲线C: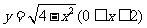 与函数
与函数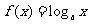 及函数
及函数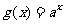 ,(其中
,(其中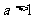 )的图像分别交于
)的图像分别交于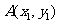 、
、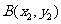 ,则
,则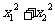 的值为
的值为
A. 16 B. 8 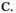 4 D. 2
4 D. 2
(9)设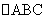 的三个内角A、B、C所对的三边分别为
的三个内角A、B、C所对的三边分别为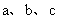 ,若
,若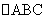 的面积
的面积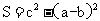 ,则
,则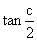 =
=
A. 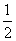 B.
B. 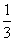
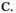
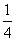 D.
D.
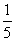
(10)对任意的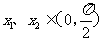 ,
,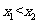 ,
,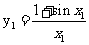 ,
,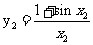 ;则
;则
A.  B.
B.
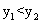
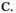
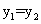 D.
无法确定
D.
无法确定
(11)已知点O是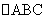 内一点,且满足
内一点,且满足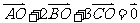 ,设Q是CO的延长线与AB的交点,记
,设Q是CO的延长线与AB的交点,记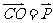 ,则
,则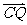 =
=
A. 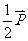 B.
B.
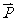
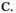
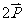 D.
D.
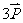
(12)抛物线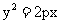
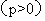 的焦点为F,点A、B在抛物线上,且
的焦点为F,点A、B在抛物线上,且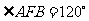 ,弦AB中点M在准线l上的射影为
,弦AB中点M在准线l上的射影为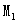 ,则
,则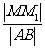 的最大值为
的最大值为
A. 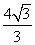 B.
B. 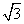
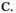
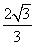 D.
D. 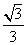
第II卷(非选择题 共90分)
20. (本小题满分12分)
(本小题满分12分)
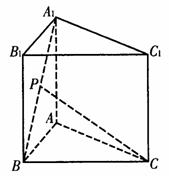
已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为
A1B上的点,且PC⊥AB.
(Ⅰ)求二面角P-AC-B的正切值;
(Ⅱ)求点B到平面PAC的距离.
21 (本小题满分12分)
已知定义在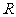 上的函数
上的函数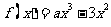 (
(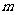 为常数)。
为常数)。
(1)
若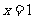 是函数
是函数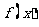 的一个极值点,求实数
的一个极值点,求实数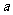 的值;
的值;
(2)
若函数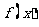 在
在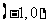 上是增函数,求实数
上是增函数,求实数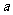 的取值范围;
的取值范围;
(3)
若函数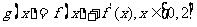 在
在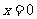 处取得最大值,求正数
处取得最大值,求正数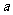 的取值 范围。
的取值 范围。
22(本小题满分12分)
已知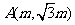 和
和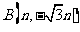
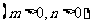 两点分别在射线
两点分别在射线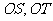 上移动,且
上移动,且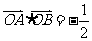 (
(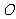 为坐标原点),动点
为坐标原点),动点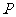 满足
满足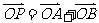
(1)
求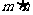 的值
的值
(2)
求点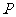 的轨迹
的轨迹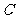 的方程,并说明它表示怎样的曲线?
的方程,并说明它表示怎样的曲线?
(3)
若直线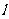 过点
过点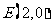 交(2)中曲线
交(2)中曲线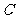 于
于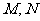 两点,且
两点,且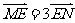 ,求
,求 的方程.
的方程.
19. (本小题满分12分)
甲、乙两支中学生足球队,苦战90分钟,比分2:2,现决定各派5名队员,每人射一个点球决定胜负,假设两支球队派出的队员点球命中概率均为0.5。
(1)两队球员一个间隔一个出场射球,有多少种不同的出场顺序?
(2)不考虑乙球队,甲球队五名队员有连续两个队员射中,且其余队员均未射中,概率是多少?
(3)甲乙两队各射完5个点球后,再次出现平局的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com