
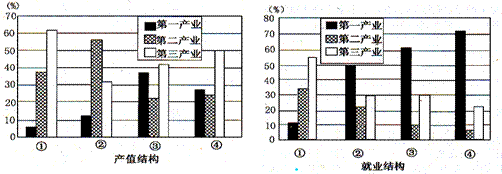
2. 产值结构与就业结构比较一致的地区是
产值结构与就业结构比较一致的地区是
A.① B.②
C.③ D.④
右图为某地交通线路示意图。据此回答3-4题。
1.从去年开始国家鼓励汽车、家电“以旧换新”。鼓励汽车、家电“以旧换新”政策实施后,可更新老旧汽车100万辆、家电500万台,直接拉动市场消费1000-1200亿元;回收利用各种资源近230万吨;稳定和扩大就业近5万人。报废汽车、废旧家电回收拆解行业属于
A.劳动力密集型 B.技术密集型 C.资源密集型 D.能源密集型
下图表示近年我国四个地区三大产业的产值结构和就业结构。读图回答2题。
21. 解:(1)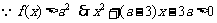
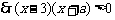 对
对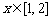 恒成立,
恒成立,
又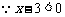 恒成立,
恒成立, 对
对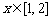 恒成立,
恒成立,
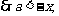 又
又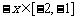 ,
,
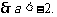 ………………4分
………………4分
(2)由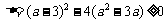 得:
得: ,
,
不妨设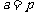 ,则q,r恰为方程两根,由韦达定理得:
,则q,r恰为方程两根,由韦达定理得:
①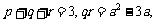
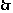 ②
②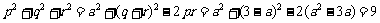
③而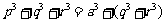
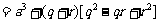
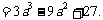 ……7分
……7分
设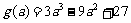 ,求导得:
,求导得: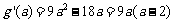
当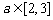 时,
时,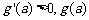 递增;当
递增;当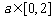 时,
时,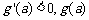 递减;
递减;
当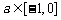 时,
时,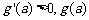 递增,
递增,
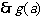 在
在 上的最小值为
上的最小值为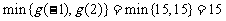 ……………10分
……………10分
(3)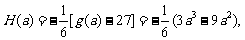
如果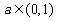 ,则
,则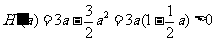
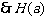 在
在 为递增函数,
为递增函数,
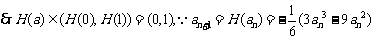
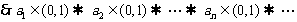
又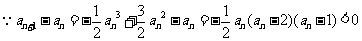
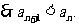 …………………………………14分
…………………………………14分
20. 解:(Ⅰ)由数阵的排布规律可知:
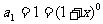 ,
,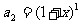 ,
, ,
,
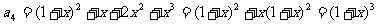 ,…
,…
猜想: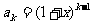
 .
(3分)
.
(3分)
(Ⅱ)由数阵的排布规律可知:
第1行: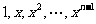
第2行:
第3行:
… …
因为 ;所以数阵中除第
;所以数阵中除第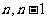 行外,其余各行均为等比数列,
行外,其余各行均为等比数列,
且公比为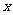 ,又第
,又第 行的首项为
行的首项为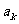 ,项数为
,项数为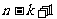 ,
,
∴当 时
时
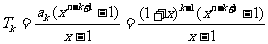 ①
①
当 时,第
时,第 行为常数列,
行为常数列,
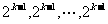 (共有
(共有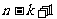 行)
行)
∴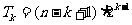 ②
②
又当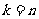 时,
时,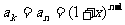
当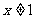 时,①式为
时,①式为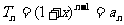
当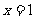 时,②式为
时,②式为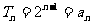
当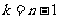 时,由排布规律可知,第
时,由排布规律可知,第 行两个数之和为
行两个数之和为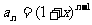
而在①式中,即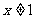 时,
时,
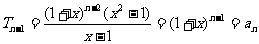
在②式中,即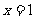 时
时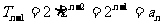
即当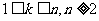 时,都有
时,都有
 (9分)
(9分)
(Ⅲ)当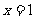 时,
时,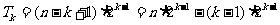
∴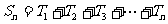
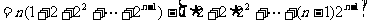 ,
,
在上式中,前面一部分直接用等比数列求和公式求得和为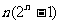 ,
,
后一部分可用错位相减法求得和为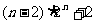 ;
;
∴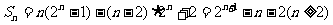 .
(13分)
.
(13分)
19. 解:(1)输出4包括2个互斥事件,分别是:以2为自变量,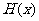 是
是 ,以1为自变量,
,以1为自变量,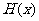 是
是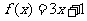 ,
,
故所求概率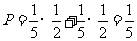 ;……… 6分
;……… 6分
(2)将程序运行一次,输出的结果是奇数包括1,7,9,13,25这5种情况,
故运行一次输出奇数的概率是 ,………10分
,………10分
由独立重复试验的概率计算公式得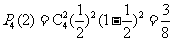 …………12分
…………12分
17. 解:解法一:(Ⅰ)存在且为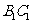 的中点,连接
的中点,连接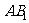 ,
,
∵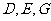 分别是
分别是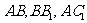 的中点, ∴
的中点, ∴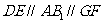 .
.
 (Ⅱ)延长
(Ⅱ)延长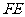 与
与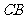 的延长线交于
的延长线交于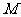 ,连接
,连接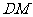 ,
,
则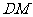 为截面与底面所成二面角的棱,
为截面与底面所成二面角的棱,
取 的中点
的中点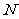 ,连
,连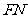 ,则
,则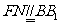 .
.
∵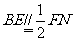 ,∴
,∴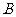 为
为 的中点.
的中点.
由题设得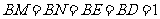 ,且
,且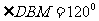 ,
,
作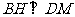 于
于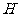 ,则
,则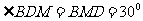 ,连
,连 ,
,
又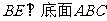 ,
,
由三垂线定理可知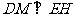 ,
,
∴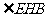 为截面与底面所成的锐二面角.
为截面与底面所成的锐二面角.
在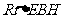 中,
中,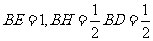 ,
,
∴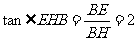 .
.
解法二:(Ⅱ)如图,以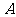 为坐标原点,
为坐标原点,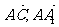 的方向分别作为
的方向分别作为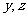 轴的正方向建立空间直
轴的正方向建立空间直
角坐标系,则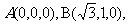
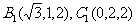 ;∵
;∵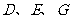 分别是
分别是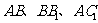
的中点,∴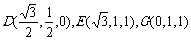 ,
,
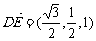 ,
,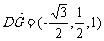 ;
;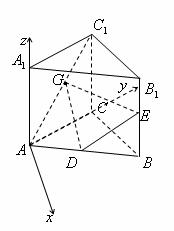
设平面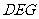 的法向量为
的法向量为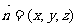 ,
,
由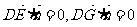
得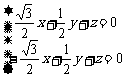 ,解得
,解得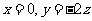 ,
,
取 得
得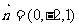 ;
;
又平面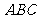 的一个法向量为
的一个法向量为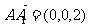 ,
(6分)
,
(6分)
设截面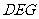 与底面
与底面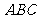 所成锐二面角为
所成锐二面角为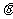
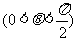 ,
,
则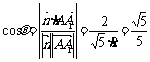 ,
,
∴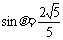 ,得
,得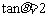 .
.
故截面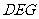 与底面
与底面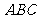 所成锐二面角的正切值为2.
所成锐二面角的正切值为2.
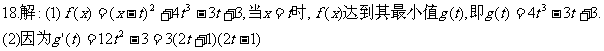
|
t |
 |
 |
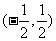 |
 |
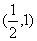 |
|
g'(t) |
+ |
0 |
- |
0 |
+ |
|
g(t) |
↗ |
极大值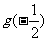 |
↙ |
极小值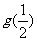 |
↗ |
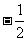
由此可见,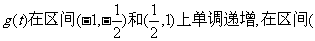
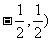 上单调递减.…8分
上单调递减.…8分

综合可得k的取值范围为:k≥4.
21.已知函数 (a为常数)
(1)如果对任意
(a为常数)
(1)如果对任意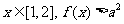 恒成立,求实数a的取值范围;
(2)设实数
恒成立,求实数a的取值范围;
(2)设实数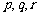 满足:
满足: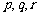 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程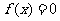 的两实根,判断①
的两实根,判断①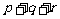 ,②
,②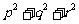 ,③
,③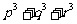 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数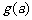 ,并求
,并求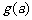 的最小值;
(3)对于(2)中的
的最小值;
(3)对于(2)中的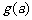 ,设
,设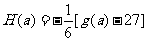 ,数列
,数列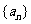 满足
满足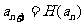
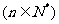 ,且
,且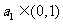 ,试判断
,试判断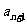 与
与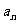 的大小,并证明。
的大小,并证明。
襄樊五中文科数学测试题
BBACD CCACC 85 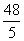
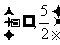
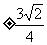

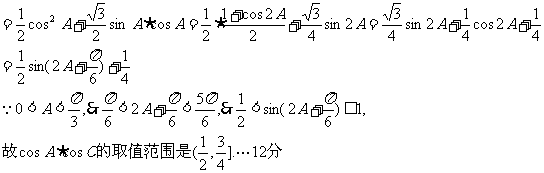
20.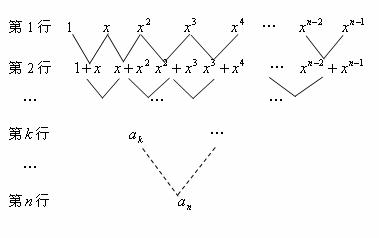 下图是一个三角形数阵
下图是一个三角形数阵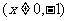 ,从第二行起每个数都等于它肩上两个数的和,第
,从第二行起每个数都等于它肩上两个数的和,第 行的第一个数为
行的第一个数为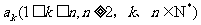 (Ⅰ)写出
(Ⅰ)写出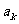 关于
关于 的表达式:
的表达式:
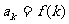 ,不需证明。
(Ⅱ)求第
,不需证明。
(Ⅱ)求第 行中所有数的和
行中所有数的和 ;
(Ⅲ)当
;
(Ⅲ)当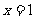 时,求数阵中所有
数的和
时,求数阵中所有
数的和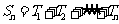 .
.
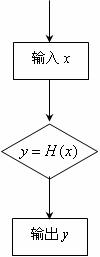
19.右图的程序可产生一系列随机数,其工作原理如下:
①从集合D中随机抽取1个数作为自变量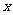 输入;
②从函数
输入;
②从函数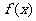 与
与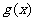 中随机选择一个作为
中随机选择一个作为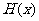 进行计算;
③输出函数值
进行计算;
③输出函数值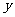 。
若
。
若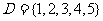 ,
,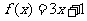 ,
, ,
(1)求
,
(1)求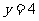 的概率;
(2)将程序运行4次,求恰好有2次的输出结果是奇数的概率
的概率;
(2)将程序运行4次,求恰好有2次的输出结果是奇数的概率
18. 设函数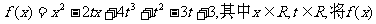 的最小值记为g(t).
(1)求g(t)的表达式;
(2)讨论g(t)在区间[-1,1]内的单调性;
(3)当
的最小值记为g(t).
(1)求g(t)的表达式;
(2)讨论g(t)在区间[-1,1]内的单调性;
(3)当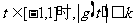 恒成立,其中k为正数,求k的取值范围.
恒成立,其中k为正数,求k的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com