
8.(上海理综)如图是位于锦江乐园的摩天轮,高度为108m,直径是98m。一质量为50kg的游客乘坐该摩天轮做匀速圆周运动旋转一圈需25min。如果以地面为零势能面,则他到达最高处时的(取g=10m/s2)( )。

A.重力势能为5.4×104J,角速度为0.2rad/s
B.重力势能为4.9×104J,角速度为0.2rad/s
C.重力势能为5.4×104J,角速度为4.2×10-3rad/s
D.重力势能为4.9×104J,角速度为4.2×10-3rad/s
答案:C
16.(北京卷)一物体静置在平均密度为 的球形天体表面的赤道上。已知万有引力常量G,若由于天体自转使物体对天体表面压力恰好为零,则天体自转周期为
的球形天体表面的赤道上。已知万有引力常量G,若由于天体自转使物体对天体表面压力恰好为零,则天体自转周期为
A.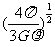 B.
B. C.
C.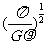 D.
D.
答案:D
[解析]赤道表面的物体对天体表面的压力为零,说明天体对物体的万有引力恰好等于物体随天体转动所需要的向心力,有 ,化简得
,化简得 ,正确答案为D。
,正确答案为D。
20.(新课标卷)太阳系中的8大行星的轨道均可以近似看成圆轨道.下列4幅图是用来描述这些行星运动所遵从的某一规律的图像.图中坐标系的横轴是 ,纵轴是
,纵轴是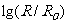 ;这里T和R分别是行星绕太阳运行的周期和相应的圆轨道半径,
;这里T和R分别是行星绕太阳运行的周期和相应的圆轨道半径, 和
和 分别是水星绕太阳运行的周期和相应的圆轨道半径.下列4幅图中正确的是
分别是水星绕太阳运行的周期和相应的圆轨道半径.下列4幅图中正确的是

答案:B
解析:根据开普勒周期定律:周期平方与轨道半径三次方正比可知 ,
,
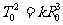 两式相除后取对数,得:
两式相除后取对数,得: ,整理得:
,整理得: ,选项B正确。
,选项B正确。
21.(全国卷2)已知地球同步卫星离地面的高度约为地球半径的6倍。若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,则该行星的自转周期约为
A.6小时 B. 12小时 C. 24小时 D. 36小时
[答案]B
[解析]地球的同步卫星的周期为T1=24小时,轨道半径为r1=7R1,密度ρ1。某行星的同步卫星周期为T2,轨道半径为r2=3.5R2,密度ρ2。根据牛顿第二定律和万有引力定律分别有


两式化简得 小时
小时
[命题意图与考点定位]牛顿第二定律和万有引力定律应用于天体运动。
25.(全国卷1)(18分)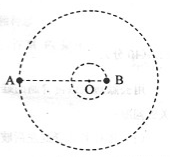 如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。
如右图,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。
⑴ 求两星球做圆周运动的周期。
⑵ 在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg 和 7.35 ×1022kg 。求T2与T1两者平方之比。(结果保留3位小数)
[答案]⑴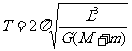 ⑵1.01
⑵1.01
[解析] ⑴A和B绕O做匀速圆周运动,它们之间的万有引力提供向心力,则A和B的向心力相等。且A和B和O始终共线,说明A和B有相同的角速度和周期。因此有
 ,
, ,连立解得
,连立解得 ,
,
对A根据牛顿第二定律和万有引力定律得
化简得 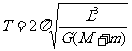
⑵将地月看成双星,由⑴得
将月球看作绕地心做圆周运动,根据牛顿第二定律和万有引力定律得
化简得 
所以两种周期的平方比值为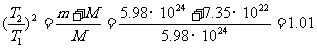
22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分。
若实数 、
、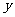 、
、 满足
满足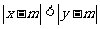 ,则称
,则称 比
比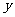 接近
接近 .
.
(1)若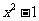 比3接近0,求
比3接近0,求 的取值范围;
的取值范围;
(2)对任意两个不相等的正数 、
、 ,证明:
,证明: 比
比 接近
接近 ;
;
(3)已知函数 的定义域
的定义域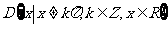 .任取
.任取 ,
, 等于
等于 和
和 中接近0的那个值.写出函数
中接近0的那个值.写出函数 的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明).
23(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知椭圆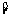 的方程为
的方程为 ,
, 、
、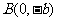 和
和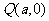 为
为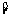 的三个顶点.
的三个顶点.
(1)若点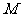 满足
满足 ,求点
,求点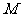 的坐标;
的坐标;
(2)设直线 交椭圆
交椭圆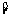 于
于 、
、 两点,交直线
两点,交直线 于点
于点 .若
.若 ,证明:
,证明: 为
为 的中点;
的中点;
(3)设点 在椭圆
在椭圆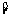 内且不在
内且不在 轴上,如何构作过
轴上,如何构作过 中点
中点 的直线
的直线 ,使得
,使得 与椭圆
与椭圆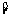 的两个交点
的两个交点 、
、 满足
满足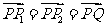 ?令
?令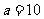 ,
, ,点
,点 的坐标是(-8,-1),若椭圆
的坐标是(-8,-1),若椭圆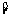 上的点
上的点 、
、 满足
满足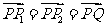 ,求点
,求点 、
、 的坐标.
的坐标.
21.(本题满分14分)本题共有2个小题,第一个小题满分6分,第2个小题满分8分。
已知数列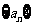 的前
的前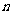 项和为
项和为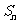 ,且
,且 ,
,
(1)证明: 是等比数列;
是等比数列;
(2)求数列 的通项公式,并求出使得
的通项公式,并求出使得 成立的最小正整数
成立的最小正整数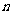 .
.
20.(本大题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
 如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用
如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,再用 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
平方米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径 取何值时,
取何值时, 取得最大值?并求出该
取得最大值?并求出该
最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出
用于灯笼的三视图(作图时,不需考虑骨架等因素).
19.(本题满分12分)
已知 ,化简:
,化简:
 .
.
18.若△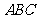 的三个内角满足
的三个内角满足 ,则△
,则△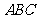
(A)一定是锐角三角形. (B)一定是直角三角形.
(C)一定是钝角三角形. (D)可能是锐角三角形,也可能是钝角三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com