
3.下列四种现象中,可以用右图表示的是
A.在适宜条件下光合作用强度随CO2含量的变化
B.条件适宜、底物充足时反应速率随酶量的变化
C.一个细胞周期中DNA含量随时间的变化
D.理想条件下种群数量随时间的变化
[解析]本题主要考查相关生理过程中的数量变化趋势,涉及到新陈代谢与细胞分裂的相关内容,考查学生的理解能力和获取信息的能力。如图曲线的走势为先增加后稳定,曲线有两个关键点:即起点(m,0)(m>0)和饱和点。符合这一曲线的为A选项;B项对应的曲线起点不正确,曲线的走势一直为增函数,不会出现饱和效应;C项对应的曲线就更不正确了,起点纵坐标等于终点,且大于0;D项曲线为种群的“J”型增长曲线。
[答案]A
2.光照条件下,给C3植物和C4 植物叶片提供14CO2,然后检测叶片中的14C。下列有关检测结果的叙述,错误的是
A.从C3植物的淀粉和C4植物的葡萄糖中可检测到14C
B.在C3植物和C4植物呼吸过程产生的中间产物中可检测到14C
C.随光照强度增加,从C4植物叶片中可检测到含14C的C4大量积累
D.在C3植物叶肉组织和C4植物维管束鞘的C3中可检测到14C
 [解析]本题主要考查C3植物和C4 植物的光合作用及同位素标记法,考查学生的理解能力、实验与探究能力和综合运用能力。根据C3植物和C4 植物光合作用暗反应的场所、过程[C3植物:C5+14CO2→2C3(只有两个14C)→C5+(14CH2O);和C4植C4植物的光合作用:C3+14CO2→C4(只有一个14C)→C3+14CO2,C5+14CO2→2C3(只有两个14C)→C5+(14CH2O)]和呼吸作用的过程[C6H12O6+6O2+6H2O→6H2O+12CO2]可知,A、B和D三项均正确;C4途径中的C4为中间代谢产物,不可能大量的积累。
[解析]本题主要考查C3植物和C4 植物的光合作用及同位素标记法,考查学生的理解能力、实验与探究能力和综合运用能力。根据C3植物和C4 植物光合作用暗反应的场所、过程[C3植物:C5+14CO2→2C3(只有两个14C)→C5+(14CH2O);和C4植C4植物的光合作用:C3+14CO2→C4(只有一个14C)→C3+14CO2,C5+14CO2→2C3(只有两个14C)→C5+(14CH2O)]和呼吸作用的过程[C6H12O6+6O2+6H2O→6H2O+12CO2]可知,A、B和D三项均正确;C4途径中的C4为中间代谢产物,不可能大量的积累。
[答案]C
1. 下列过程中,不直接依赖细胞膜的流动性就能完成的是
A.植物体胞杂交中原生质体融合 B.mRNA与游离核糖体的结合
C.胰岛B细胞分泌胰岛素 D.吞噬细胞对抗原的摄取
[解析]本题主要考查细胞膜的结构特点-具有一定的流动性,考查学生的理解能力。植物体细胞杂交中原生质体的融合依赖于细胞膜的流动性,胰岛B细胞分泌胰岛素的过程属于外排作用,吞噬细胞对抗原的摄取属于内吞作用,内吞和外排作用均与细胞膜的流动性有直接的关系;而mRNA与游离核糖体的结合与细胞膜的流动性无关。
[答案]B
(17)(本小题满分12分)
已知函数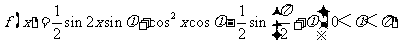 ,其图象过点(
,其图象过点(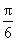 ,
,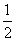 ).
).
(Ⅰ)求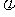 的值;
的值;
(Ⅱ)将函数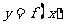 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的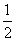 ,纵坐标不变,得到函数
,纵坐标不变,得到函数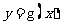 的图象,求函数
的图象,求函数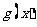 在[0,
在[0, 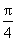 ]上的最大值和最小值.
]上的最大值和最小值.
[解析](Ⅰ)因为已知函数图象过点(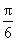 ,
,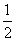 ),所以有
),所以有
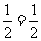
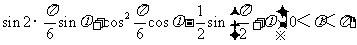 ,即有
,即有
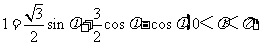 =
=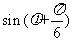 ,所以
,所以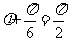 ,解得
,解得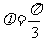 。
。
(Ⅱ)由(Ⅰ)知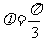 ,所以
,所以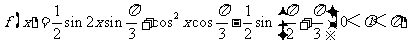
=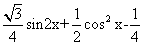 =
=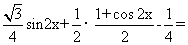
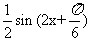 ,
,
所以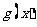 =
= ,因为x
,因为x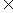 [0,
[0, 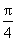 ],所以
],所以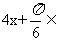
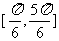 ,
,
所以当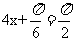 时,
时,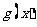 取最大值
取最大值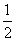 ;当
;当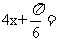
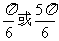 时,
时,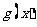 取最小值
取最小值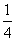 。
。
[命题意图]本题考查三角函数的诱导公式及二倍角等基本公式的灵活应用、图象变换以及三角函数的最值问题、分析问题与解决问题的能力。
(18)(本小题满分12分)
已知等差数列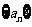 满足:
满足: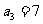 ,
,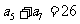 ,
,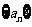 的前n项和为
的前n项和为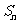 .
.
(Ⅰ)求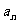 及
及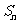 ;
;
(Ⅱ)令bn=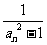 (n
(n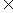 N*),求数列
N*),求数列 的前n项和
的前n项和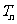 .
.
[解析](Ⅰ)设等差数列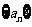 的公差为d,因为
的公差为d,因为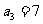 ,
,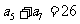 ,所以有
,所以有
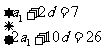 ,解得
,解得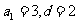 ,
,
所以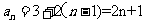 ;
;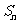 =
=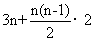 =
= 。
。
(Ⅱ)由(Ⅰ)知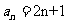 ,所以bn=
,所以bn=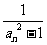 =
=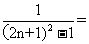
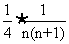 =
=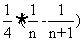 ,
,
所以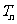 =
=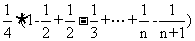 =
=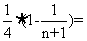
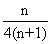 ,
,
即数列 的前n项和
的前n项和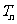 =
=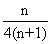 。
。
[命题意图]本题考查等差数列的通项公式与前n项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键。
 (19)(本小题满分12分)
(19)(本小题满分12分)
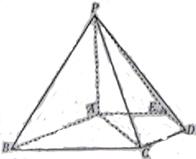
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,  ABC=45°,AB=2
ABC=45°,AB=2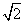 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P-ACDE的体积.
[解析](Ⅰ)证明:因为 ABC=45°,AB=2
ABC=45°,AB=2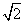 ,BC=4,所以在
,BC=4,所以在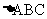 中,由余弦定理得:
中,由余弦定理得: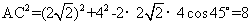 ,解得
,解得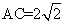 ,
,
所以 ,即
,即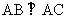 ,又PA⊥平面ABCDE,所以PA⊥
,又PA⊥平面ABCDE,所以PA⊥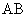 ,
,
又PA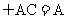 ,所以
,所以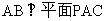 ,又AB∥CD,所以
,又AB∥CD,所以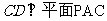 ,又因为
,又因为
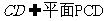 ,所以平面PCD⊥平面PAC;
,所以平面PCD⊥平面PAC;
(Ⅱ)由(Ⅰ)知平面PCD⊥平面PAC,所以在平面PAC内,过点A作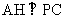 于H,则
于H,则
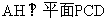 ,又AB∥CD,AB
,又AB∥CD,AB 平面
平面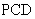 内,所以AB平行于平面
内,所以AB平行于平面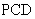 ,所以点A到平面
,所以点A到平面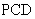 的距离等于点B到平面
的距离等于点B到平面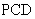 的距离,过点B作BO⊥平面
的距离,过点B作BO⊥平面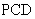 于点O,则
于点O,则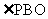 为所求角,且
为所求角,且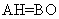 ,又容易求得
,又容易求得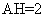 ,所以
,所以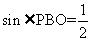 ,即
,即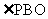 =
=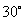 ,所以直线PB与平面PCD所成角的大小为
,所以直线PB与平面PCD所成角的大小为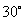 ;
;
(Ⅲ)由(Ⅰ)知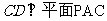 ,所以
,所以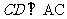 ,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得
,又AC∥ED,所以四边形ACDE是直角梯形,又容易求得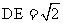 ,AC=
,AC=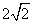 ,所以四边形ACDE的面积为
,所以四边形ACDE的面积为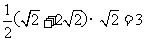 ,所以
,所以
四棱锥P-ACDE的体积为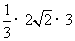 =
=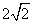 。
。
[命题意图]本题考查了空间几何体的的线面与面面垂直、线面角的求解以及几何体的体积计算问题,考查了同学们的空间想象能力以及空间思维能力。
(20)(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有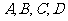 四个问题,规则如下:
四个问题,规则如下:
① 每位参加者计分器的初始分均为10分,答对问题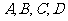 分别加1分、2分、3分、6分,答错任一题减2分;
分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,计分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局,当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题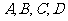 顺序作答,直至答题结束.
顺序作答,直至答题结束.
假设甲同学对问题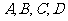 回答正确的概率依次为
回答正确的概率依次为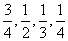 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用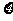 表示甲同学本轮答题结束时答题的个数,求
表示甲同学本轮答题结束时答题的个数,求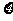 的分布列和数学的
的分布列和数学的 .
.
[解析](Ⅰ)因为甲同学能进入下一轮与淘汰出局互为对立事件,所以甲同学能进入下一轮的概率为1-(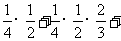
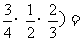
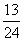 ;
;
(Ⅱ)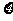 可能取2,3,4,则
可能取2,3,4,则

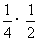 =
=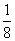 ;
;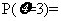
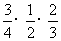 +
+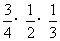 +
+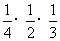 =
=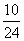 ;
;

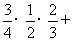
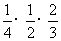
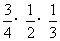 =
=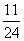 ,
,
所以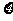 的分布列为
的分布列为
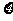 |
2 |
3 |
4 |
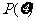 |
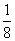 |
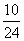 |
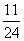 |
数学期望 =
=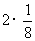 +
+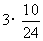 +4
+4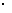
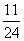 =
=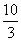 。
。
[命题意图]本题考查了相互独立事件同时发生的概率、考查了离散型随机变量的分布列以及数学期望的知识,考查了同学们利用所学知识解决实际问题的能力。
(21)(本小题满分12分)
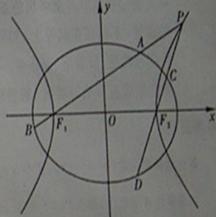
如图,已知椭圆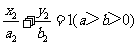 的离心率为
的离心率为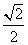 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点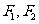 为顶点的三角形的周长为
为顶点的三角形的周长为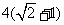 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设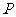 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线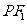 和
和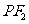 与椭圆的交点分别为
与椭圆的交点分别为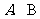 和
和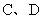 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线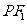 、
、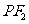 的斜率分别为
的斜率分别为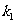 、
、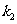 ,证明
,证明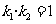 ;
;
(Ⅲ)是否存在常数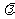 ,使得
,使得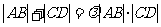 恒成立?若存在,求
恒成立?若存在,求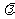 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
[解析](Ⅰ)由题意知,椭圆离心率为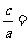
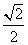 ,得
,得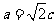 ,又
,又
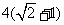 ,所以可解得
,所以可解得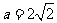 ,
,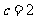 ,所以
,所以 ,所以椭圆的标准方程为
,所以椭圆的标准方程为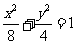 ;所以椭圆的焦点坐标为(
;所以椭圆的焦点坐标为( ,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,所以该双曲线的标准方程为
,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,所以该双曲线的标准方程为
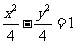 。
。
(Ⅱ)设点P( ,
,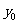 ),则
),则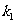 =
=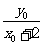 ,
,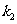 =
=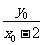 ,所以
,所以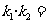
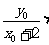
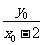 =
=
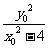 ,又点P(
,又点P( ,
,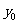 )在双曲线上,所以有
)在双曲线上,所以有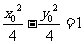 ,即
,即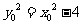 ,所以
,所以
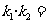
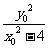 =1。
=1。
(Ⅲ)假设存在常数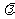 ,使得
,使得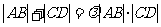 恒成立,则由(Ⅱ)知
恒成立,则由(Ⅱ)知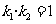 ,所以设直线AB的方程为
,所以设直线AB的方程为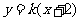 ,则直线CD的方程为
,则直线CD的方程为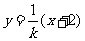 ,
,
由方程组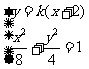 消y得:
消y得: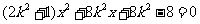 ,设
,设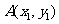 ,
,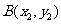 ,
,
则由韦达定理得: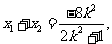
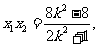
所以|AB|=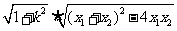 =
=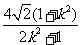 ,同理可得
,同理可得
|CD|=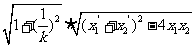 =
=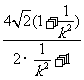 =
= ,
,
又因为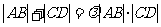 ,所以有
,所以有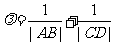 =
=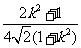 +
+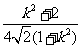
=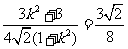 ,所以存在常数
,所以存在常数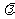
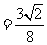 ,使得
,使得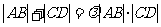 恒成立。
恒成立。
[命题意图]本题考查了椭圆的定义、离心率、椭圆与双曲线的标准方程、直线与圆锥曲线的位置关系,是一道综合性的试题,考查了学生综合运用知识解决问题的能力。其中问题(3)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力,
(22)(本小题满分14分)
已知函数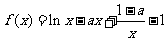
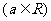 .
.
(Ⅰ)当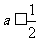 时,讨论
时,讨论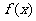 的单调性;
的单调性;
(Ⅱ)设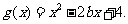 当
当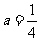 时,若对任意
时,若对任意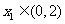 ,存在
,存在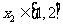 ,使
,使
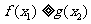 ,求实数
,求实数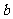 取值范围.
取值范围.
[解析](Ⅰ)原函数的定义域为(0,+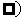 ,因为
,因为 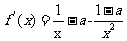 =
=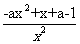 ,所以
,所以
当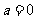 时,
时,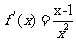 ,令
,令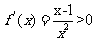 得
得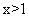 ,所以
,所以
此时函数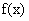 在(1,+
在(1,+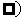 上是增函数;在(0,1)上是减函数;
上是增函数;在(0,1)上是减函数;
当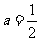 时,
时,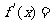
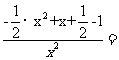
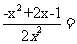
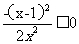 ,所以
,所以
此时函数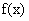 在(0,+
在(0,+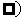 是减函数;
是减函数;
当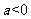 时,令
时,令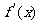 =
=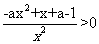 得
得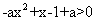 ,解得
,解得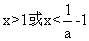 (舍去),此时函数
(舍去),此时函数
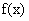 在(1,+
在(1,+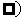 上是增函数;在(0,1)上是减函数;
上是增函数;在(0,1)上是减函数;
当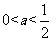 时,令
时,令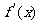 =
=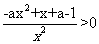 得
得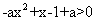 ,解得
,解得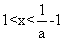 ,此时函数
,此时函数
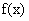 在(1,
在(1,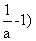 上是增函数;在(0,1)和
上是增函数;在(0,1)和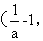 +
+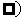 上是减函数;
上是减函数;
当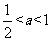 时,令
时,令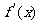 =
=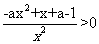 得
得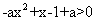 ,解得
,解得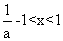 ,此时函数
,此时函数
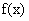 在
在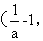 1)上是增函数;在(0,
1)上是增函数;在(0,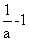 )和
)和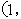 +
+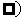 上是减函数;
上是减函数;
当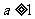 时,由于
时,由于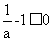 ,令
,令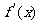 =
=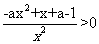 得
得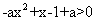 ,可解得0
,可解得0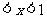 ,此时函数
,此时函数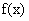 在(0,1)上是增函数;在(1,+
在(0,1)上是增函数;在(1,+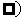 上是减函数。
上是减函数。
(Ⅱ)当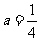 时,
时,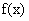 在(0,1)上是减函数,在(1,2)上是增函数,所以对任意
在(0,1)上是减函数,在(1,2)上是增函数,所以对任意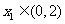 ,
,
有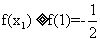 ,又已知存在
,又已知存在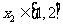 ,使
,使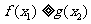 ,所以
,所以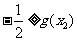 ,
,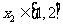 ,
,
即存在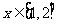 ,使
,使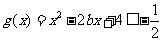 ,即
,即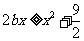 ,即
,即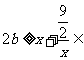
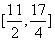 ,
,
所以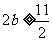 ,解得
,解得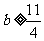 ,即实数
,即实数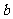 取值范围是
取值范围是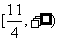 。
。
[命题意图]本题将导数、二次函数、不等式知识有机的结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力。
(1)直接利用函数与导数的关系讨论函数的单调性;(2)利用导数求出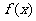 的最小值、利用二次函数知识或分离常数法求出
的最小值、利用二次函数知识或分离常数法求出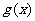 在闭区间[1,2]上的最大值,然后解不等式求参数。
在闭区间[1,2]上的最大值,然后解不等式求参数。
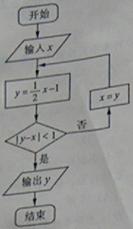 (13)执行右图所示的程序框图,若输入
(13)执行右图所示的程序框图,若输入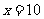 ,则输出
,则输出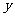 的值为
.
的值为
.
[答案]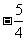
[解析]当x=10时,y=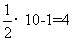 ,此时|y-x|=6;
,此时|y-x|=6;
当x=4时,y= ,此时|y-x|=3;当x=1时,y=
,此时|y-x|=3;当x=1时,y=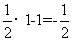 ,此时|y-x|=
,此时|y-x|=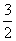 ;
;
当x= 时,y=
时,y=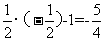 ,此时|y-x|=
,此时|y-x|=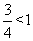 ,故输出y的值为
,故输出y的值为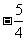 。
。
[命题意图]本题考查程序框图的基础知识,考查了同学们的试图能力。
(14)若对任意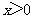 ,
,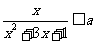 恒成立,则
恒成立,则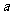 的取值范围是
.
的取值范围是
.
[答案]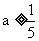
[解析]因为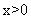 ,所以
,所以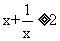 (当且仅当
(当且仅当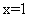 时取等号),所以有
时取等号),所以有
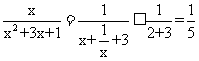 ,即
,即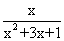 的最大值为
的最大值为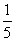 ,故
,故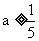 。
。
[命题意图]本题考查了分式不等式恒成立问题以及参数问题的求解,考查了同学们的转化能力。属中档题。
(15)在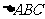 中,角
中,角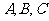 所对的边分别为a,b,c,若
所对的边分别为a,b,c,若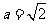 ,
,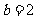 ,
,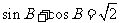 ,则角
,则角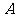 的大小为
.
的大小为
.
[答案]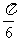
[解析]由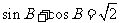 得
得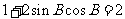 ,即
,即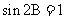 ,因为
,因为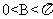 ,所以
,所以
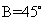 ,又因为
,又因为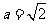 ,
,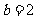 ,所以在
,所以在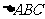 中,由正弦定理得:
中,由正弦定理得: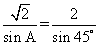 ,解得
,解得
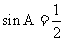 ,又
,又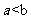 ,所以
,所以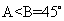 ,所以
,所以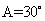 。
。
[命题意图]本题考查了三角恒等变换、已知三角函数值求解以及正弦定理,考查了同学们解决三角形问题的能力,属于中档题。
(16)已知圆C过点(1,0),且圆心在x轴的正半轴上,直线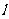 :
: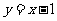 被圆C所截得的弦长为
被圆C所截得的弦长为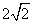 ,则过圆心且与直线
,则过圆心且与直线 垂直的直线的方程为
.
垂直的直线的方程为
.
[答案]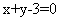
[解析]由题意,设所求的直线方程为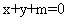 ,设圆心坐标为
,设圆心坐标为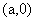 ,则由题意知:
,则由题意知:
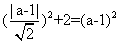 ,解得
,解得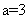 或-1,又因为圆心在x轴的正半轴上,所以
或-1,又因为圆心在x轴的正半轴上,所以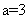 ,故圆心坐标为
,故圆心坐标为
(3,0),因为圆心(3,0)在所求的直线上,所以有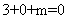 ,即
,即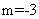 ,故所求的直线方程为
,故所求的直线方程为
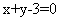 。
。
[命题意图]本题考查了直线的方程、点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
有一项是满足题目要求的.
(1)
已知全集U=R,集合M={x||x-1| 2},则
2},则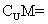
(A){x|-1<x<3} (B){x|-1 x
x 3} (C){x|x<-1或x>3}
(D){x|x
3} (C){x|x<-1或x>3}
(D){x|x -1或x
-1或x 3}
3}
[答案]C
[解析]因为集合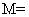
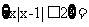
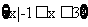 ,全集
,全集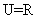 ,所以
,所以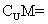
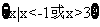 ,故选C.
,故选C.
[命题意图]本题考查集合的补集运算,属容易题.
(2)
已知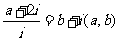
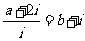 (a,b∈R),其中i为虚数单位,则a+b=
(a,b∈R),其中i为虚数单位,则a+b=
(A)-1 (B)1 (C)2 (D)3
[答案]B
[解析]由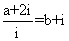 得
得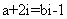 ,所以由复数相等的意义知:
,所以由复数相等的意义知: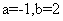 ,所以
,所以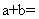 1,故选B.
1,故选B.
[命题意图]本题考查复数相等的意义、复数的基本运算,属保分题。
(3)在空间,下列命题正确的是
(A)平行直线的平行投影重合
(B)平行于同一直线的两个平面平行
(C)垂直于同一平面的两个平面平行
(D)垂直于同一平面的两条直线平行
[答案]D
[解析]由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
[命题意图]本题考查空间直线与平面的位置关系及线面垂直与平行的判定与性质,属基础题。
(4)设f(x)为定义在R上的奇函数,当x≥0时,f(x)=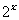 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=
(A) 3 (B) 1 (C)-1 (D)-3
[答案]D
[解析]因为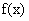 为定义在R上的奇函数,所以有
为定义在R上的奇函数,所以有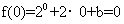 ,解得
,解得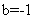 ,所以
,所以
当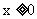 时,
时, 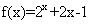 ,即
,即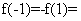
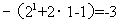 ,故选D.
,故选D.
[命题意图]本题考查函数的基本性质,熟练函数的基础知识是解答好本题的关键.
(5)已知随机变量Z服从正态分布N(0,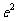 ),若P(Z>2)=0.023,则P(-2≤Z≤2)=
),若P(Z>2)=0.023,则P(-2≤Z≤2)=
(A)0.477 (B)0.625 (C)0.954 (D)0.977
[答案]C
[解析]因为随机变量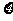 服从正态分布
服从正态分布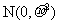 ,所以正态曲线关于直线
,所以正态曲线关于直线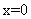 对称,又
对称,又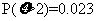 ,所以
,所以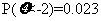 ,所以
,所以
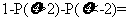
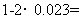 0.954,故选C.
0.954,故选C.
[命题意图]本题考查正态分布的基础知识,掌握其基础知识是解答好本题的关键.
(6)样本中共有五个个体,其值分别为a,0,1,2,3,,若该样本的平均值为1,则样本方差为
(A) 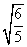 (B)
(B)
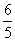 (C)
(C)
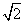 (D)2
(D)2
[答案]D
[解析]由题意知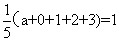 ,解得
,解得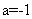 ,所以样本方差为
,所以样本方差为
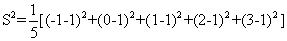 =2,故选D.
=2,故选D.
[命题意图]本题考查用样本的平均数、方差来估计总体的平均数、方差,属基础题,熟记样本的平均数、方差公式是解答好本题的关键.
(7)由曲线y= ,y=
,y=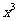 围成的封闭图形面积为
围成的封闭图形面积为
(A)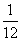 (B)
(B)
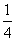 (C)
(C) 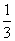 (D)
(D)
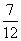
[答案]A
[解析]由题意得:所求封闭图形的面积为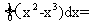
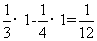 ,故选A。
,故选A。
[命题意图]本题考查定积分的基础知识,由定积分求曲线围成封闭图形的面积。
(8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
(A)36种 (B)42种 (C)48种 (D)54种
[答案]B
[解析]分两类:第一类:甲排在第一位,共有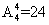 种排法;第二类:甲排在第二位,共有
种排法;第二类:甲排在第二位,共有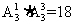 种排法,所以共有编排方案
种排法,所以共有编排方案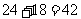 种,故选B。
种,故选B。
[命题意图]本题考查排列组合的基础知识,考查分类与分步计数原理。
(9)设{an}是等比数列,则“a1<a2<a3”是数列{an}是递增数列的
(A)充分而不必要条件 (B)必要而不充分条件、
(C)充分必要条件 (D)既不充分也不必要条件
[答案]C
[解析]若已知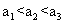 ,则设数列
,则设数列 的公比为
的公比为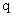 ,因为
,因为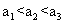 ,所以有
,所以有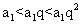 ,解得
,解得 且
且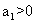 ,所以数列
,所以数列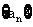 是递增数列;反之,若数列
是递增数列;反之,若数列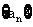 是递增数列,则公比
是递增数列,则公比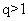 且
且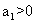 ,所以
,所以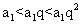 ,即
,即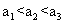 ,所以
,所以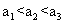 是数列
是数列 是递增数列的充分必要条件。
是递增数列的充分必要条件。
[命题意图]本题考查等比数列及充分必要条件的基础知识,属保分题。
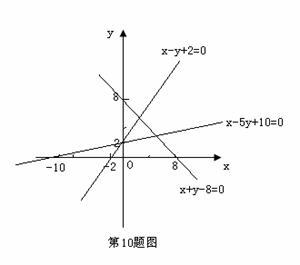 (10)设变量x、y满足约束条件
(10)设变量x、y满足约束条件 ,则目标函数z=3x-4y的最大值和最小值分别为
,则目标函数z=3x-4y的最大值和最小值分别为
(A)3,-11 (B) -3, -11
(C)11, -3 (D)11,3
[答案]A
[解析]画出平面区域如图所示:
可知当直线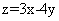 平移到点(5,3)时,目标函数
平移到点(5,3)时,目标函数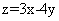 取得最大值3;当直线
取得最大值3;当直线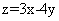 平移到点(3,5)时,目标函数
平移到点(3,5)时,目标函数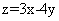 取得最小值-11,故选A。
取得最小值-11,故选A。
[命题意图]本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数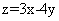 的几何意义是解答好本题的关键。
的几何意义是解答好本题的关键。
(11)函数y=2x - 的图像大致是
的图像大致是
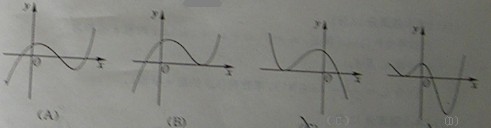
[答案]A
[解析]因为当x=2或4时,2x - =0,所以排除B、C;当x=-2时,2x -
=0,所以排除B、C;当x=-2时,2x - =
=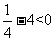 ,故排除D,所以选A。
,故排除D,所以选A。
[命题意图]本题考查函数的图象,考查同学们对函数基础知识的把握程度以及数形结合的思维能力。
(12)定义平面向量之间的一种运算“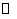 ”如下,对任意的
”如下,对任意的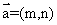 ,
,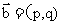 ,令
,令
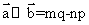 ,下面说法错误的是( )
,下面说法错误的是( )
A.若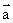 与
与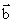 共线,则
共线,则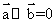 B.
B.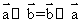
C.对任意的 ,有
,有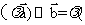
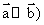 D.
D. 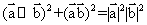
[答案]B
[解析]若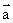 与
与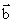 共线,则有
共线,则有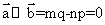 ,故A正确;因为
,故A正确;因为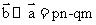 ,而
,而
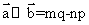 ,所以有
,所以有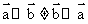 ,故选项B错误,故选B。
,故选项B错误,故选B。
[命题意图]本题在平面向量的基础上,加以创新,属创新题型,考查平面向量的基础知识以及分析问题、解决问题的能力。
22. (本小题满分12分)已知椭圆
(本小题满分12分)已知椭圆 ,直线
,直线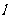 与椭圆交于
与椭圆交于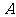 、
、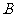 两点,
两点,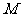 是线段
是线段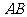 的中点,连接
的中点,连接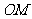 并延长交椭圆于点
并延长交椭圆于点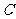 。
。
(Ⅰ)设直线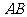 与直线
与直线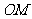 的斜率分别为
的斜率分别为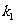 、
、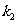 ,且
,且 ,求椭圆的离心率的取值范围。
,求椭圆的离心率的取值范围。
(Ⅱ)若直线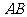 经过椭圆的右焦点
经过椭圆的右焦点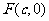 ,且四边形
,且四边形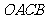 是面积为
是面积为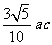 的平行四边形,求直线
的平行四边形,求直线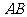 倾斜角的大小。
倾斜角的大小。
冀州中学2009-2010学年高三年级第一次仿真考试
21. (本小题满分12分)
已知函数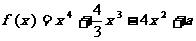
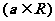
(Ⅰ)求函数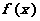 的极大值;
的极大值;
(Ⅱ)当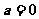 时,求函数
时,求函数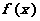 的值域;
的值域;
(Ⅲ)已知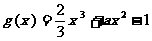 ,当
,当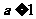 时,
时,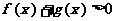 恒成立,求
恒成立,求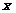 的取值范围.
的取值范围.
20.(本小题满分12分)如图,四棱锥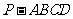 的底面
的底面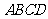 为一直角梯形,其中
为一直角梯形,其中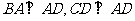 ,
,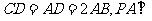 底面
底面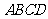 ,
,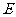 是
是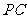 的中点.
的中点.
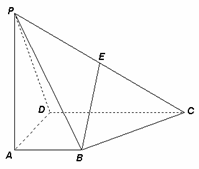 (1)求证:
(1)求证: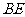 //平面
//平面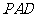 ;
;
(2)若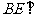 平面
平面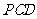 ,
,
①求异面直线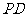 与
与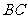 所成角的余弦值;
所成角的余弦值;
②求二面角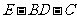 的余弦值
的余弦值
18.(本小题满分12分)
在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球5个,白球3个,蓝球2个.现从中任取出一球确定颜色后放回盒子里,再取下一个球.重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球. 求: (1)最多取两次就结束的概率;
(2)整个过程中恰好取到2个白球的概率; 19. (本小题满分12分)
已知等差数列{an}的首项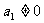 ,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4
(1)若a1=2,设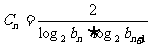 ,求数列{cn}的前n项的和Tn;
,求数列{cn}的前n项的和Tn;
(2)在(1)的条件下,若有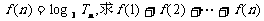 的最大值.
的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com