
7. 若x>0, y>0,且x+y 4,则下列不等式中恒成立的是
( )
4,则下列不等式中恒成立的是
( )
A. B.
B.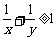 C.
C.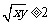 D.
D.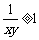
6. 若a, b, c∈R,且ab+bc+ca=1, 则下列不等式成立的是 ( )
A.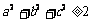 B.
B.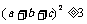
C.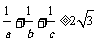 D.
D.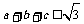
5. 若x, y是正数,且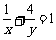 ,则xy有 ( )
,则xy有 ( )
A.最大值16 B.最小值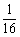 C.最小值16 D.最大值
C.最小值16 D.最大值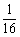
4. 设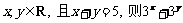 的最小值是(
)
的最小值是(
)
A. 10
B. 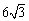 C.
C. 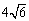 D.
D. 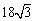
3. 设x>0,则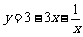 的最大值为
( )
的最大值为
( )
A.3 B. C.
C.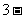
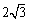 D.-1
D.-1
2. 若 且
且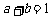 ,则下列四个数中最大的是 ( )
,则下列四个数中最大的是 ( )
A.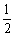 B.
B.
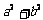 C.2ab D.a
C.2ab D.a
1. 若
 ,下列不等式恒成立的是 (
)
,下列不等式恒成立的是 (
)
A.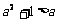 B.
B.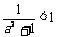 C.
C.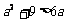 D.
D.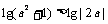
9.若把满足二元二次不等式(组)的平面区域叫做二次平面域.
(1)画出9x2-16y2+144≤0对应的二次平面域;
(2)求x2+y2的最小值;
(3)求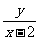 的取值范围.
的取值范围.
 必修5
第3章 不等式
必修5
第3章 不等式
§3.4基本不等式
重难点:了解基本不等式的证明过程;会用基本不等式解决简单的最大(小)值问题.
考纲要求:①了解基本不等式的证明过程.
②会用基本不等式解决简单的最大(小)值问题.
经典例题:若a,b,c都是小于1的正数,求证: ,
,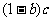 ,
,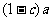 不可能同时大于
不可能同时大于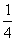 .
.
8.给出的平面区域是△ABC内部及边界(如下图),若目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,求a的值及z的最大值.

7.已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com